Bivariate analyse uitvoeren in r (met voorbeelden)

De term bivariate analyse verwijst naar de analyse van twee variabelen. U kunt dit onthouden omdat het voorvoegsel “bi” “twee” betekent.

Het doel van bivariate analyse is om de relatie tussen twee variabelen te begrijpen

Er zijn drie veelgebruikte manieren om bivariate analyses uit te voeren:

1. Puntenwolken

2. Correlatiecoëfficiënten

3. Eenvoudige lineaire regressie

Het volgende voorbeeld laat zien hoe u elk van deze soorten bivariate analyses kunt uitvoeren met behulp van de volgende dataset die informatie over twee variabelen bevat: (1) Uren besteed aan studeren en (2) Toetsscores behaald door 20 verschillende studenten:

 #create data frame
df <- data. frame (hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                         3, 4, 4, 5, 5, 6, 6, 6, 7, 8),
                 score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                         80, 88, 85, 90, 92, 94, 94, 88, 91, 96))

#view first six rows of data frame
head(df)

  hours score
1 1 75
2 1 66
3 1 68
4 2 74
5 2 78
6 2 72

1. Puntenwolken

We kunnen de volgende syntaxis gebruiken om een spreidingsdiagram te maken van de bestudeerde uren versus het examencijfer in R:

 #create scatterplot of hours studied vs. exam score
plot(df$hours, df$score, pch= 16 , col=' steelblue ',
     main=' Hours Studied vs. Exam Score ',
     xlab=' Hours Studied ', ylab=' Exam Score ')

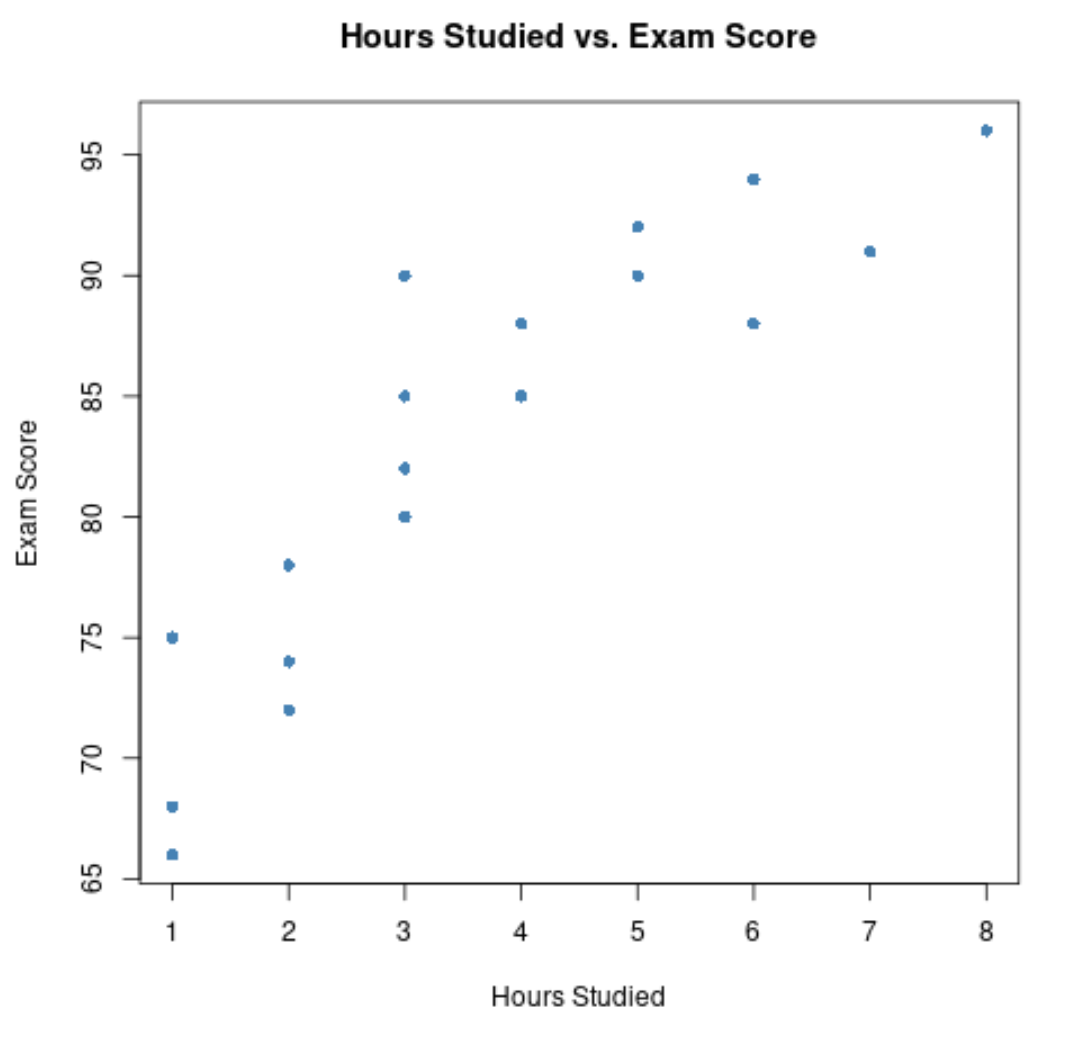
Op de x-as staan de bestudeerde uren en op de y-as het behaalde cijfer voor het examen.

Uit de grafiek blijkt dat er een positief verband bestaat tussen beide variabelen: naarmate het aantal studie-uren toeneemt, stijgen ook de examenscores.

2. Correlatiecoëfficiënten

Een Pearson-correlatiecoëfficiënt is een manier om de lineaire relatie tussen twee variabelen te kwantificeren.

We kunnen de functie cor() in R gebruiken om de Pearson-correlatiecoëfficiënt tussen twee variabelen te berekenen:

 #calculate correlation between hours studied and exam score received
cor(df$hours, df$score)

[1] 0.891306

De correlatiecoëfficiënt blijkt 0,891 te zijn.

Deze waarde ligt dicht bij 1, wat wijst op een sterke positieve correlatie tussen het aantal gestudeerde uren en het examencijfer.

3. Eenvoudige lineaire regressie

Eenvoudige lineaire regressie is een statistische methode die we kunnen gebruiken om de vergelijking van de lijn te vinden die het beste bij een reeks gegevens past, die we vervolgens kunnen gebruiken om de exacte relatie tussen twee variabelen te begrijpen.

We kunnen de functie lm() in R gebruiken om een eenvoudig lineair regressiemodel uit te voeren voor de bestudeerde uren en ontvangen examenresultaten:

 #fit simple linear regression model
fit <- lm(score ~ hours, data=df)

#view summary of model
summary(fit)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-6,920 -3,927 1,309 1,903 9,385 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 69.0734 1.9651 35.15 < 2nd-16 ***
hours 3.8471 0.4613 8.34 1.35e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.171 on 18 degrees of freedom
Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 
F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07

De gepaste regressievergelijking blijkt te zijn:

Examenscore = 69.0734 + 3.8471*(uren gestudeerd)

Dit vertelt ons dat elk extra uur dat wordt gestudeerd, gepaard gaat met een gemiddelde stijging van 3,8471 in de examenscore.

We kunnen de gepaste regressievergelijking ook gebruiken om de score te voorspellen die een student zal behalen op basis van het totale aantal bestudeerde uren.

Een student die bijvoorbeeld 3 uur studeert, zou een score van 81,6147 moeten behalen:

• Examenscore = 69.0734 + 3.8471*(uren gestudeerd)
• Examenscore = 69,0734 + 3,8471*(3)
• Examenresultaat = 81,6147

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over bivariate analyse:

Een inleiding tot bivariate analyse
5 voorbeelden van bivariate gegevens in het echte leven
Een inleiding tot eenvoudige lineaire regressie