Hoe een bivariate normale verdeling in r te simuleren en uit te zetten

In de statistiek volgen twee variabelen een bivariate normale verdeling als ze bij elkaar opgeteld een normale verdeling hebben.

In deze tutorial wordt uitgelegd hoe u de volgende taken in R uitvoert:

• Simuleer een bivariate normale verdeling
• Teken een bivariate normale verdeling met behulp van een contourplot (2D-plot)
• Teken een bivariate normale verdeling met behulp van een oppervlakteplot (3D-plot)

Laten we gaan!

Voorbeeld 1: Simuleer een bivariate normale verdeling in R

De eenvoudigste manier om een bivariate normale verdeling in R te simuleren is door de functie mvrnorm() uit het MASS- pakket te gebruiken.

De volgende code laat zien hoe u deze functie kunt gebruiken om in de praktijk een bivariate normale verdeling te simuleren:

 library (MASS)

#make this example reproducible
set. seed ( 0 )

#simulate bivariate normal distribution
bivariate_data <- as. data . frame (mvrnorm(n= 100 ,
                                        mu=c(0, 0),
                                        Sigma=matrix(c(5, 3, 4, 4), ncol= 2 )))

#view first six rows of bivariate dataset
head(bivariate_data)

           V1 V2
1 -2.03600343 -2.9623059
2 0.07719131 1.2948982
3 -3.26729701 -1.7928069
4 -2.62985132 -2.3015471
5 -1.75126215 0.3056698
6 3.67698436 2.2020238

Dit is wat elk argument voor de functie mvrnorm() doet:

• n : Definieert de steekproefomvang
• mu : Definieert het gemiddelde van elke variabele
• Sigma : definieert de covariantiematrix van de twee variabelen

Het eindresultaat is een dataframe met twee variabelen die bij elkaar opgeteld een normale verdeling volgen.

Voorbeeld 2: Een bivariate normale verdeling uitzetten

De eenvoudigste manier om een bivariate normale verdeling in R te plotten is door de functies in het mnormt() -pakket te gebruiken.

We kunnen bijvoorbeeld de functie contour() van dit pakket gebruiken om een contourplot te maken, dat een 2D-visualisatie biedt van de bivariate normale verdeling:

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create contour plot
contour(x, y, z)

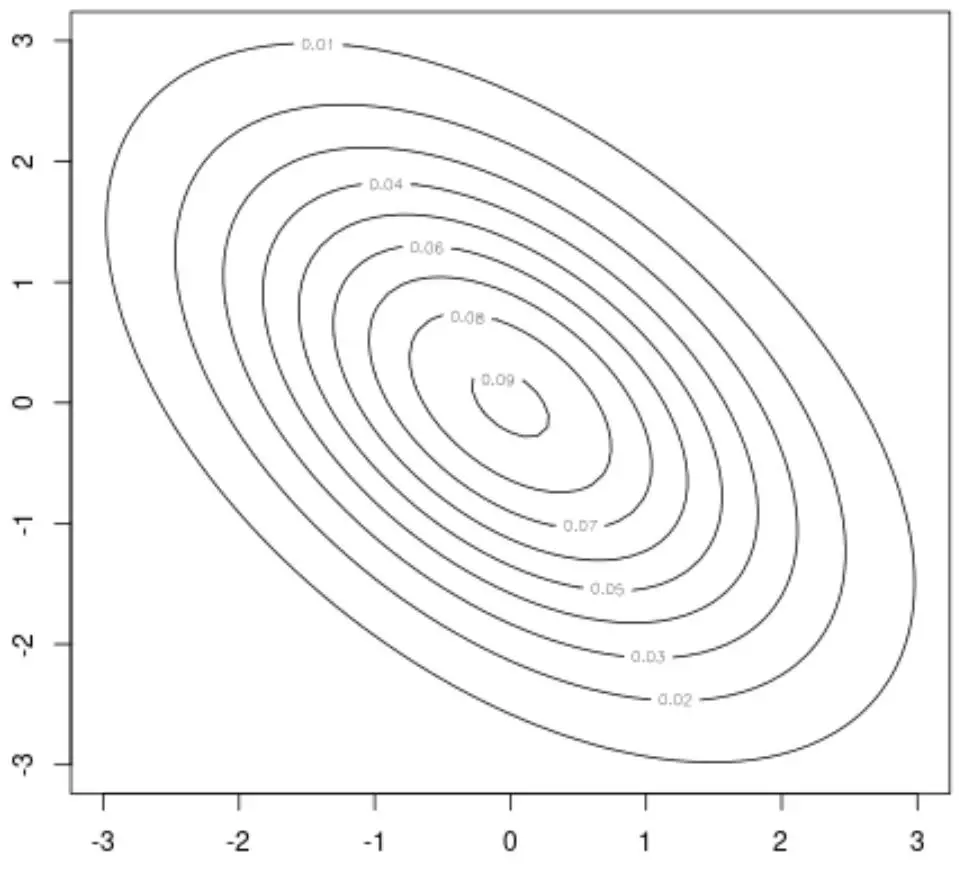
We kunnen ook de functie persp() gebruiken om een oppervlakteplot te maken, dat een 3D-visualisatie biedt van de bivariate normale verdeling:

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create surface plot
persp(x, y, z, theta= -30 , phi= 25 , expand= 0.6 , ticktype=' detailed ')

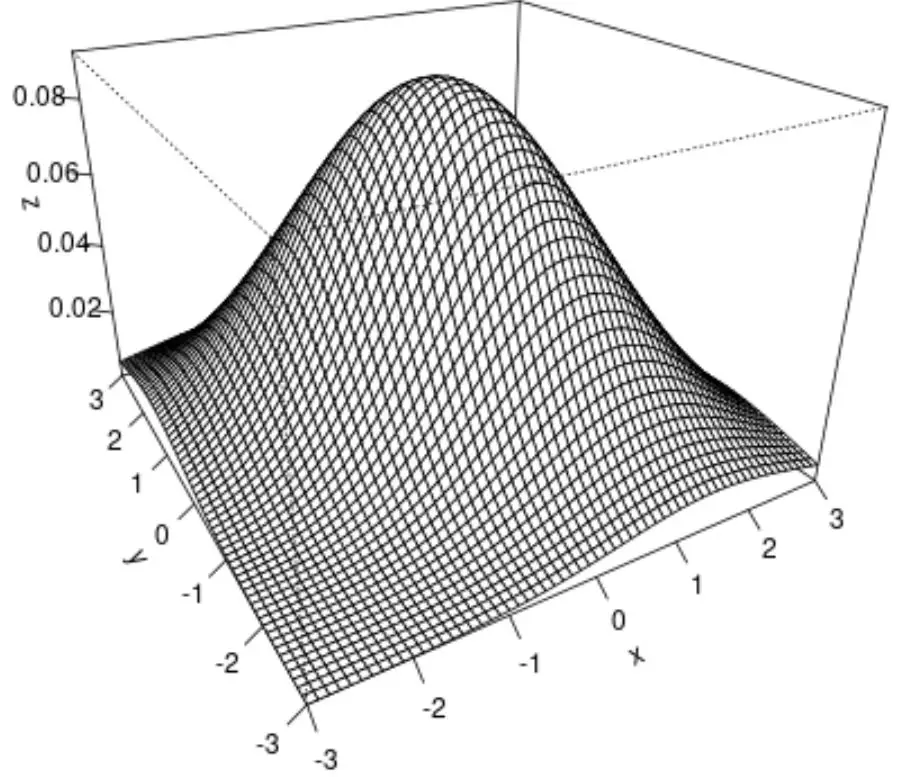
Dit is wat elk argument voor de functie persp() doet:

• theta, phi : Stelt de kijkrichtingshoeken in.
• expand : Bepaalt de grootte van de z-as.
• ticktype : Bepaalt de weergave van vinkjes op de assen.

Het eindresultaat is een 3D-oppervlaktegrafiek van de bivariate normale verdeling.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere kansverdelingen in R kunt gebruiken:

Hoe de normale verdeling in R te gebruiken
Hoe binominale verdeling te gebruiken in R
Hoe de Poisson-verdeling in R te gebruiken
Hoe multinomiale distributie te gebruiken in R