Hoe de test van white in sas uit te voeren

De test van White wordt gebruikt om te bepalen of heteroscedasticiteit aanwezig is in een regressiemodel.

Heteroscedasticiteit verwijst naar de ongelijke spreiding van residuen op verschillende niveaus van eenresponsvariabele in een regressiemodel, wat in strijd is met een van de belangrijkste aannames van lineaire regressie dat residuen gelijkmatig verspreid zijn op elk niveau van de responsvariabele.

In deze zelfstudie wordt uitgelegd hoe u de White-test in SAS uitvoert om te bepalen of heteroskedasticiteit al dan niet een probleem is in een bepaald regressiemodel.

Voorbeeld: Witte test in SAS

Stel dat we een meervoudig lineair regressiemodel willen toepassen dat het aantal uren dat aan studeren wordt besteed en het aantal afgelegde oefenexamens gebruikt om het eindexamencijfer van studenten te voorspellen:

Examenscore = β ₀ + β ₁ (uren) + β ₂ (voorbereidende examens)

Eerst gebruiken we de volgende code om een dataset te maken met deze informatie voor 20 studenten:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 90
5 4 90
3 4 82
4 4 85
6 5 90
2 1 83
1 0 62
2 1 76
;
run ;

/*view dataset*/
proc print data =exam_data; 

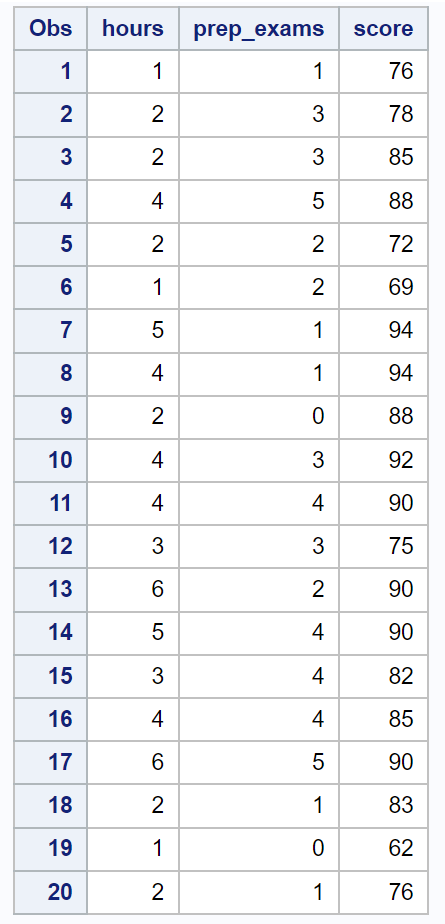
Vervolgens zullen we proc reg gebruiken om aan dit meervoudige lineaire regressiemodel te voldoen, evenals de spec- optie om White’s test voor heteroscedasticiteit uit te voeren:

 /*fit regression model and perform White's test*/
proc reg data =exam_data;
    model score = hours prep_exams / spec ;
run ;
quit ; 

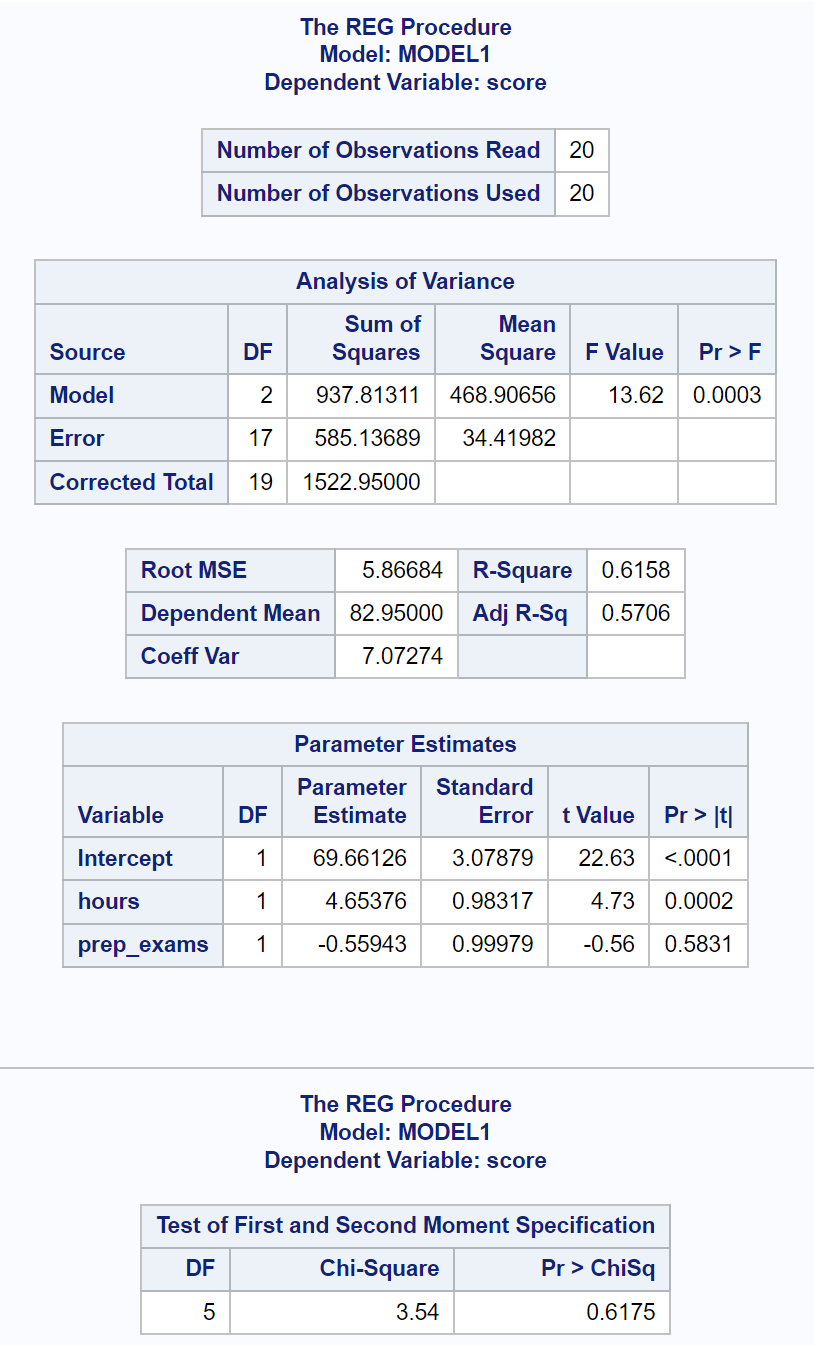
De laatste resultatentabel toont de resultaten van White’s test.

Uit deze tabel kunnen we zien dat de Chi-kwadraat-teststatistiek 3,54 is en de overeenkomstige p-waarde 0,6175 .

De Witte test gebruikt de volgende nul- en alternatieve hypothesen:

• Nul (H ₀ ) : Er is geen heteroskedasticiteit aanwezig.
• Alternatief ( _HA ): Er is heteroskedasticiteit aanwezig.

Omdat de p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen.

Dit betekent dat we niet voldoende bewijs hebben om te beweren dat heteroscedasticiteit aanwezig is in het regressiemodel.

Het is daarom mogelijk om de standaardfouten van de coëfficiëntschattingen in de regressieoverzichtstabel veilig te interpreteren.

Wat nu te doen

Als u er niet in slaagt de nulhypothese van White’s test te verwerpen, is er geen sprake van heteroscedasticiteit en kunt u doorgaan met het interpreteren van het resultaat van de oorspronkelijke regressie.

Als u echter de nulhypothese verwerpt, betekent dit dat er heteroskedasticiteit aanwezig is in de gegevens. In dit geval zijn de standaardfouten die in de regressie-uitvoertabel worden weergegeven mogelijk onbetrouwbaar.

Er zijn verschillende veelvoorkomende manieren om dit probleem op te lossen, waaronder:

1. Transformeer de responsvariabele. U kunt proberen een transformatie uit te voeren op de responsvariabele.

U kunt bijvoorbeeld de logboekresponsvariabele gebruiken in plaats van de oorspronkelijke responsvariabele.

Over het algemeen is het nemen van de log van de responsvariabele een effectieve manier om heteroskedasticiteit te laten verdwijnen.

Een andere veel voorkomende transformatie is het gebruik van de vierkantswortel van de responsvariabele.

2. Gebruik gewogen regressie. Dit type regressie kent een gewicht toe aan elk gegevenspunt op basis van de variantie van de aangepaste waarde.

Dit geeft kleine gewichten aan datapunten met grotere varianties, waardoor hun resterende kwadraten kleiner worden.

Wanneer de juiste gewichten worden gebruikt, kan dit het probleem van heteroskedasticiteit elimineren.