Een bonferroni-correctie uitvoeren in excel

Een Bonferroni-correctie verwijst naar het proces van het aanpassen van het alfa(α)-niveau voor een familie van statistische tests om de waarschijnlijkheid van het maken van een Type I-fout te beheersen.

De formule voor een Bonferroni-correctie is als volgt:

α _nieuw = α _origineel / n

Goud:

• _originele α: het oorspronkelijke α-niveau
• n: Het totale aantal uitgevoerde vergelijkingen of tests

Als we bijvoorbeeld drie statistische tests tegelijk uitvoeren en voor elke test α = 0,05 willen gebruiken, vertelt de Bonferroni-correctie ons dat we α _new = 0,01667 moeten gebruiken.

_nieuw α = _origineel α / n = 0,05 / 3 = 0,01667

We moeten de nulhypothese van elke individuele test dus alleen verwerpen als de p-waarde van de test kleiner is dan 0,01667.

Dit type correctie wordt vaak uitgevoerd in post-hoc tests na een ANOVA, wanneer we meerdere groepsgemiddelden tegelijkertijd willen vergelijken.

Het volgende stapsgewijze voorbeeld laat zien hoe u een Bonferroni-correctie uitvoert na een eenrichtings-ANOVA in Excel.

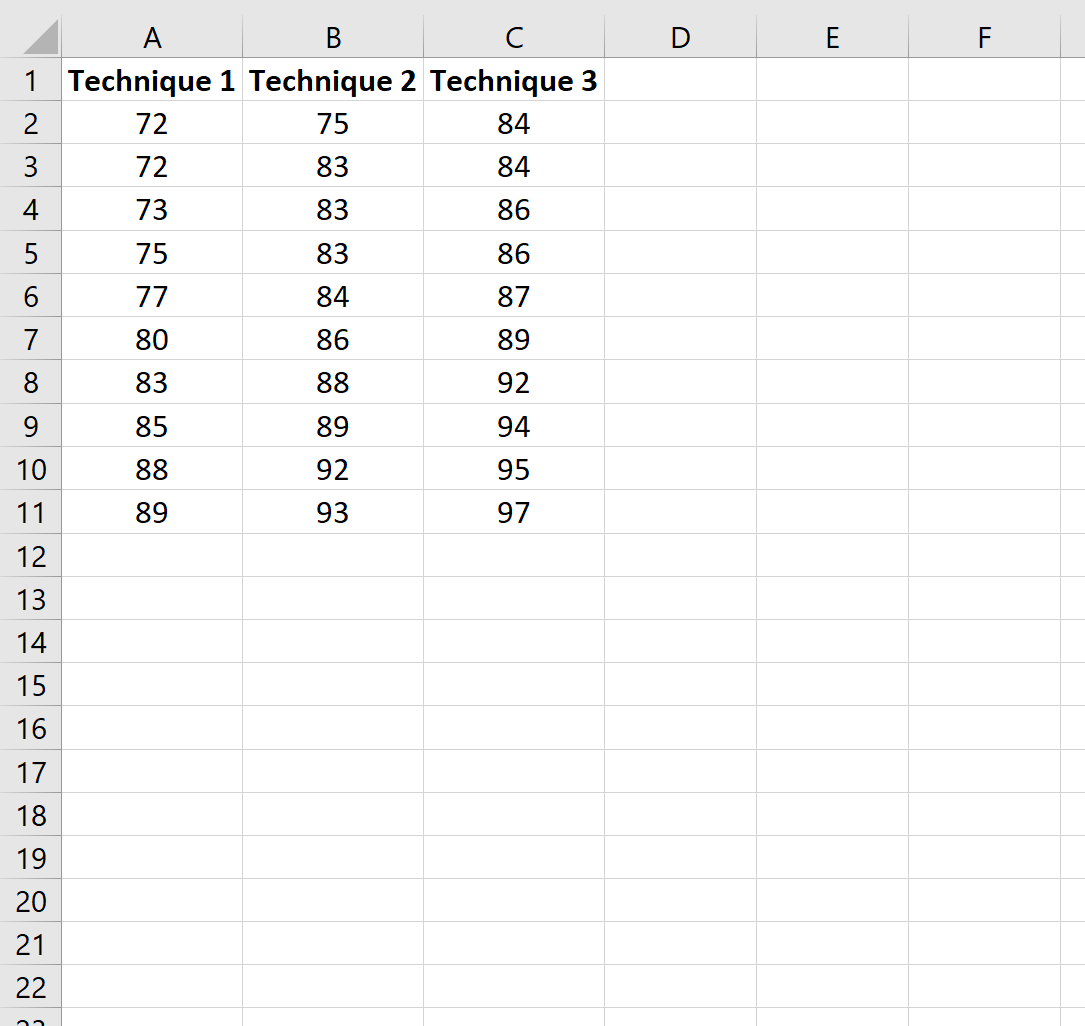
Stap 1: Creëer de gegevens

Laten we eerst een nep-dataset maken die de resultaten laat zien van studenten die een van de drie verschillende studietechnieken hebben gebruikt om zich voor te bereiden op het examen:

Stap 2: Voer eenrichtings-ANOVA uit

Laten we vervolgens een eenrichtings-ANOVA uitvoeren om te bepalen of de gemiddelde examenscores voor de drie groepen gelijk zijn.

Markeer eerst alle gegevens, inclusief de kolomkoppen:

Klik vervolgens op het tabblad Gegevens op het bovenste lint en klik vervolgens op Gegevensanalyse :

Als deze optie niet beschikbaar is, moet u eerst Analysis ToolPak laden .

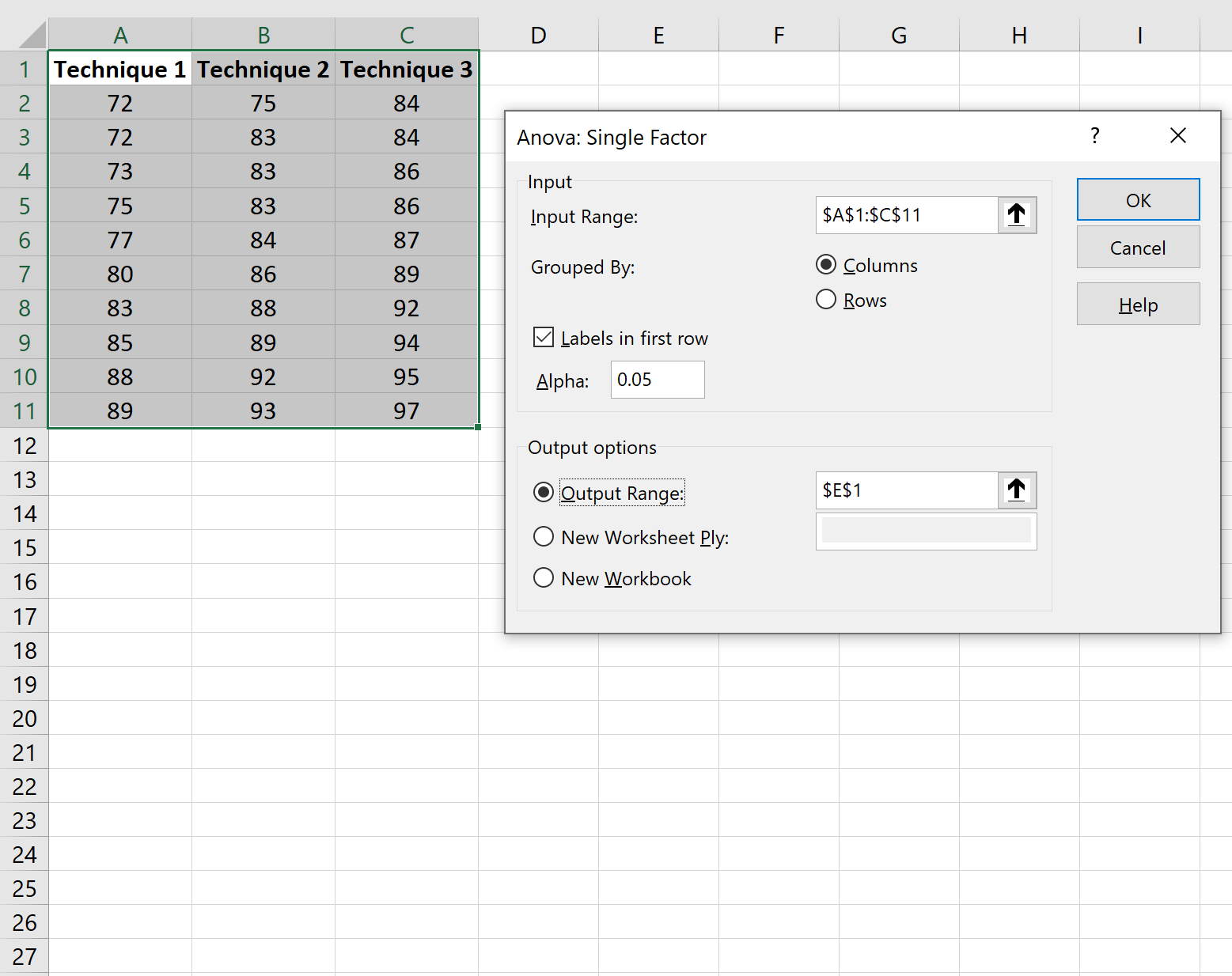
In het venster dat verschijnt, klikt u op Anova: Single Factor en vervolgens op OK .

Vul de volgende gegevens in en klik vervolgens op OK :

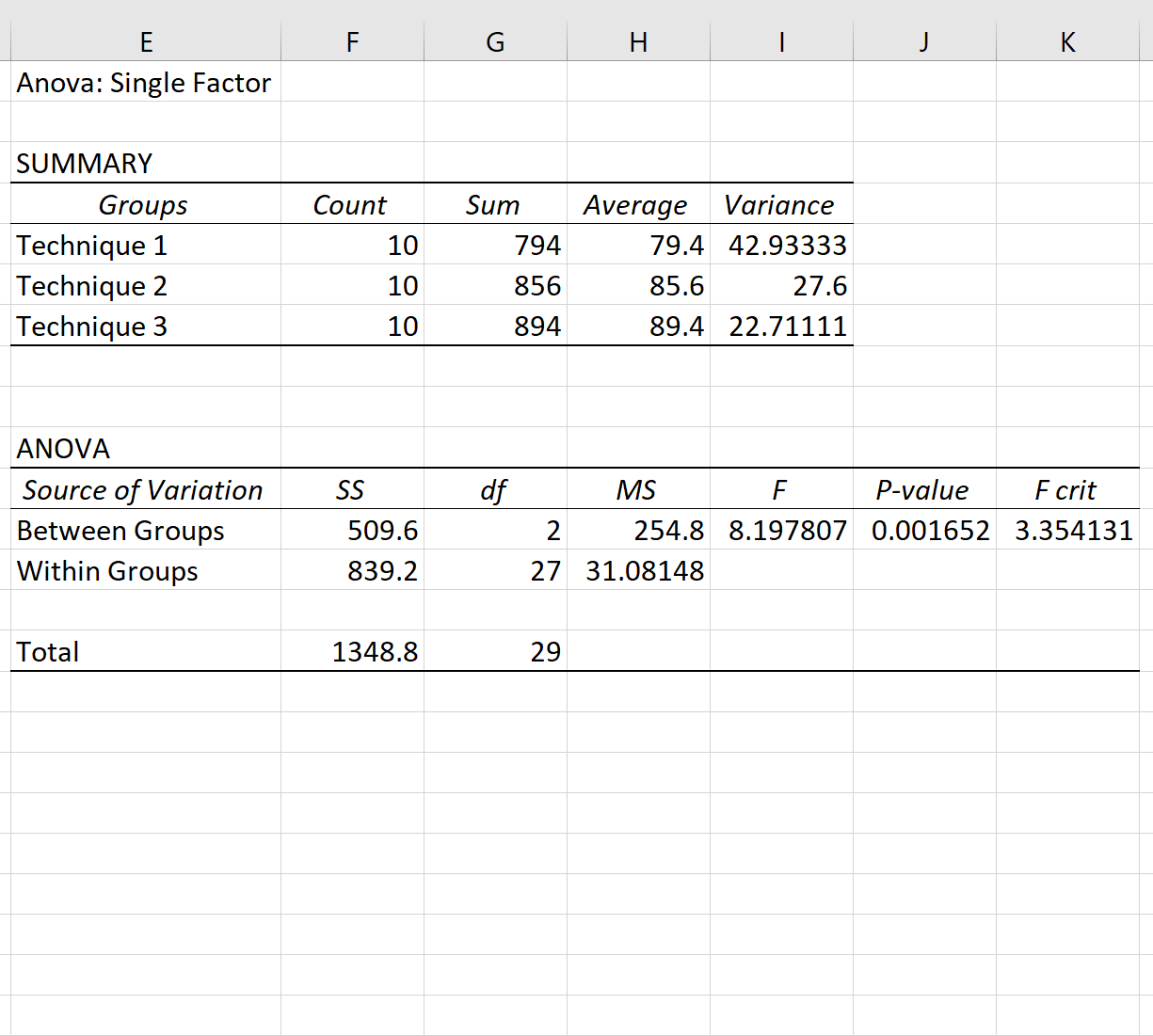
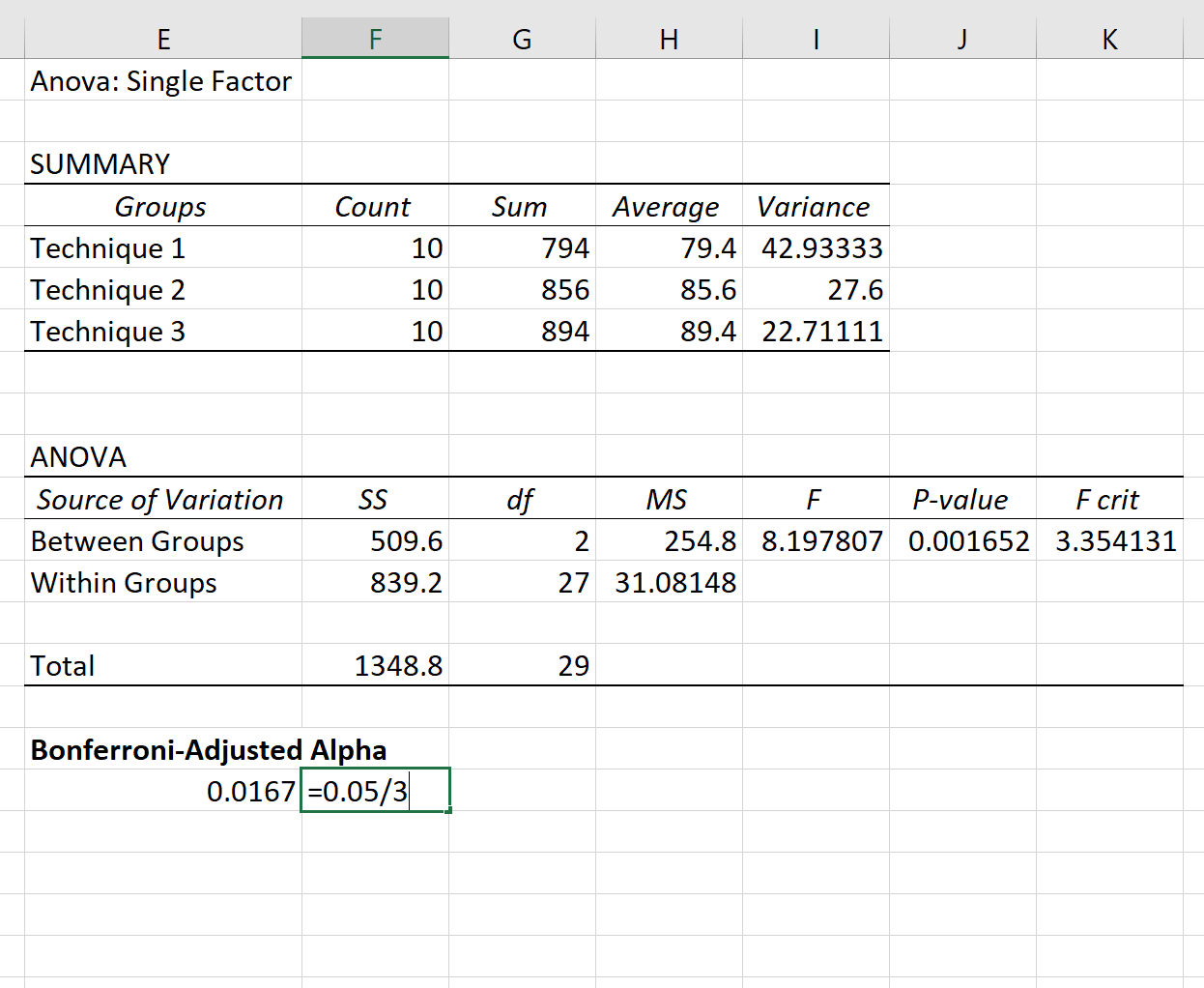
De eenrichtings-ANOVA-resultaten verschijnen automatisch:

Bedenk dat een eenrichtings-ANOVA de volgende nul- en alternatieve hypothesen heeft:

• H ₀ (nulhypothese): alle groepsgemiddelden zijn gelijk.
• _HA (alternatieve hypothese): Ten minste één groepsgemiddelde is verschillend   rest.

Omdat de p-waarde in de ANOVA-tabel (0,001652) kleiner is dan 0,05, hebben we voldoende bewijs om de nulhypothese te verwerpen. Met andere woorden: de gemiddelde examenscores tussen de drie groepen zijn niet gelijk.

Vervolgens kunnen we met behulp van een Bonferroni-correctie verschillende vergelijkingen maken tussen de drie groepen om precies te zien welke groepsgemiddelden verschillend zijn.

Stap 3: Voer meerdere vergelijkingen uit met behulp van een Bonferroni-correctie

Met behulp van een Bonferroni-correctie kunnen we het aangepaste alfaniveau als volgt berekenen:

α _nieuw = α _origineel / n

In ons voorbeeld zullen we de volgende drie vergelijkingen uitvoeren:

• Techniek 1 versus Techniek 2
• Techniek 1 versus Techniek 3
• Techniek 2 versus Techniek 3

Omdat we voor elke test α = .05 willen gebruiken, vertelt de Bonferroni-correctie ons dat we α _new = .0167 moeten gebruiken.

Vervolgens zullen we een t-test gebruiken om de gemiddelden tussen elke groep te vergelijken. In Excel kunt u de volgende syntaxis gebruiken:

=TTEST(Tabel1, Tabel2, wachtrijen=2, type=2)

Goud:

• Array1: de eerste gegevensarray
• Array2: de tweede gegevensarray
• staarten: het aantal staarten in de test. We zullen “2” gebruiken om een tweezijdige test aan te duiden.
• type: het type t-test dat moet worden uitgevoerd. We zullen „2“ gebruiken om een t-toets met gelijke varianties aan te geven.

De volgende schermafbeelding laat zien hoe u elke t-test uitvoert:

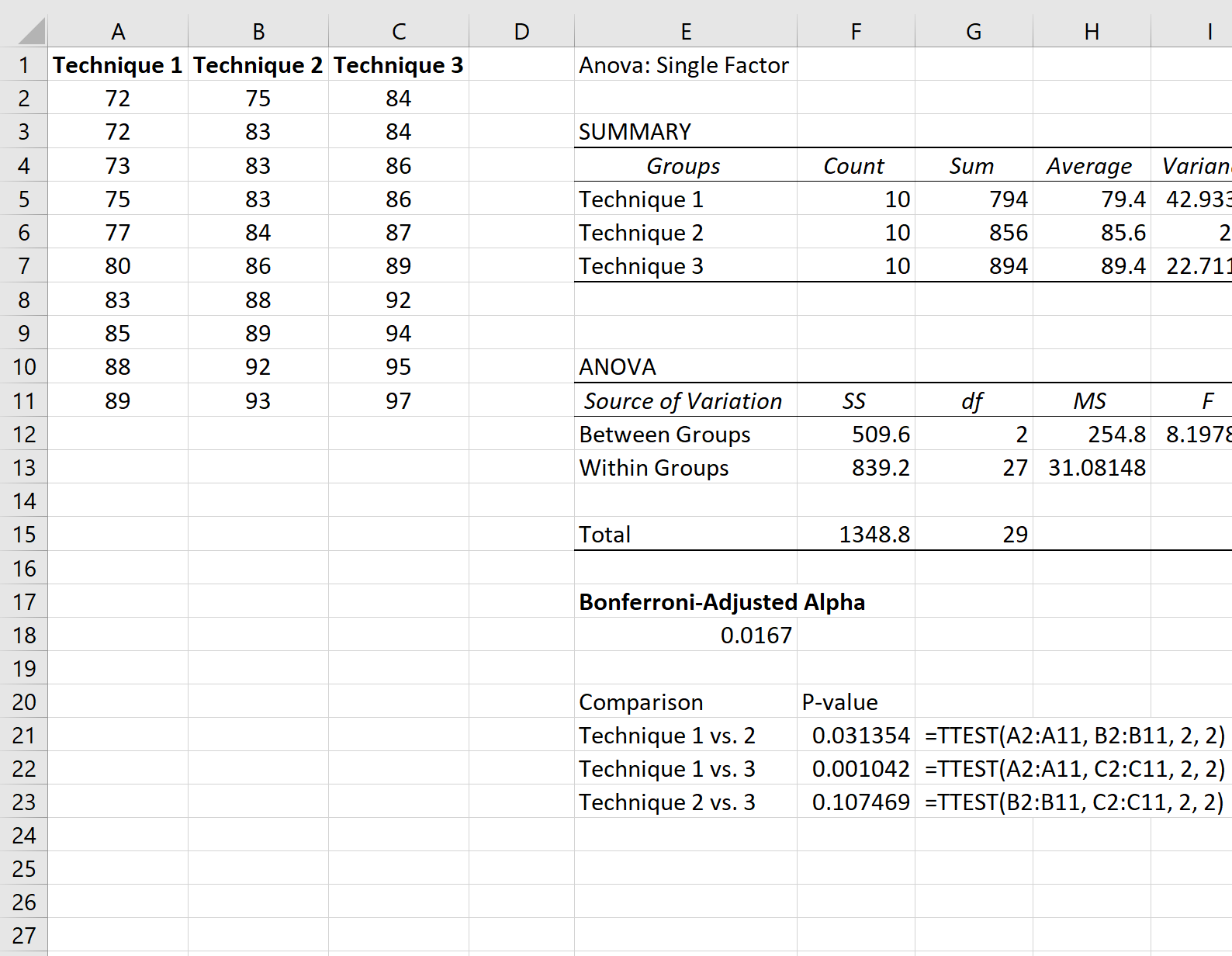
De enige p-waarde onder het door Bonferroni aangepaste alfaniveau komt uit de vergelijking tussen techniek 1 en techniek 2, die een p-waarde had van 0,001042 .

We zouden dus kunnen concluderen dat alleen het statistisch significante verschil in gemiddelde examenscores bestond tussen Techniek 1 en Techniek 2.

Aanvullende bronnen

Wat is het foutenpercentage per gezin?
De Bonferroni-correctie: definitie en voorbeeld
Bonferroni-correctiecalculator