Boomdiagram

In dit artikel wordt uitgelegd wat een boomdiagram is en hoe deze wordt gemaakt. Zo vindt u voorbeelden van boomstructuren, de voordelen van dit soort diagrammen en bovendien een oefening die stap voor stap wordt opgelost.

Wat is een boom?

Een boomdiagram , ook wel waarschijnlijkheidsboom genoemd, is een grafische weergave van alle mogelijke uitkomsten van een experiment, samen met hun kansen.

Er wordt dus een boomdiagram gebruikt om alle mogelijke uitkomsten in een steekproefruimte in kaart te brengen en hun kansen te berekenen.

Een boomdiagram wordt zo gemaakt dat elk resultaat ( knooppunt ) vertakt in nieuwe mogelijke resultaten ( vertakkingen ) totdat de uiteindelijke resultaten zijn bereikt.

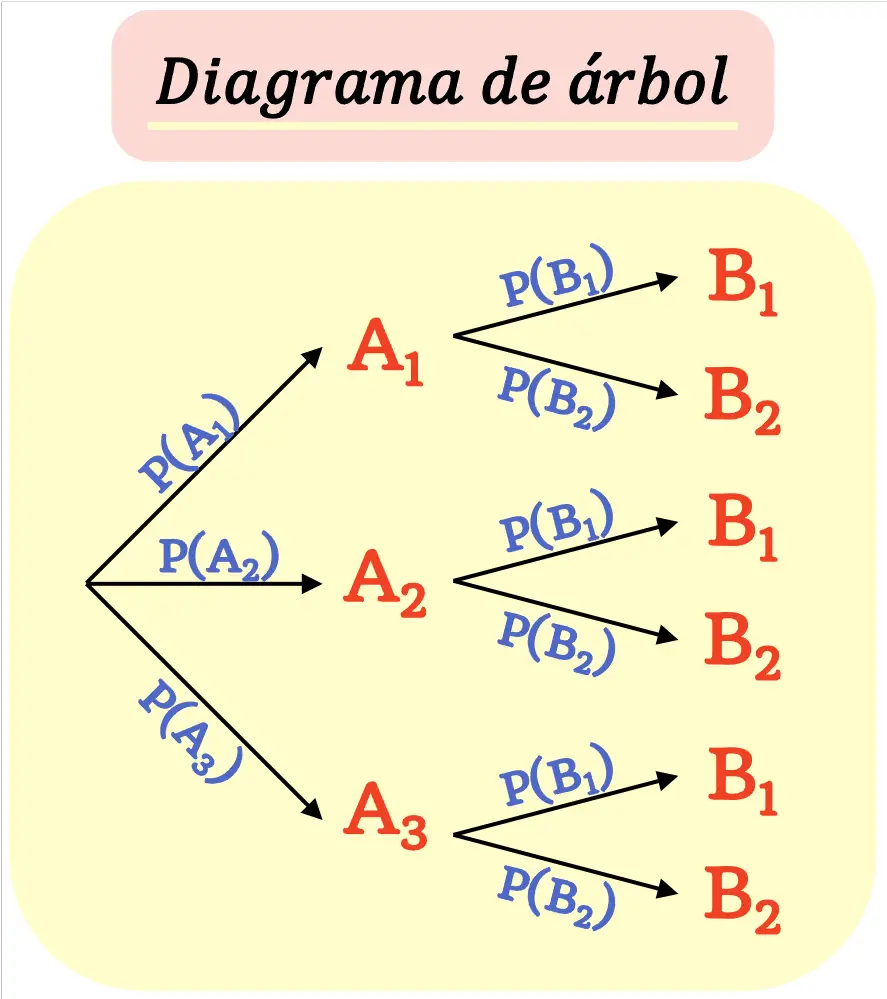
Houd er rekening mee dat de som van de kansen van alle takken die uit een knooppunt komen gelijk moet zijn aan 1.

Hoe maak je een boomdiagram

Om een boom te maken, moet u de volgende stappen volgen:

1. De eerste stap bij het maken van een boomdiagram is het tekenen van een vertakking voor elke mogelijke uitkomst. Dit zullen de takken van de eerste generatie zijn.
2. Vervolgens wordt de waarschijnlijkheid die bij elke gebeurtenis hoort, toegevoegd aan de overeenkomstige tak.
3. Het einde van elke tak van de eerste generatie is een knooppunt van waaruit takken van volgende mogelijke gebeurtenissen moeten worden weergegeven.
4. Net als bij de eerste takken moeten we de waarschijnlijkheden van de weergegeven gebeurtenissen optellen.
5. Herhaal stap 3 en 4 totdat je de laatste knooppunten bereikt, d.w.z. de mogelijke eindes van het experiment.

Merk op dat het aantal vestigingen op één niveau niet noodzakelijkerwijs gelijk hoeft te zijn aan het aantal vestigingen op een ander niveau. Op dezelfde manier kan het aantal vertakkingen dat voortkomt uit een mogelijke uitkomst zelfs binnen hetzelfde niveau variëren.

Boom voorbeeld

Nu we de definitie en theorie kennen van het maken van een boomdiagram, gaan we stap voor stap naar een voorbeeld uit de praktijk kijken om het concept beter te begrijpen.

• Construeer de waarschijnlijkheidsboom van het opgooien van drie onafhankelijke munten. Bepaal vervolgens de kans dat je kop krijgt bij alle drie de worpen.

Bij lottrekking zijn er slechts twee mogelijke resultaten: we kunnen kop of munt krijgen. Daarom is de kans op kop of munt bij het opgooien van een munt:

Zodra we de waarschijnlijkheden van mogelijke uitkomsten kennen, gaan we verder met het weergeven van het boomdiagram.

Omdat het opgooien van munten onafhankelijk is, zal de kans op kop of munt bij elke worp altijd hetzelfde zijn. Om de boom te kunnen bouwen, moeten daarom bij elke worp twee takken (kop en staart) met dezelfde waarschijnlijkheid worden weergegeven.

En als we eenmaal de boom hebben gemaakt, hoeven we alleen nog maar de kans te bepalen dat we de drie toss krijgen.

Daarom moeten we in dit geval alle kansen om kop te krijgen vermenigvuldigen, omdat dit de kansen zijn van het pad dat ons naar het gewenste resultaat leidt.

De kans op kop bij de drie opgooien wordt dus als volgt berekend:

Kortom, de kans dat je drie keer op rij kop krijgt is 12,5%.

Boomoefening opgelost

In een dorp zijn maar 3 crèches: 60% van de kinderen gaat naar crèche A, 30% naar crèche B en 10% naar crèche C. Bovendien is in de drie crèches 55% van de bevolking meisje. Bouw de boom en bereken de volgende kansen:

• Waarschijnlijkheid dat wanneer een kind willekeurig wordt geselecteerd, het een meisje is van kinderdagverblijf B.
• De waarschijnlijkheid dat wanneer een kind willekeurig wordt geselecteerd uit een kinderdagverblijf, het een jongen zal zijn.

Merk op dat als het aandeel meisjes in alle kinderdagverblijven 55% is, het percentage jongens wordt berekend door simpelweg 1 min 0,55 af te trekken:

Nu we alle kansen kennen, kunnen we de waarschijnlijkheidsboom met alle mogelijkheden maken:

De kans op het willekeurig selecteren van een meisje uit kinderdagverblijf B wordt dus als volgt berekend:

Aan de andere kant, om de waarschijnlijkheid te bepalen dat we een jongen selecteren op een kinderdagverblijf, moeten we eerst de waarschijnlijkheid vinden dat we een jongen selecteren voor elke kinderopvang en deze vervolgens bij elkaar optellen:

Voordelen van boomstructuur

Vanwege de kenmerken van de boomstructuur zijn de voordelen van dit type statistische grafiek als volgt:

• Boomdiagrammen zijn erg handig bij het nemen van beslissingen.
• De relatie tussen alle mogelijke uitkomsten kan grafisch worden weergegeven.
• Het is erg handig om de oorzaak van een probleem te vinden.
• Maakt het gemakkelijker om waarschijnlijkheids- en statistische problemen op te lossen.
• Een boomdiagram helpt bij het ordenen van ideeën en het analyseren van de situatie.