Hoe te bootstrapping in r (met voorbeelden)

Bootstrapping is een methode die kan worden gebruikt om de standaardfout van een statistiek te schatten en een betrouwbaarheidsinterval voor de statistiek te genereren.

Het basisproces voor bootstrapping is als volgt:

• Neem k replicaatmonsters met vervanging uit een gegeven dataset.
• Bereken voor elk monster de betreffende statistiek.
• Dit levert k verschillende schattingen op voor een bepaalde statistiek, die u vervolgens kunt gebruiken om de standaardfout van de statistiek te berekenen en een betrouwbaarheidsinterval voor de statistiek te creëren.

We kunnen in R opstarten met behulp van de volgende functies uit de bootstrapbibliotheek :

1. Genereer bootstrap-voorbeelden.

boot(gegevens, statistieken, R, …)

Goud:

• gegevens: een vector, matrix of blok gegevens
• statistiek: een functie die de te starten statistiek(en) produceert
• A: Aantal bootstrap-herhalingen

2. Genereer een bootstrap-betrouwbaarheidsinterval.

boot.ci(opstartobject, conf, type)

Goud:

• bootobject: een object dat wordt geretourneerd door de functie boot().
• conf: het betrouwbaarheidsinterval dat moet worden berekend. De standaardwaarde is 0,95
• type: Type betrouwbaarheidsinterval dat moet worden berekend. Opties omvatten ’standaard‘, ‚basic‘, ’stud‘, ‚perc‘, ‚bca‘ en ‚all‘ – standaard is ‚all‘

De volgende voorbeelden laten zien hoe u deze functies in de praktijk kunt gebruiken.

Voorbeeld 1: start een enkele statistiek

De volgende code laat zien hoe u de standaardfout voor het R-kwadraat van een eenvoudig lineair regressiemodel kunt berekenen:

 set.seed(0)
library (boot)

#define function to calculate R-squared
rsq_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
     original bias std. error
t1* 0.7183433 0.002164339 0.06513426

Uit de resultaten kunnen we zien:

• De geschatte R-kwadraat voor dit regressiemodel is 0,7183433 .
• De standaardfout voor deze schatting is 0,06513426 .

We kunnen ook snel de distributie van bootstrapped samples visualiseren:

 plot(reps)

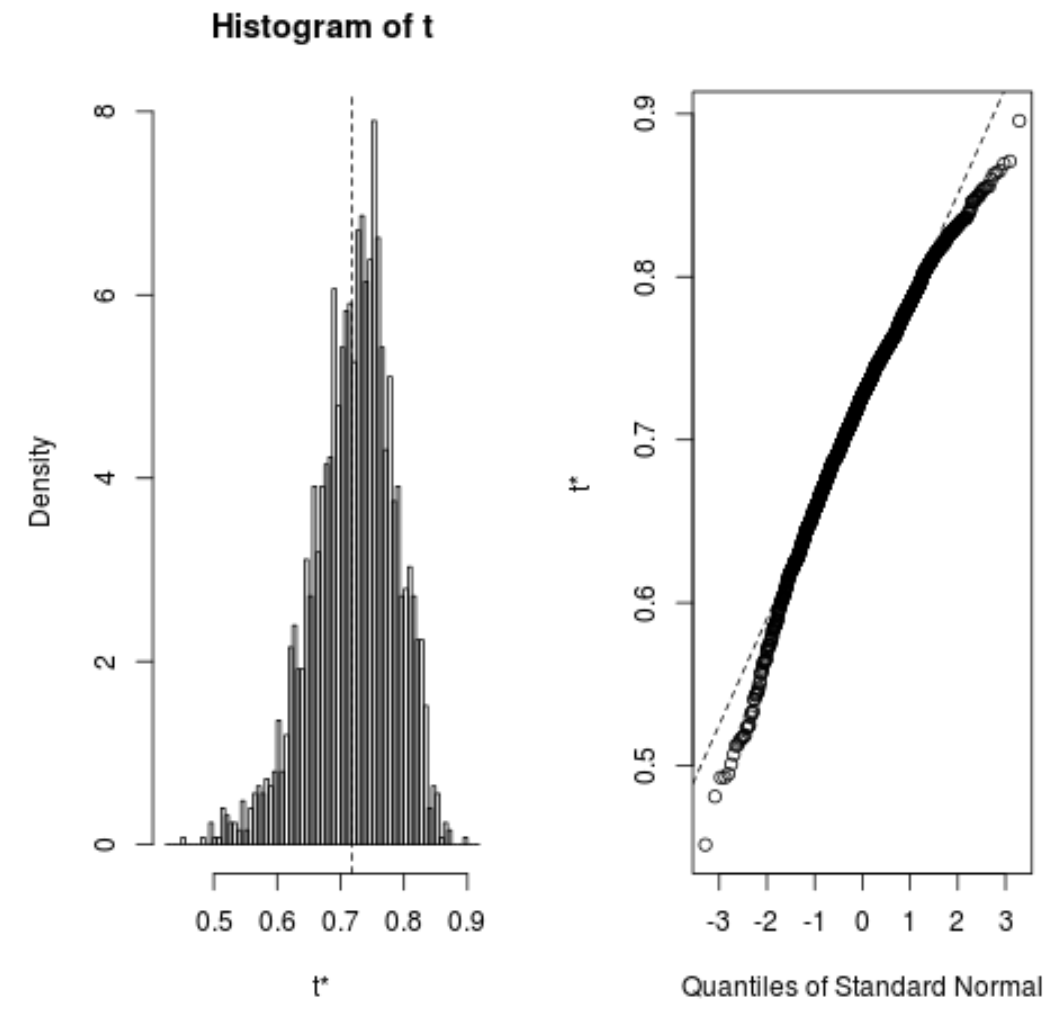
We kunnen ook de volgende code gebruiken om het 95% betrouwbaarheidsinterval voor het geschatte R-kwadraat van het model te berekenen:

 #calculate adjusted bootstrap percentile (BCa) interval
boot.ci(reps, type=" bca ")

CALL: 
boot.ci(boot.out = reps, type = "bca")

Intervals: 
Level BCa          
95% (0.5350, 0.8188)  
Calculations and Intervals on Original Scale

Uit het resultaat kunnen we zien dat het bootstrapped-betrouwbaarheidsinterval van 95% voor de echte R-kwadraatwaarden (0,5350, 0,8188) is.

Voorbeeld 2: meerdere statistieken opstarten

De volgende code laat zien hoe u de standaardfout voor elke coëfficiënt in een meervoudig lineair regressiemodel kunt berekenen:

 set.seed(0)
library (boot)

#define function to calculate fitted regression coefficients
coef_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (coef(fit)) #return coefficient estimates of model
}

#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
       original bias std. error
t1* 29.59985476 -5.058601e-02 1.49354577
t2* -0.04121512 6.549384e-05 0.00527082

Uit de resultaten kunnen we zien:

• De geschatte coëfficiënt voor het modelonderschepping is 29,59985476 en de standaardfout van deze schatting is 1,49354577 .
• De geschatte coëfficiënt voor de voorspellende variabele disp in het model is -0,04121512 en de standaardfout van deze schatting is 0,00527082 .

We kunnen ook snel de distributie van bootstrapped samples visualiseren:

 plot(reps, index=1) #intercept of model
plot(reps, index=2) #disp predictor variable

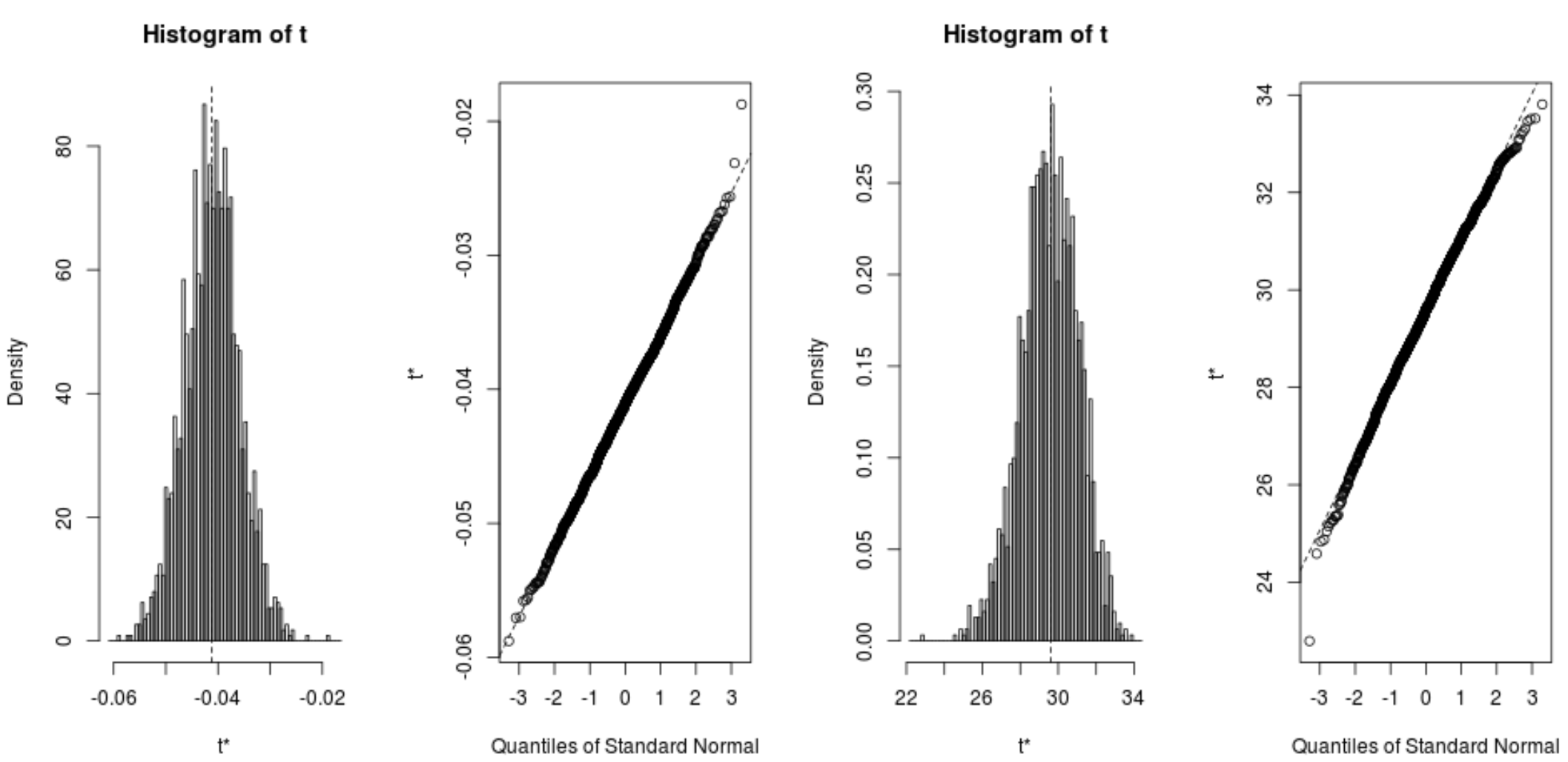
We kunnen ook de volgende code gebruiken om de 95%-betrouwbaarheidsintervallen voor elke coëfficiënt te berekenen:

 #calculate adjusted bootstrap percentile (BCa) intervals
boot.ci(reps, type=" bca ", index=1) #intercept of model
boot.ci(reps, type=" bca ", index=2) #disp predictor variable

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 1)

Intervals: 
Level BCa          
95% (26.78, 32.66)  
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 2)

Intervals: 
Level BCa          
95% (-0.0520, -0.0312)  
Calculations and Intervals on Original Scale

Uit de resultaten kunnen we zien dat de bootstrapped 95%-betrouwbaarheidsintervallen voor de modelcoëfficiënten als volgt zijn:

• IC voor onderschepping: (26.78, 32.66)
• CI voor weergave : (-.0520, -.0312)

Aanvullende bronnen

Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Inleiding tot betrouwbaarheidsintervallen