Boven- en onderhekken: definitie en voorbeeld

In statistieken vertegenwoordigen de boven- en ondergrenzen drempelwaarden voor de bovenste en onderste uitschieters in een dataset. Ze worden als volgt berekend:

• Lagere afsluiting = Q1 – (1,5*IQR)
• Bovenste sluiting = Q3 + (1,5*IQR)

waarbij IQR staat voor ‘interkwartielbereik’, wat het verschil vertegenwoordigt tussen het 75e percentiel (Q3) en het 25e percentiel (Q1) in een dataset.

Een waarneming die zich boven de bovenste barrière of onder de onderste barrière bevindt, wordt vaak als een uitbijter beschouwd.

Voorbeeld: Berekening van het bovenste en onderste hekwerk

Stel dat we de volgende dataset hebben:

 Dataset: 11, 13, 14, 14, 15, 16, 18, 22, 24, 27, 34, 36, 38, 41, 45

We kunnen de volgende stappen gebruiken om de bovenste en onderste omheining van de dataset te berekenen:

Stap 1: Zoek naar Q1 en Q3.

Q1 vertegenwoordigt het 25e percentiel van de dataset en Q3 vertegenwoordigt het 75e percentiel. Volgens de interkwartielbereikcalculator zijn Q1 en Q3 voor deze dataset:

• T1: 14
• T3: 36

Stap 2: Vind de IQR (interkwartielbereik).

De interkwartielafstand vertegenwoordigt het verschil tussen Q3 en Q1, dat als volgt wordt berekend:

• Interkwartielschaal: Q3 – Q1 = 36 – 14 = 22

Stap 3: Zoek het bovenste en onderste hek

We kunnen de volgende formules gebruiken om de bovenste en onderste hekken te berekenen:

• Lagere afsluiting: Q1 – (1,5*IQR) = 14 – (1,5*22) = -19
• Bovenhek: Q3 + (1,5*IQR) = 36 + (1,5*22) = 69

Omdat geen van de waarnemingen in onze dataset onder het onderste hek of boven het bovenste hek valt, zou geen van de waarnemingen als uitschieters worden beschouwd.

We kunnen ook een boxplot maken om onze verdeling van gegevenswaarden en de bovenste en onderste hekken te visualiseren:

Bonus: bovenste en onderste sluitcalculator

In plaats van handmatig de bovenste en onderste hekken van een dataset te berekenen, kunt u ook de bovenste en onderste hekkencalculator gebruiken:

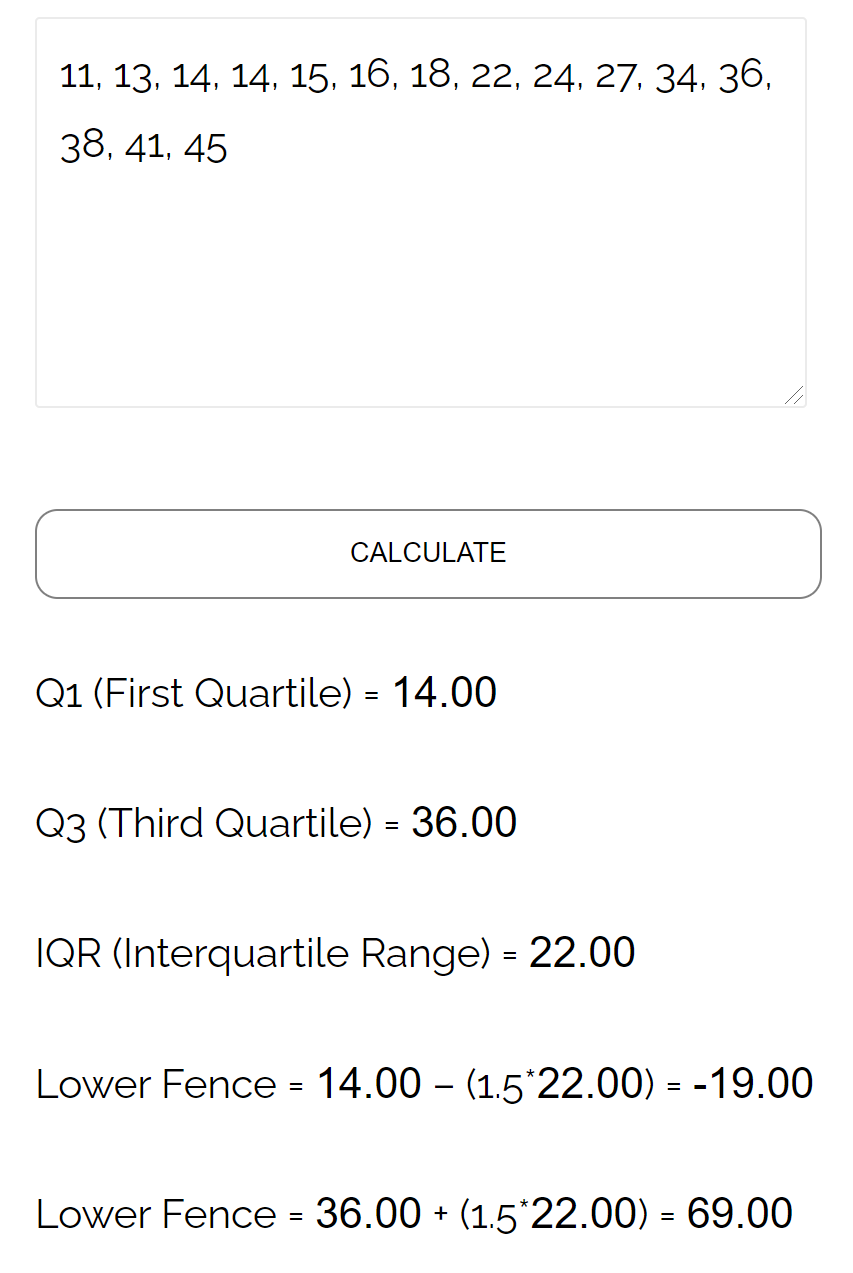
Op deze pagina vindt u nog meer handige statistische rekenmachines.