Een box-cox-transformatie uitvoeren in r (met voorbeelden)

Een box-cox-transformatie is een veelgebruikte methode voor het transformeren van een niet-normaal verdeelde dataset naar een meernormaal verdeelde set.

Het basisidee achter deze methode is om een waarde voor λ te vinden zodat de getransformeerde gegevens zo dicht mogelijk bij de normale verdeling liggen, met behulp van de volgende formule:

• y(λ) = (y ^λ – 1) / λ als y ≠ 0
• y(λ) = log(y) als y = 0

We kunnen een box-cox-transformatie in R uitvoeren met behulp van de boxcox()- functie uit de MASS()- bibliotheek. Het volgende voorbeeld laat zien hoe u deze functie in de praktijk kunt gebruiken.

Raadpleeg dit artikel van de Universiteit van Connecticut voor een mooie samenvatting van de ontwikkeling van de Box-Cox-transformatie.

Voorbeeld: Box-Cox-transformatie in R

De volgende code laat zien hoe u een lineair regressiemodel aan een gegevensset kunt aanpassen en vervolgens de functie boxcox() kunt gebruiken om een optimale lambda te vinden om de responsvariabele te transformeren en in een nieuw model te passen.

 library (MASS)

#create data
y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8)
x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8)

#fit linear regression model
model <- lm(y~x)

#find optimal lambda for Box-Cox transformation 
bc <- boxcox(y ~ x)
(lambda <- bc$x[which.max(bc$y)])

[1] -0.4242424

#fit new linear regression model using the Box-Cox transformation
new_model <- lm(((y^lambda-1)/lambda) ~ x)

De optimale lambda bleek -0,4242424 te zijn. Het nieuwe regressiemodel verving dus de oorspronkelijke responsvariabele y door de variabele y = (y ^-0,4242424 – 1) / -0,4242424.

De volgende code laat zien hoe u twee QQ-plots in R kunt maken om de verschillen in residuen tussen de twee regressiemodellen te visualiseren:

 #define plotting area
op <- par(pty = "s", mfrow = c(1, 2))

#QQ plot for original model
qqnorm(model$residuals)
qqline(model$residuals)

#QQ plot for Box-Cox transformed model
qqnorm(new_model$residuals)
qqline(new_model$residuals)

#display both QQ plots
by(op)

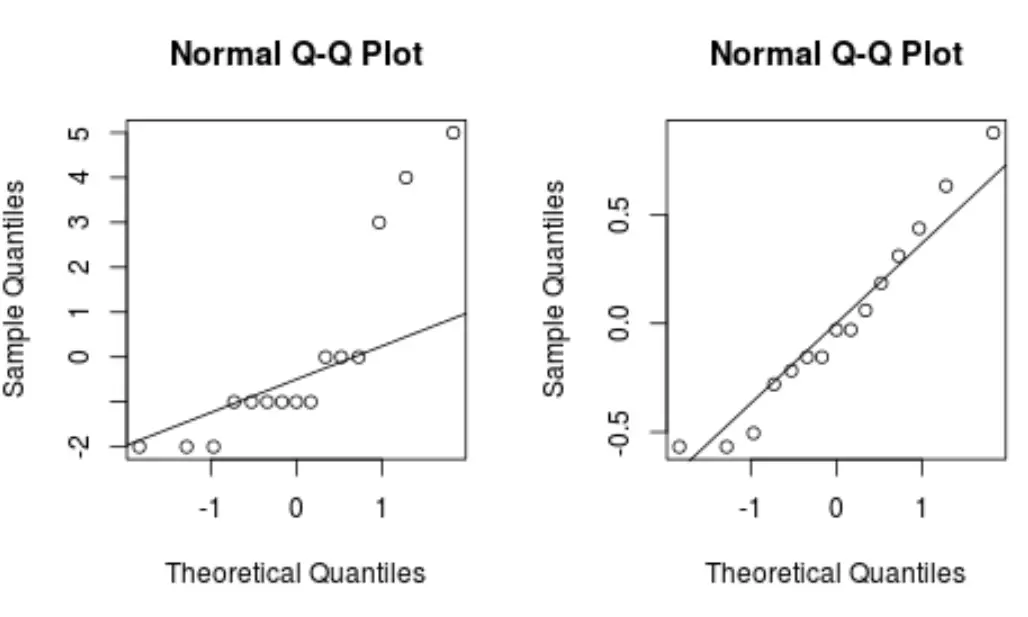
Als de datapunten in een QQ-plot langs een rechte diagonale lijn liggen, volgt de dataset over het algemeen waarschijnlijk een normale verdeling.

Merk op hoe het box-cox-getransformeerde model een QQ-plot produceert met een veel rechtere lijn dan het oorspronkelijke regressiemodel.

Dit geeft aan dat de residuen van het box-cox-getransformeerde model veel normaler verdeeld zijn, wat voldoet aan een van de aannames van lineaire regressie .

Aanvullende bronnen

Gegevens transformeren in R (logboek, vierkantswortel, kubuswortel)
Hoe u een QQ-plot in R maakt en interpreteert
Hoe een Shapiro-Wilk-test uit te voeren voor normaliteit in R