Hoe u een box-cox-transformatie uitvoert in python

Een box-cox-transformatie is een veelgebruikte methode voor het transformeren van een niet-normaal verdeelde dataset naar een meernormaal verdeelde set.

Het basisidee achter deze methode is om een waarde voor λ te vinden zodat de getransformeerde gegevens zo dicht mogelijk bij de normale verdeling liggen, met behulp van de volgende formule:

• y(λ) = (y ^λ – 1) / λ als y ≠ 0
• y(λ) = log(y) als y = 0

We kunnen een box-cox-transformatie uitvoeren in Python met behulp van de functie scipy.stats.boxcox() .

Het volgende voorbeeld laat zien hoe u deze functie in de praktijk kunt gebruiken.

Voorbeeld: Box-Cox-transformatie in Python

Stel dat we een willekeurige set van 1000 waarden genereren uit een exponentiële verdeling :

 #load necessary packages
import numpy as np 
from scipy. stats import boxcox 
import seaborn as sns 

#make this example reproducible
n.p. random . seeds (0)

#generate dataset
data = np. random . exponential (size= 1000 )

#plot the distribution of data values
sns. distplot (data, hist= False , kde= True ) 

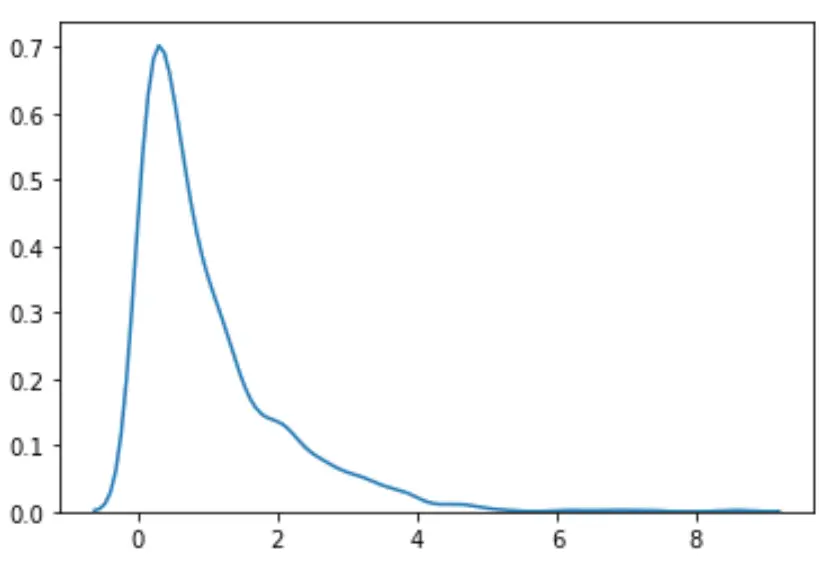
We kunnen zien dat de verdeling niet normaal lijkt.

We kunnen de functie boxcox() gebruiken om een optimale waarde van lambda te vinden die een meer normale verdeling oplevert:

 #perform Box-Cox transformation on original data
transformed_data, best_lambda = boxcox(data) 

#plot the distribution of the transformed data values
sns. distplot (transformed_data, hist= False , kde= True ) 

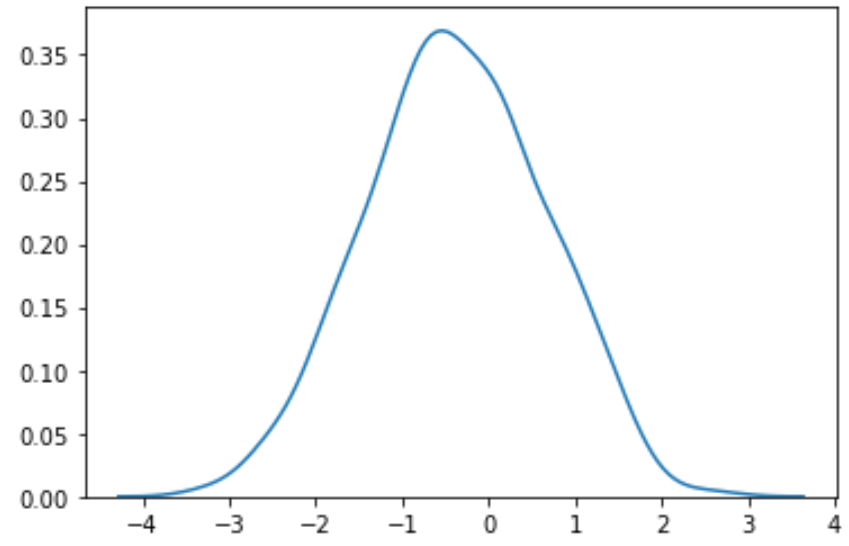
We kunnen zien dat de getransformeerde gegevens een veel normalere verdeling volgen.

We kunnen ook de exacte lambdawaarde vinden die is gebruikt om de Box-Cox-transformatie uit te voeren:

 #display optimal lambda value
print (best_lambda)

0.2420131978174143

De optimale lambda bleek rond de 0,242 te liggen.

Elke gegevenswaarde werd dus getransformeerd met behulp van de volgende vergelijking:

Nieuw = (oud ^0,242 – 1) / 0,242

We kunnen dit bevestigen door te kijken naar de waarden van de originele gegevens versus de getransformeerde gegevens:

 #view first five values of original dataset
data[0:5]

array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849])

#view first five values of transformed dataset
transformed_data[0:5]

array([-0.22212062, 0.23427768, -0.07911706, -0.23247555, -0.55495228])

De eerste waarde in de oorspronkelijke gegevensset was 0.79587 . Daarom hebben we de volgende formule toegepast om deze waarde te transformeren:

Nieuw = (.79587 ^0,242 – 1) / 0,242 = -0,222

We kunnen bevestigen dat de eerste waarde in de getransformeerde dataset inderdaad -0,222 is.

Aanvullende bronnen

Hoe u een QQ-plot in Python maakt en interpreteert
Hoe u een Shapiro-Wilk-normaliteitstest uitvoert in Python