Box- en snorhaarplot

In dit artikel wordt uitgelegd wat een boxplot, ook wel boxplot (of boxplot) genoemd, is. Je ontdekt hoe dit soort statistische diagrammen worden gemaakt en een opgeloste oefening van een box-and-whiskerdiagram en de interpretatie ervan.

Wat is een box-and-whisker-plot?

De boxplot , ook wel boxplot of boxplot genoemd, is een grafiek die visueel een reeks statistische gegevens weergeeft met behulp van kwartielen.

Het belangrijkste kenmerk van de box- enwhiskerplot is dat u hiermee snel de spreiding van een reeks gegevens kunt visualiseren, aangezien deze de kwartielen, de mediaan, de extreme waarden en de uitschieters van de gegevens aangeeft.

Dit type diagram bestaat dus uit een rechthoekige doos en een paar lijnen (of snorharen) waaruit de volgende waarden naar voren komen:

• De grenzen van het vak geven het eerste en derde kwartiel aan (Q ₁ en Q ₃ ). En de verticale lijn binnen de box is de mediaan (equivalent aan het tweede kwartiel _Q2 ).
• De grenzen van de snorharen (of armen) zijn de extreme waarden , dat wil zeggen de minimumwaarde en de maximumwaarde van de gegevensreeks.
• De punten buiten de snorharen zijn uitschieters , oftewel gegevens die waarschijnlijk verkeerd zijn gemeten en daarom niet in aanmerking mogen worden genomen in het statistische onderzoek.

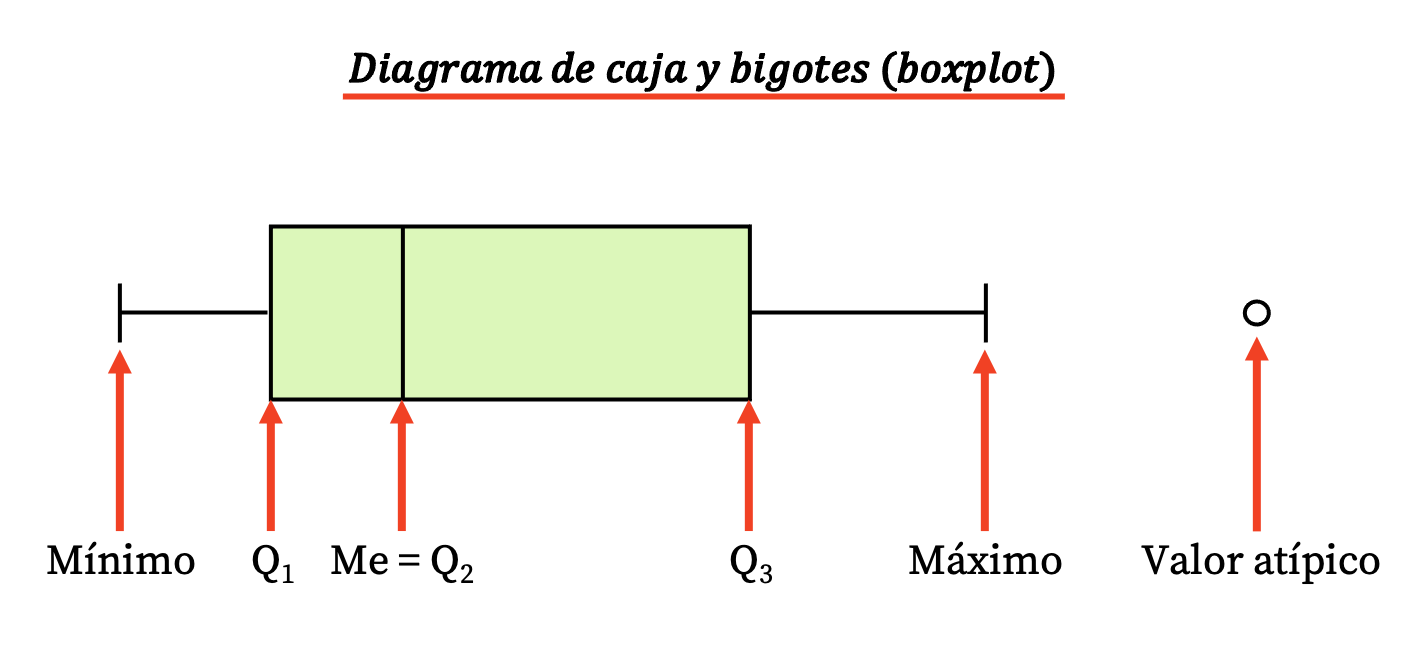
Merk op dat het verschil tussen het derde en het eerste kwartiel de interkwartielafstand (of interkwartielafstand) is, een andere maatstaf voor de statistische spreiding.

Box- enwhiskerplots zijn erg handig voor het vergelijken van numerieke variabelen. Het is echter niet geschikt voor het weergeven van categorische variabelen.

Hoe u een Box- en Whisker-plot maakt

Om een box-and-whiskerplot (of boxplot) te maken op basis van een gegevensreeks, moeten de volgende stappen worden uitgevoerd:

1. Sorteer de voorbeelden van statistische gegevens.
2. Bereken de kwartielen (Q ₁ , Q ₂ en Q ₃ ) en geef ze weer als het vak in het diagram. Het eerste en derde kwartiel komen overeen met de grenzen van het vak, en om de mediaan (het tweede kwartiel) weer te geven, moet je een lijn trekken binnen het vak waar de waarde zich bevindt.
3. Bereken het interkwartielbereik, dat gelijk is aan het derde kwartiel min het eerste kwartiel.



4. Bereken de toelaatbare waarden LI en LS, waarvan de formules zijn:





5. Identificeer steekproefuitschieters, dit zijn waarden kleiner dan LI of groter dan LS. Geef deze waarden buiten het snorhaarbereik weer met stippen.
6. Identificeer en representeer de extreme waarden, die de kleinste waarde en de grootste waarde zijn in het interval gevormd door LI en LS. Deze waarden vertegenwoordigen het einde van de twee snorharen in het diagram.

Box- en Whisker-plotvoorbeeld

Gezien de definitie en theorie van de box-and-whiskerplot (of boxplot), vindt u hieronder een concreet voorbeeld om het concept beter te begrijpen en te zien hoe dit type statistische plot wordt uitgevoerd.

• Teken een boxplot van de volgende statistische gegevensset.

In dit geval zijn de gegevens al geordend van klein naar groot, dus er zijn geen wijzigingen nodig. Anders moeten we eerst de voorbeeldgegevens sorteren.

Ten tweede extraheren we de kwartielen van de steekproef:

Nadat we de drie kwartielen hebben berekend, vinden we het interkwartielbereik door kwartiel 3 min kwartiel 1 af te trekken:

We berekenen nu de LI- en LS-limieten, dit zijn de waarden op basis waarvan gegevens als atypisch worden beschouwd. Om dit te doen, moet u de volgende formules gebruiken:

In dit geval hebben we dus twee uitschieters, omdat 3,02 kleiner is dan 3,16 en 5,71 groter is dan 5,56.

Ten slotte moeten nog de extreme waarden worden geïdentificeerd, die het minimum en het maximum zijn van alle gegevens die zich in het interval [LI,LS] bevinden. Daarom is in ons voorbeeld de minimumwaarde 3,70 en de maximumwaarde 4,81.

Dus zodra we alle waarden van de box en dewhiskerplot hebben geïdentificeerd, hoeft er alleen nog maar een grafische weergave te worden gemaakt:

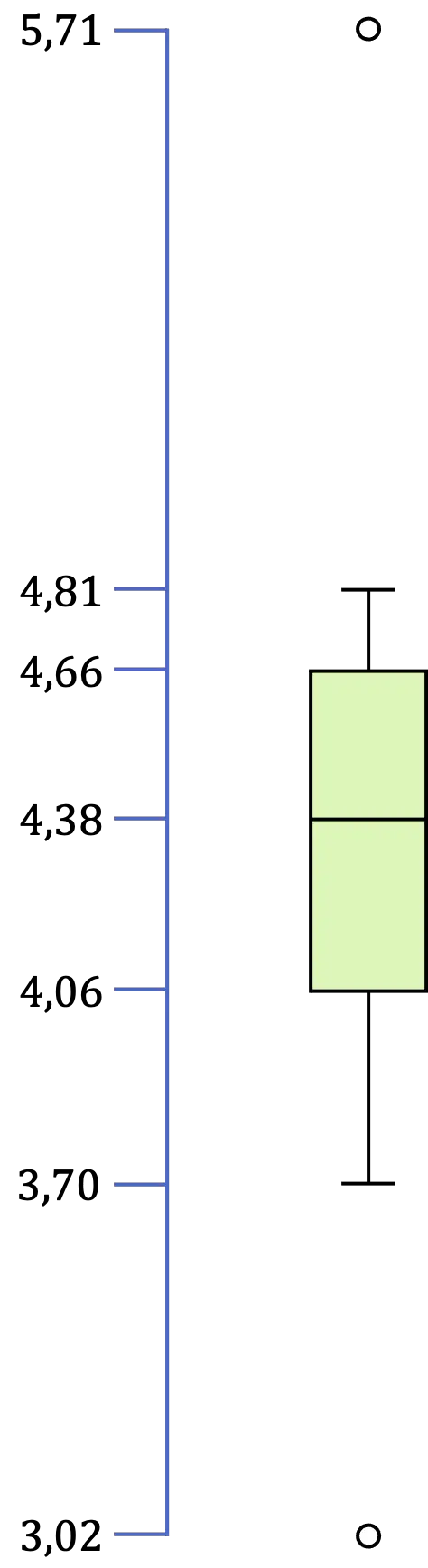
Waar wordt een box-and-whiskerplot voor gebruikt?

Laten we tot slot eens kijken waar het voor dient en hoe we de box-and-whisker-plot (of boxplot) moeten interpreteren.

Het is duidelijk dat de box-and-whiskerplot erg handig is om snel de kwartielen, het interkwartielbereik, de mediaan, extreme waarden en uitschieters van een gegevensreeks te kennen, aangezien al deze statistische metingen met een simpele blik kunnen worden geïdentificeerd.

Bovendien wordt de box-and-whiskerplot gebruikt om de symmetrie van de statistische steekproef te analyseren, aangezien deze visueel de volledige gegevensset vertegenwoordigt. Als de mediaan niet in het midden van de doos ligt, betekent dit dat het monster niet symmetrisch is.

Op dezelfde manier worden boxplots op de aandelenmarkt veel gebruikt om de variatie in de prijs van een aandeel over een bepaalde periode weer te geven, omdat ze het mogelijk maken om de maximale waarde, minimale waarde en tussenliggende waarden in een korte tijdsperiode te zien. tijd en dus sneller beslissingen nemen.