Een complete gids voor boxplotpercentages

Een boxplot is een type plot dat de vijfcijferige samenvatting van een dataset weergeeft, waaronder:

• De minimumwaarde
• Het eerste kwartiel
• De gemiddelde waarde
• Het derde kwartiel
• De maximale waarde

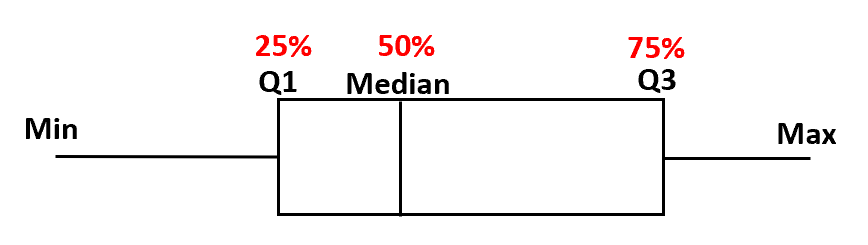
Een typische boxplot ziet er als volgt uit:

In een boxplot:

• Het eerste kwartiel vertegenwoordigt het 25e percentiel van alle waarden in de dataset.
• De mediaan vertegenwoordigt het 50e percentiel van alle waarden in de dataset.
• Het derde kwartiel vertegenwoordigt het 75e percentiel van alle waarden in de dataset.

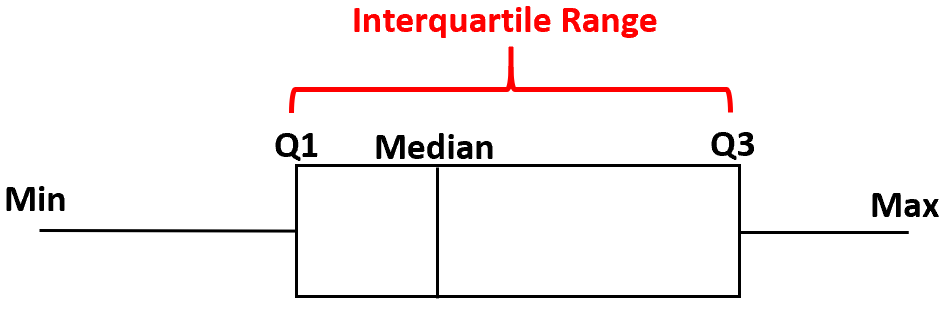
Het interkwartielbereik vertelt ons de verdeling van de middelste 50% van de waarden in een dataset en kan worden berekend door het eerste kwartiel af te trekken van het derde kwartiel in een boxplot:

In het volgende voorbeeld ziet u hoe u een boxplot kunt gebruiken om vragen over percentages te beantwoorden.

Voorbeeld: Boxplot-percentages interpreteren

De volgende boxplot toont de verdeling van eindexamenresultaten voor studenten in een bepaalde klas:

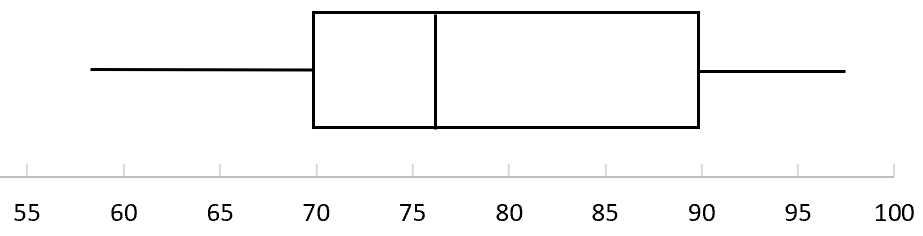
Gebruik de boxplot om de volgende vragen te beantwoorden.

Vraag 1: Welk percentage studenten scoorde onder de 70?

Uit de boxplot kunnen we zien dat 70 overeenkomt met het eerste kwartiel, dat het 25e percentiel vertegenwoordigt.

Zo behaalde 25% van de studenten een cijfer onder de 70.

Vraag 2: Welk percentage studenten scoorde boven de 90?

Uit de boxplot kunnen we zien dat 90 overeenkomt met het derde kwartiel, dat het 75e percentiel vertegenwoordigt.

Zo behaalde 25% van de studenten een cijfer boven de 90.

Vraag 3: Welk percentage studenten scoorde tussen de 70 en 90?

Uit de boxplot kunnen we zien dat 70 en 90 het eerste en derde kwartiel van de dataset vertegenwoordigen, die overeenkomen met het 25e en 75e percentiel.

Zo behaalde 75% – 25% = 50% van de studenten een score tussen 70 en 90.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over boxplots:

Boxplotgenerator
Boxplots vergelijken
Hoe asymmetrie in boxplots te identificeren