Boxplots vergelijken: met voorbeelden

Een boxplot is een type plot dat de vijfcijferige samenvatting van een dataset weergeeft, waaronder:

• De minimumwaarde
• Het eerste kwartiel (het 25e percentiel)
• De gemiddelde waarde
• Het derde kwartiel (het 75e percentiel)
• De maximale waarde

Om een boxplot te maken, tekenen we een box van het eerste tot en met het derde kwartiel. Vervolgens tekenen we een verticale lijn op de mediaan. Ten slotte tekenen we ‘snorharen’ van de kwartielen tot aan de minimale en maximale waarde.

Boxplots zijn nuttig omdat ze ons in staat stellen snel de verdeling van waarden in een dataset te begrijpen. Ze zijn ook nuttig voor het vergelijken van twee verschillende datasets.

Wanneer we twee of meer boxplots vergelijken, kunnen we vier verschillende vragen beantwoorden:

1. Hoe zijn de mediaanwaarden met elkaar te vergelijken? We kunnen de verticale lijn in elk vak vergelijken om te bepalen welke dataset een hogere mediaanwaarde heeft.

2. Hoe verhoudt de spreiding zich? We kunnen de lengte van elke box (die de afstand tussen Q1 en Q3 vertegenwoordigt – het interkwartielbereik) vergelijken om te bepalen welke dataset groter is.

3. Hoe verhoudt asymmetrie zich tot elkaar? Hoe dichter de verticale lijn bij het eerste kwartaal ligt, des te positiever is de dataset scheef. Hoe dichter de verticale lijn bij het derde kwartaal ligt, hoe schever de dataset.

4. Zijn er uitbijters aanwezig? In boxplots worden uitschieters meestal weergegeven door kleine cirkels die voorbij elke snorhaar reiken. Een waarneming wordt als uitbijter gedefinieerd als deze aan een van de volgende criteria voldoet:

• Eén waarneming is minder dan Q1 – 1,5*IQR
• Een waarneming is groter dan Q3 + 1,5*IQR

Het volgende voorbeeld laat zien hoe u twee verschillende boxplots kunt vergelijken en deze vier vragen kunt beantwoorden.

Voorbeeld: Boxplots vergelijken

De volgende datasets tonen de resultaten van studenten die een van de twee studietechnieken hebben gebruikt ter voorbereiding op het examen:

Methode 1: 78, 78, 79, 80, 80, 82, 82, 83, 83, 86, 86, 86, 86, 87, 87, 87, 88, 88, 88, 91

Methode 2: 66, 66, 66, 67, 68, 70, 72, 75, 75, 78, 82, 83, 86, 88, 89, 90, 93, 94, 95, 98

Als we voor elke dataset boxplots maken, zien ze er zo uit:

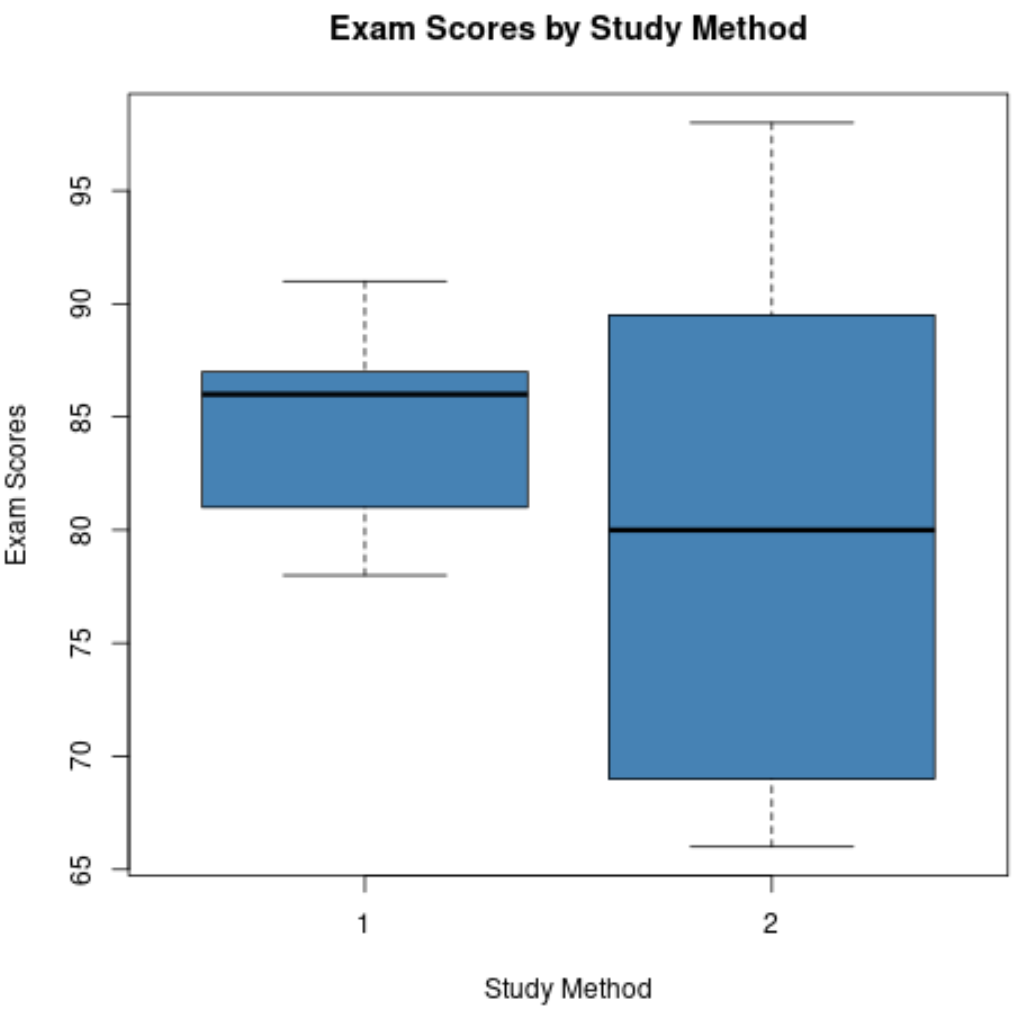
We kunnen deze twee boxplots vergelijken en de volgende vier vragen beantwoorden:

1. Hoe zijn de mediaanwaarden met elkaar te vergelijken? De lijn in het midden van de boxplot voor studiemethode 1 is hoger dan de lijn voor studiemethode 2, wat aangeeft dat studenten die studiemethode 1 gebruikten een gemiddeld cijfer behaalden op het hogere tentamen.

2. Hoe verhoudt de spreiding zich? De boxplot voor Studiemethode 2 is veel langer dan die voor Studiemethode 1, wat aangeeft dat examenscores veel meer verdeeld zijn onder studenten die Studiemethode 2 gebruikten.

3. Hoe verhoudt asymmetrie zich tot elkaar? De lijn in het midden van de boxplot voor studiemethode 1 ligt dicht bij Q3, wat aangeeft dat de verdeling van examenscores voor studenten die studiemethode 1 gebruikten negatief scheef is. Omgekeerd ligt de lijn in het midden van de boxplot bij studiemethode 2 dicht bij het midden van de box, wat betekent dat de verdeling van de scores minimaal scheef is.

4. Zijn er uitbijters aanwezig? Geen van beide boxplots heeft kleine cirkels die verder reiken dan de bovenste of onderste snorharen, wat betekent dat geen van beide datasets duidelijke uitschieters heeft.

Aanvullende bronnen

Boxplots maken en interpreteren in Excel
Boxplots maken en interpreteren in SPSS
Hoe u meerdere boxplots maakt in R
Boxplots maken en interpreteren in Stata