Bray-curtis-ongelijkheid: definitie en voorbeelden

Vernoemd naar J. Roger Bray en John Thomas Curtis , is de ongelijkheid tussen Bray en Curtis een manier om de ongelijkheid tussen twee verschillende locaties te meten.

Het wordt vaak gebruikt in de ecologie en biologie om het verschil tussen twee locaties te kwantificeren in termen van de soorten die op die locaties voorkomen.

De Bray-Curtis-ongelijkheid wordt als volgt berekend:

BC _ij = 1 – (2*C _ij ) / (S _ik + S _j )

Goud:

• C _ij : De som van de laagste waarden voor de soorten die op elke locatie voorkomen.
• S _i : Het totale aantal exemplaren geteld op locatie i
• S _j : Het totale aantal exemplaren geteld op locatie j

De Bray-Curtis-ongelijkheid ligt altijd tussen 0 en 1 waarbij:

• 0 geeft aan dat twee sites geen verschil vertonen. Met andere woorden, ze delen precies hetzelfde aantal van elk type soort.
• 1 geeft aan dat twee locaties volledig van elkaar verschillen. Met andere woorden, ze delen geen enkele soort van hetzelfde type.

Het volgende voorbeeld laat zien hoe u de Bray-Curtis-ongelijkheid voor twee locaties kunt berekenen.

Voorbeeld: berekening van de ongelijkheid tussen Bray en Curtis

Stel dat een botanicus eropuit gaat en het aantal van vijf verschillende plantensoorten (A, B, C, D en E) op twee verschillende locaties telt.

De volgende tabel vat de gegevens samen die ze heeft verzameld:

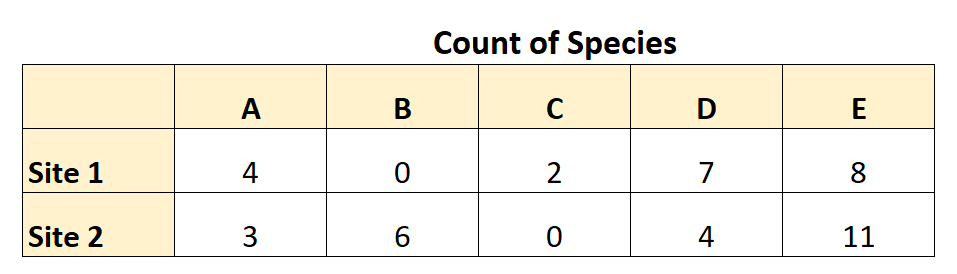
Met behulp van deze gegevens kan ze de Bray-Curtis-ongelijkheid als volgt berekenen:

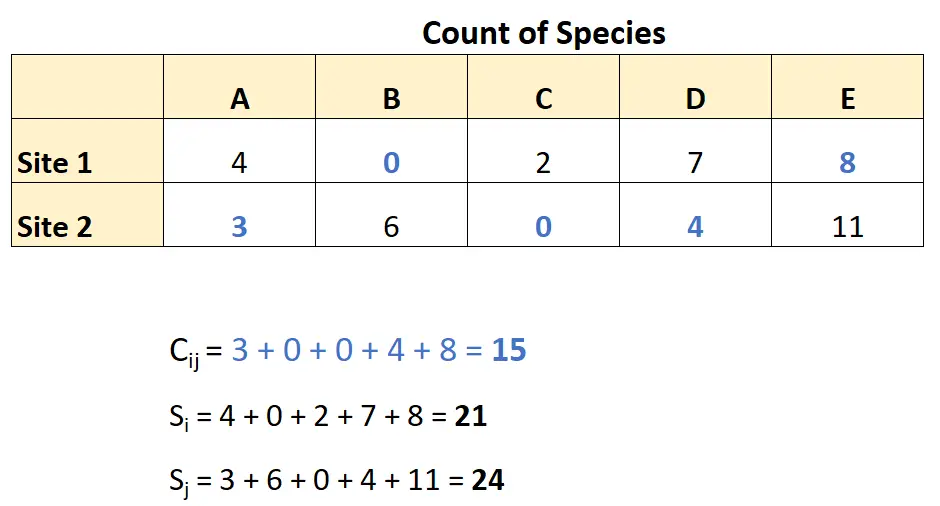
Door deze getallen te integreren in de Bray-Curtis-ongelijkheidsformule verkrijgen we:

• BC _ij = 1 – (2*C _ij ) / (S _ik + S _j )
• BC _ij = 1 – (2*15) / (21 + 24)
• _BCij = 0,33

Het Bray-Curtis-verschil tussen deze twee locaties bedraagt 0,33 .

Belangrijkste aanname van de ongelijkheid van Bray-Curtis

De ongelijkheid van Bray-Curtis gaat ervan uit dat de twee locaties even groot zijn.

Dit is een cruciale aanname, want als het ene gebied vier keer groter is dan het andere, zullen we uiteraard meer soorten in het grotere gebied hebben dan in het kleinere gebied, eenvoudigweg omdat er veel meer gebied te bestrijken is.

Om dit te illustreren, veronderstellen we dat een van de sites waarvoor de botanicus gegevens verzamelde vier keer groter is dan de andere site:

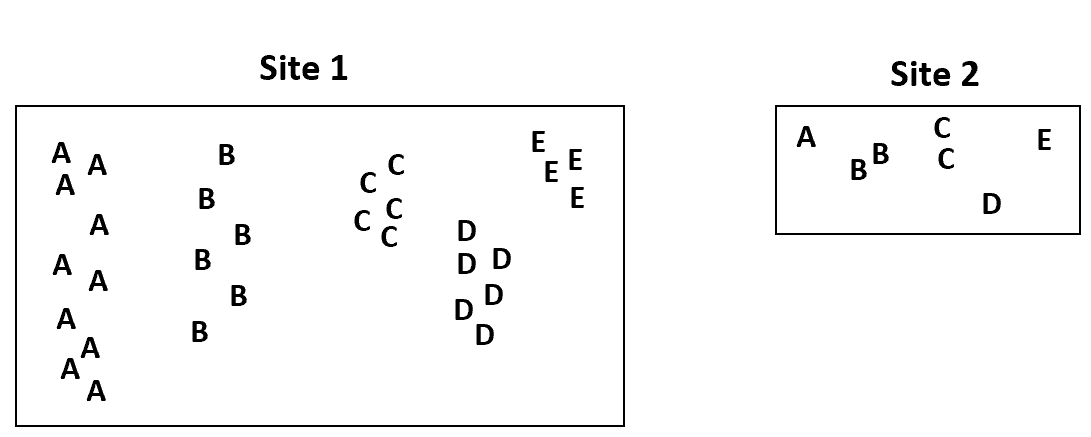
We zouden veel hogere frequenties van de soort op locatie 1 verwachten, simpelweg omdat deze veel groter is dan locatie 2.

Dus als we de Bray-Curtis-ongelijkheid berekenen, zou deze behoorlijk groot zijn. Dit zou echter misleidend zijn, omdat het verschil tussen de twee sites niet in de samenstelling zit, maar eerder in de omvang ervan.