Hoe de bray-curtis-ongelijkheid in r te berekenen

De ongelijkheid van Bray-Curtis is een manier om de ongelijkheid tussen twee verschillende locaties te meten.

Het wordt vaak gebruikt in de ecologie en biologie om het verschil tussen twee locaties te kwantificeren in termen van de soorten die op die locaties voorkomen.

Het wordt als volgt berekend:

BC _ij = 1 – (2*C _ij ) / (S _ik + S _j )

Goud:

• C _ij : De som van de laagste waarden voor de soorten die op elke locatie voorkomen.
• S _i : Het totale aantal exemplaren geteld op locatie i
• S _j : Het totale aantal exemplaren geteld op locatie j

De Bray-Curtis-ongelijkheid ligt altijd tussen 0 en 1 waarbij:

• 0 geeft aan dat twee sites geen verschil vertonen. Met andere woorden, ze delen precies hetzelfde aantal van elk type soort.
• 1 geeft aan dat twee locaties volledig van elkaar verschillen. Met andere woorden, ze delen geen enkele soort van hetzelfde type.

Stel bijvoorbeeld dat een botanicus op pad gaat en het aantal van vijf verschillende plantensoorten (A, B, C, D en E) op twee verschillende locaties telt.

De volgende tabel vat de gegevens samen die ze heeft verzameld:

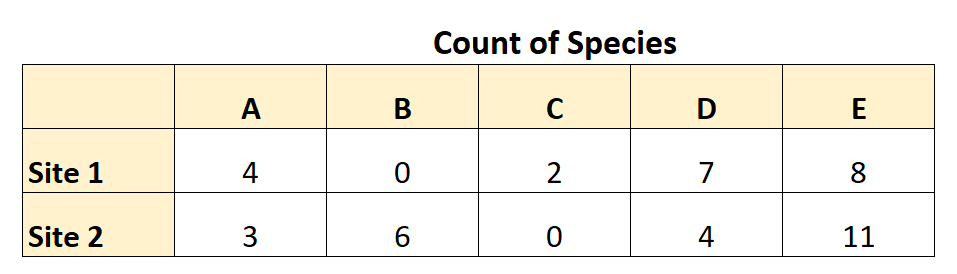
Met behulp van deze gegevens kan ze de Bray-Curtis-ongelijkheid als volgt berekenen:

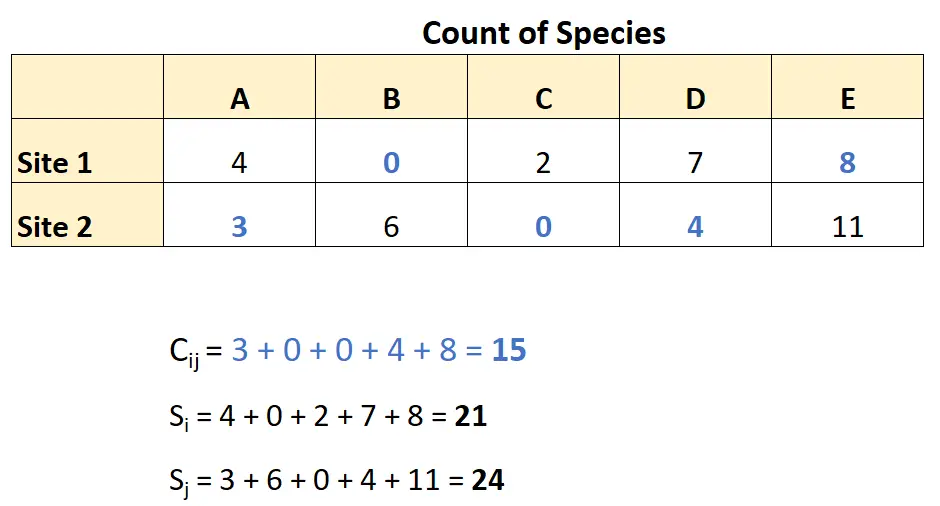
Door deze getallen te integreren in de Bray-Curtis-ongelijkheidsformule verkrijgen we:

• BC _ij = 1 – (2*C _ij ) / (S _ik + S _j )
• BC _ij = 1 – (2*15) / (21 + 24)
• _BCij = 0,33

Het Bray-Curtis-verschil tussen deze twee locaties bedraagt 0,33 .

Het volgende voorbeeld laat zien hoe u de Bray-Curtis-ongelijkheid in R kunt berekenen.

Voorbeeld: berekening van de Bray-Curtis-ongelijkheid in R

Laten we eerst het volgende dataframe in R maken om onze datawaarden vast te houden:

 #create data frame
df <- data. frame (A=c(4, 3),
                 B=c(0, 6),
                 C=c(2, 0),
                 D=c(7, 4),
                 E=c(8, 11))

#view data frame
df

  A B C D E
1 4 0 2 7 8
2 3 6 0 4 11

We kunnen de volgende code gebruiken om de Bray-Curtis-ongelijkheid tussen de twee rijen in het dataframe te berekenen:

 #calculate Bray–Curtis dissimilarity
sum( apply (df, 2, function (x) abs ( max (x)- min (x)))) / sum ( rowSums (df))

[1] 0.3333333

De Bray-Curtis blijkt anders 0,33 te zijn.

Dit komt overeen met de waarde die we eerder handmatig hebben berekend.

Opmerking : deze formule werkt alleen als elke rij in het gegevensframe een afzonderlijke site vertegenwoordigt.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere gelijkenisstatistieken in R kunt berekenen:

Hoe Jaccard-gelijkenis in R te berekenen
Hoe cosinusovereenkomst in R te berekenen