Hoe een breusch-pagan-test uit te voeren in stata

Meervoudige lineaire regressie is een methode die we kunnen gebruiken om de relatie tussen meerdere verklarende variabelen en een responsvariabele te begrijpen.

Helaas staat een probleem dat vaak voorkomt bij regressie bekend als heteroscedasticiteit , waarbij er een systematische verandering is in de variantie van de residuen over een reeks gemeten waarden.

Eén test die we kunnen gebruiken om te bepalen of heteroskedasticiteit aanwezig is, is de Breusch-Pagan-test . Deze test levert een Chi-kwadraat-teststatistiek en een overeenkomstige p-waarde op.

Als de p-waarde onder een bepaalde drempel ligt (veel voorkomende keuzes zijn 0,01, 0,05 en 0,10), dan is er voldoende bewijs om te zeggen dat er sprake is van heteroscedasticiteit.

In deze tutorial wordt uitgelegd hoe u een Breusch-Pagan-test uitvoert in Stata.

Voorbeeld: Breusch-Pagan-test in Stata

We zullen de automatisch geïntegreerde Stata-dataset gebruiken om te illustreren hoe de Breusch-Pagan-test moet worden uitgevoerd.

Stap 1: Gegevens laden en weergeven.

Gebruik eerst de volgende opdracht om de gegevens te laden:

automatisch gebruik van het systeem

Geef vervolgens de onbewerkte gegevens weer met behulp van de volgende opdracht:

br

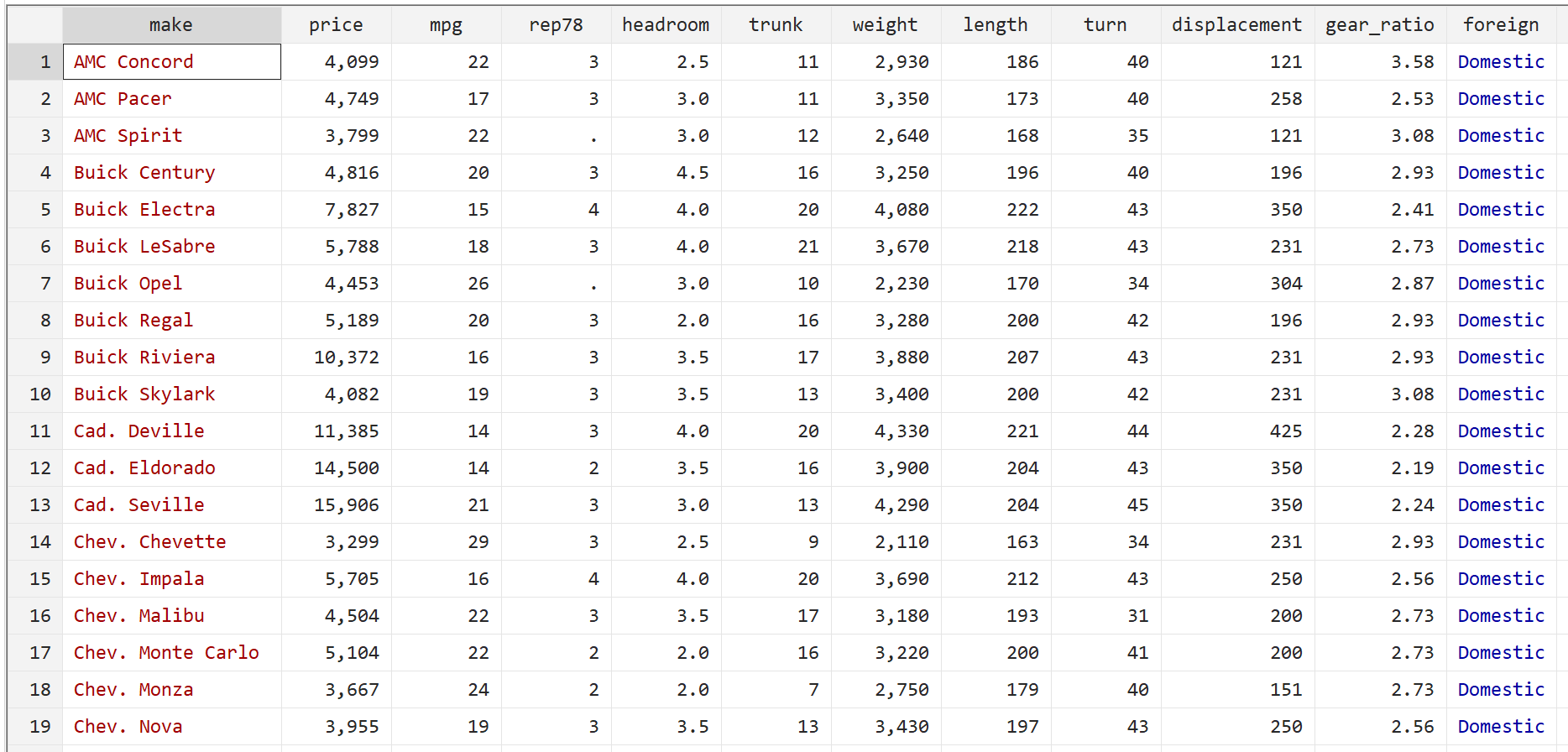
Stap 2: Voer meerdere lineaire regressie uit.

Vervolgens voeren we de volgende opdracht in om een meervoudige lineaire regressie uit te voeren, waarbij prijs als antwoordvariabele en mpg en gewicht als verklarende variabelen worden gebruikt:

regressie prijs mpg gewicht

Stap 3: Voer de Breusch-Pagan-test uit.

Zodra we het regressiemodel hebben aangepast, kunnen we de Breusch-Pagan-test uitvoeren met behulp van het hettest- commando, wat een afkorting is van „heteroscedasticiteitstest“:

de heetste

Zo interpreteert u het resultaat:

Ho: Dit is de nulhypothese van de test, die stelt dat er een constante variantie bestaat tussen de residuen.

Variabelen: Dit vertelt ons de responsvariabele die in het regressiemodel is gebruikt. In dit geval was het de variabele prijs .

chi2(1): Dit is de chikwadraattoetsstatistiek van de toets. In dit geval is het 14:78 uur.

Prob > chi2: Dit is de p-waarde die overeenkomt met de chikwadraattoetsstatistiek. In dit geval is dit 0,0001. Omdat deze waarde kleiner is dan 0,05, kunnen we de nulhypothese verwerpen en concluderen dat er heteroscedasticiteit in de gegevens zit.

Wat nu te doen

Als je er niet in slaagt de nulhypothese van de Breusch-Pagan-test te verwerpen, is er geen sprake van heteroscedasticiteit en kun je doorgaan met het interpreteren van het resultaat van de oorspronkelijke regressie.

Als u echter de nulhypothese van de Breusch-Pagan-test verwerpt, betekent dit dat er heteroscedasticiteit aanwezig is in de gegevens. In dit geval zijn de standaardfouten die worden weergegeven in de regressie-uitvoertabel onbetrouwbaar. Er zijn verschillende manieren om dit probleem op te lossen, waaronder:

1. Transformeer de responsvariabele. U kunt proberen een transformatie uit te voeren op de responsvariabele. U kunt bijvoorbeeld log(price) gebruiken in plaats van price als antwoordvariabele. Over het algemeen is het nemen van de log van de responsvariabele een effectieve manier om heteroscedasticiteit te elimineren. Een andere veel voorkomende transformatie is het gebruik van de vierkantswortel van de responsvariabele.

2. Gebruik gewogen regressie. Dit type regressie kent een gewicht toe aan elk gegevenspunt op basis van de variantie van de aangepaste waarde. In wezen geeft dit een laag gewicht aan datapunten met grotere varianties, waardoor hun resterende kwadraten kleiner worden. Wanneer de juiste gewichten worden gebruikt, kan dit het probleem van heteroskedasticiteit elimineren.

3. Gebruik robuuste standaardfouten. Robuuste standaardfouten zijn „robuuster“ voor het probleem van heteroskedasticiteit en bieden doorgaans een nauwkeuriger maatstaf voor de werkelijke standaardfout van een regressiecoëfficiënt. Bekijk deze tutorial om te leren hoe u robuuste standaardfouten kunt gebruiken bij regressie in Stata.