Brown-forsythe-test in r: stapsgewijs voorbeeld

Een one-way ANOVA wordt gebruikt om te bepalen of er al dan niet een significant verschil is tussen de gemiddelden van drie of meer onafhankelijke groepen.

Een van de aannames van een eenrichtings-ANOVA is dat de varianties van de populaties waaruit de steekproeven worden getrokken gelijk zijn.

Een van de meest gebruikelijke manieren om dit te testen is het gebruik van een Brown-Forsythe-test , een statistische test die gebruik maakt van de volgende aannames :

• H ₀ : De varianties tussen populaties zijn gelijk.
• H _A : De verschillen tussen populaties zijn niet gelijk.

Als de p-waarde van de test onder een bepaald significantieniveau ligt (bijvoorbeeld α = 0,05), dan verwerpen we de nulhypothese en concluderen we dat de varianties niet gelijk zijn tussen verschillende populaties.

Deze zelfstudie biedt een stapsgewijs voorbeeld van hoe u een Brown-Forsythe-test uitvoert in R.

Stap 1: Voer de gegevens in

Stel dat we willen weten of drie verschillende trainingsprogramma’s al dan niet tot verschillende niveaus van gewichtsverlies leiden.

Om dit te testen, rekruteren we 90 mensen en wijzen we willekeurig 30 mensen toe om elk programma te gebruiken. Vervolgens meten we het gewichtsverlies van elke persoon na één maand.

De volgende gegevensset bevat informatie over de hoeveelheid gewicht die u met elk programma verliest:

 #make this example reproducible
set.seed(0)

#create data frame
data <- data.frame(program = as . factor ( rep (c(" A ", " B ", " C "), each = 30)),
                   weight_loss = c( runif (30, 0, 3),
                                   runif (30, 0, 5),
                                   runif (30, 1, 7)))

#view first six rows of data frame
head(data)

# program weight_loss
#1 A 2.6900916
#2 A 0.7965260
#3 A 1.1163717
#4 A 1.7185601
#5 A 2.7246234
#6 A 0.6050458

Stap 2: Vat de gegevens samen en visualiseer ze

Voordat we een Brown-Forsythe-test uitvoeren, kunnen we boxplots maken om de variantie in gewichtsverlies voor elke groep te visualiseren:

 boxplot(weight_loss ~ program, data = data)

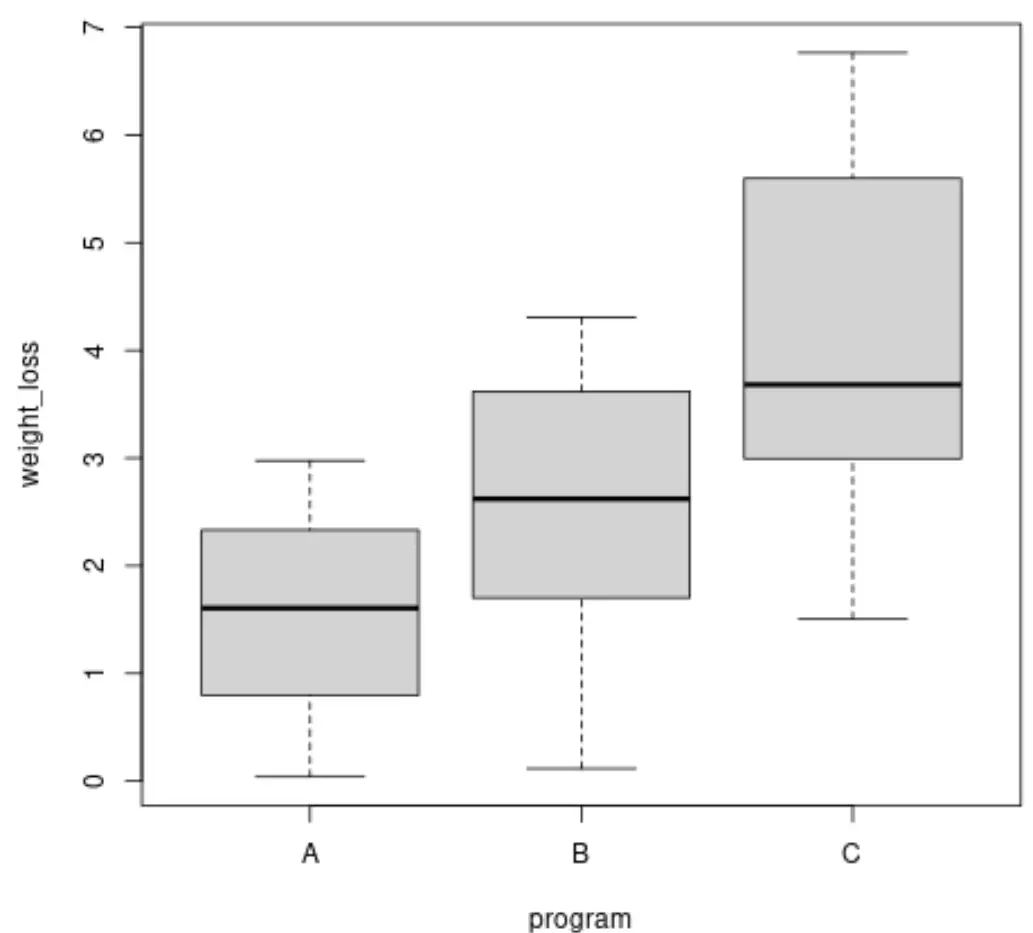
We kunnen ook de variantie van het gewichtsverlies in elke groep berekenen:

 #load dplyr package
library (dplyr)

#calculate variance of weight loss by group
data %>%
group_by (program) %>%
  summarize (var=var(weight_loss))

# A tibble: 3 x 2
  program var
     
1 A 0.819
2 B 1.53 
3 C 2.46

We kunnen zien dat de varianties tussen groepen verschillen, maar om te bepalen of deze verschillen statistisch significant zijn, kunnen we de Brown-Forsythe-test uitvoeren.

Stap 3: Voer de Brown-Forsythe-test uit

Om een Brown-Forsythe-test in R uit te voeren, kunnen we de functie bf.test() uit het onewaytests- pakket gebruiken:

 #load onewaytests package
library (onewaytests)

#perform Brown-Forsythe test
bf.test(weight_loss ~ program, data = data)

  Brown-Forsythe Test (alpha = 0.05) 
-------------------------------------------------- ----------- 
  data: weight_loss and program 

  statistic: 30.83304 
  num df: 2 
  name df: 74.0272 
  p.value: 1.816529e-10 

  Result: Difference is statistically significant. 
-------------------------------------------------- -----------

De p-waarde van de test blijkt kleiner dan 0,000 en, zoals het resultaat aangeeft, zijn de verschillen in varianties tussen de drie groepen statistisch significant.

Volgende stappen

Als u de nulhypothese van de Brown-Forsythe-test niet kunt verwerpen, kunt u een eenrichtings-ANOVA op de gegevens uitvoeren.

Als u echter de nulhypothese verwerpt, betekent dit dat de aanname van gelijkheid van varianties wordt geschonden. In dit geval heeft u twee opties:

1. Voer toch een one-way ANOVA uit.

Het blijkt dat een eenrichtings-ANOVA feitelijk robuust is tegen ongelijke varianties, zolang de grootste variantie niet groter is dan vier keer de kleinste variantie.

In stap 2 van het bovenstaande voorbeeld hebben we vastgesteld dat de kleinste variantie 0,819 was en de grootste variantie 2,46. De verhouding tussen de grootste en de kleinste variantie is dus 2,46 / 0,819 = 3,003 .

Omdat deze waarde kleiner is dan 4, kunnen we eenvoudigweg de eenrichtings-ANOVA uitvoeren.

2. Voer een Kruskal-Wallis-test uit

Als de verhouding tussen de grootste variantie en de kleinste variantie groter is dan 4, kan men ervoor kiezen om in plaats daarvan een Kruskal-Wallis-test uit te voeren. Dit wordt beschouwd als het niet-parametrische equivalent van eenrichtings-ANOVA.

Een stapsgewijs voorbeeld van een Kruskal-Wallis-test in R vindt u hier .