Wat is een categorische verdeling?

Een categorische verdeling is een discrete kansverdeling die de waarschijnlijkheid beschrijft dat een willekeurige variabele een waarde aanneemt die tot een van de K- categorieën behoort, waarbij elke categorie aan een waarschijnlijkheid is gekoppeld.

Om een uitkering als een categorische uitkering te kunnen classificeren, moet deze aan de volgende criteria voldoen:

• De categorieën zijn discreet.
• Er zijn twee of meer potentiële categorieën.
• De kans dat de willekeurige variabele in elke categorie een waarde aanneemt, moet tussen 0 en 1 liggen.
• De som van de kansen voor alle categorieën moet opgeteld 1 zijn.

Het meest voor de hand liggende voorbeeld van een categorische verdeling is de verdeling van de uitkomsten die gepaard gaan met het gooien van een dobbelsteen. Er zijn K = 6 mogelijke uitkomsten en de waarschijnlijkheid van elke uitkomst is 1/6:

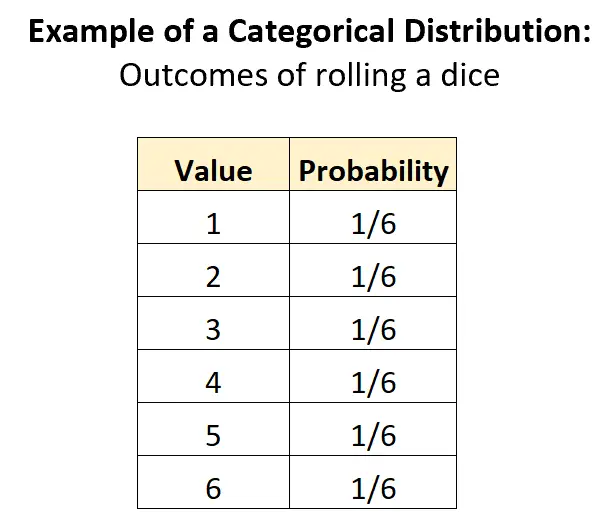
Deze verdeling voldoet aan alle criteria om als categorische verdeling te worden aangemerkt:

• De categorieën zijn discreet (de willekeurige variabele kan bijvoorbeeld alleen discrete waarden aannemen – 1, 2, 3, 4, 5, 6)
• Er zijn twee of meer potentiële categorieën.
• De waarschijnlijkheid van elke categorie ligt tussen 0 en 1.
• De som van de kansen is in totaal 1: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

Algemene regel:

Als je het aantal uitkomsten kunt tellen , dan werk je met een discrete willekeurige variabele, bijvoorbeeld door het aantal keren te tellen dat een munt kop oplevert.

Maar als je de uitkomst kunt meten , werk je met een continue willekeurige variabele, bijvoorbeeld het meten van lengte, gewicht, tijd, enz.

Andere voorbeelden van categorische verdelingen

Er zijn veel categorische distributies in de echte wereld, waaronder:

Voorbeeld 1: Draai een munt op.

Wanneer we een munt opgooien, zijn er twee potentiële afzonderlijke uitkomsten, de waarschijnlijkheid van elke uitkomst ligt tussen 0 en 1, en de som van de kansen is gelijk aan 1:

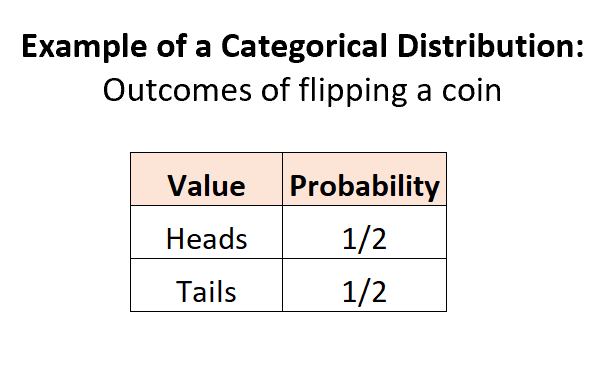
Voorbeeld 2: Selectie van knikkers in een urn.

Stel dat er in een urn 5 rode knikkers, 3 groene knikkers en 2 paarse knikkers zitten. Als we willekeurig een bal uit de urn selecteren, zijn er 3 potentiële afzonderlijke uitkomsten, de waarschijnlijkheid van elke uitkomst ligt tussen 0 en 1, en de som van de kansen is gelijk aan 1:

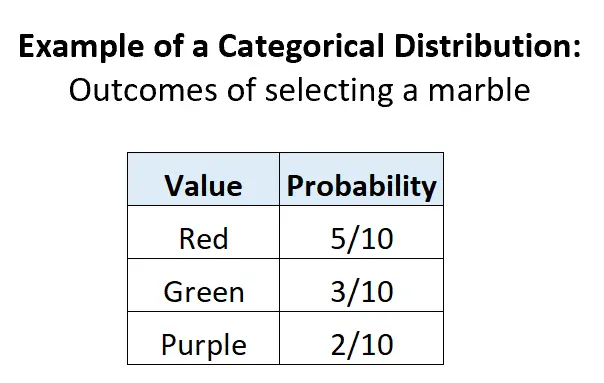
Voorbeeld 3: Een kaart uit een kaartspel selecteren.

Als we willekeurig een kaart selecteren uit een standaard kaartspel van 52 kaarten, zijn er 13 potentiële afzonderlijke uitkomsten, de waarschijnlijkheid van elke uitkomst ligt tussen 0 en 1, en de som van de kansen is gelijk aan 1:

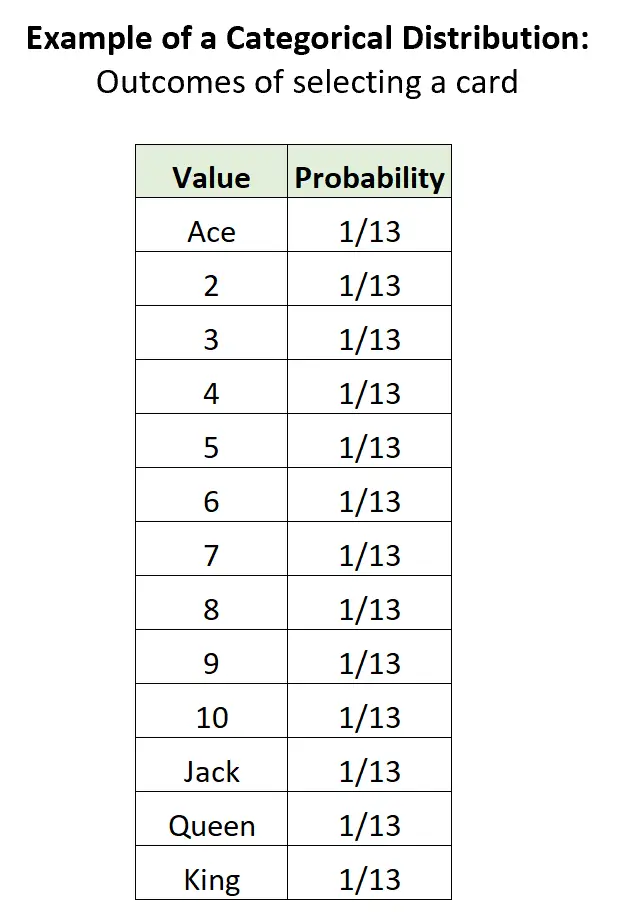
Relatie met andere distributies

Om een verdeling als een categorische verdeling te kunnen classificeren, moet deze K ≥ 2 potentiële uitkomsten hebben en n = 1 onderzoek.

Met behulp van deze terminologie is een categorische verdeling vergelijkbaar met de volgende verdelingen:

Bernoulli-verdeling: K = 2 resultaten, n = 1 test

Binominale verdeling: K = 2 eindpunten, n ≥ 1 proef

Multinomiale verdeling: K ≥ 2 resultaten, n ≥ proef

Aanvullende bronnen

Wat zijn willekeurige variabelen?
Een inleiding tot de binominale verdeling
Een inleiding tot multinomiale distributie