Normale cdf gebruiken in r (met voorbeelden)

U kunt de volgende methoden gebruiken om met de normale CDF (cumulatieve verdelingsfunctie) in R te werken:

Methode 1: Bereken normale CDF-kansen

 #calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)

#calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower.tail = FALSE )

Methode 2: Teken de normale CDF

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=" l ")

De volgende voorbeelden laten zien hoe u deze methoden in de praktijk kunt gebruiken.

Voorbeeld 1: Bereken normale CDF- kansen

De volgende code laat zien hoe je de kans berekent dat een willekeurige variabele een waarde kleiner dan 1,96 aanneemt in een standaard normale verdeling:

 #calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)

[1] 0.9750021

De kans dat een willekeurige variabele een waarde kleiner dan 1,96 aanneemt in een standaard normale verdeling is 0,975 .

We kunnen ook de waarschijnlijkheid bepalen dat een willekeurige variabele een waarde groter dan 1,96 aanneemt met behulp van het lower.tail- argument:

 #calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower.tail = FALSE )

[1] 0.0249979

En we kunnen de volgende syntaxis gebruiken om de waarschijnlijkheid te vinden dat een willekeurige variabele een waarde aanneemt tussen twee waarden in een standaard normale verdeling:

 #calculate probability that random value takes on value between -1.96 and 1.96
pnorm(1.96) - pnorm(-1.96)

[1] 0.9500042

De kans dat een willekeurige variabele een waarde aanneemt tussen -1,96 en 1,96 in een standaard normale verdeling is 0,95 .

Voorbeeld 2: De normale CDF plotten

De volgende code laat zien hoe u een normale CDF plot:

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=" l ") 

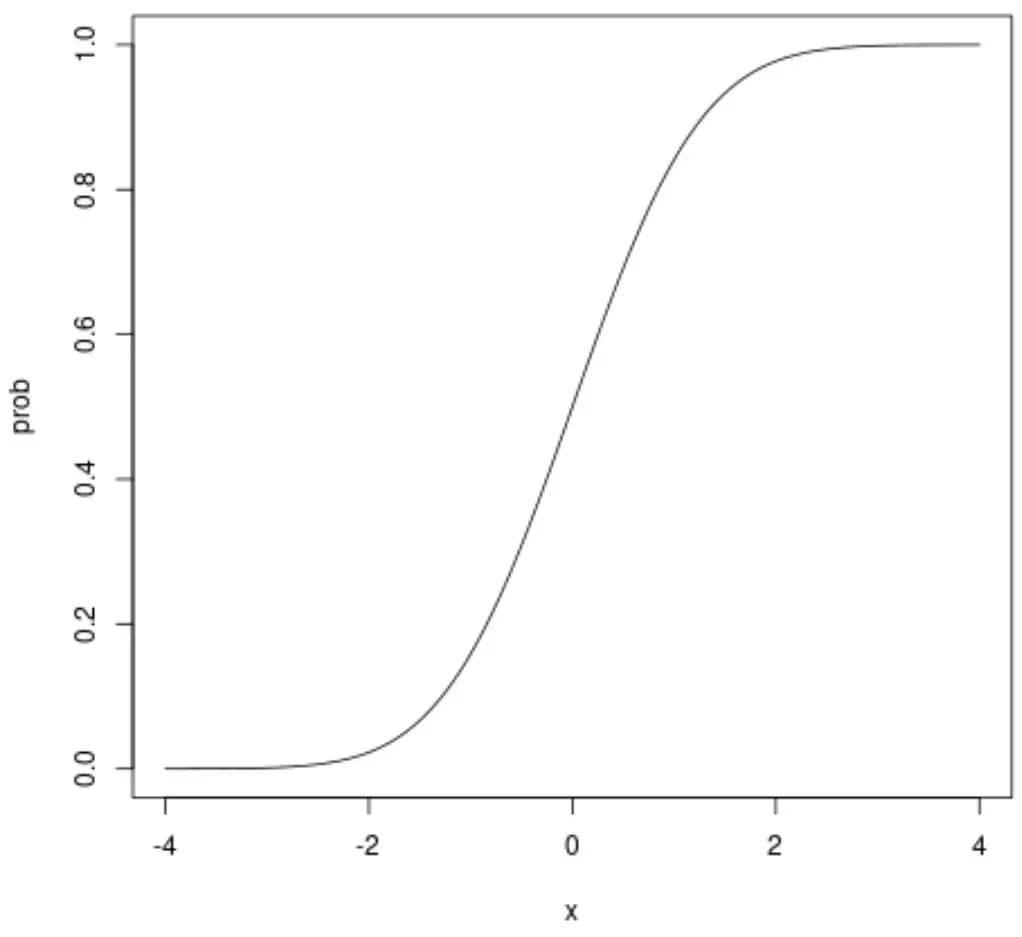
De x-as toont de waarden van een willekeurige variabele die een standaard normale verdeling volgt en de y-as toont de waarschijnlijkheid dat een willekeurige variabele een waarde aanneemt die kleiner is dan de waarde die op de x-as wordt weergegeven.

Als we bijvoorbeeld kijken naar x = 1,96, zien we dat de cumulatieve waarschijnlijkheid dat x kleiner is dan 1,96 ongeveer 0,975 is:

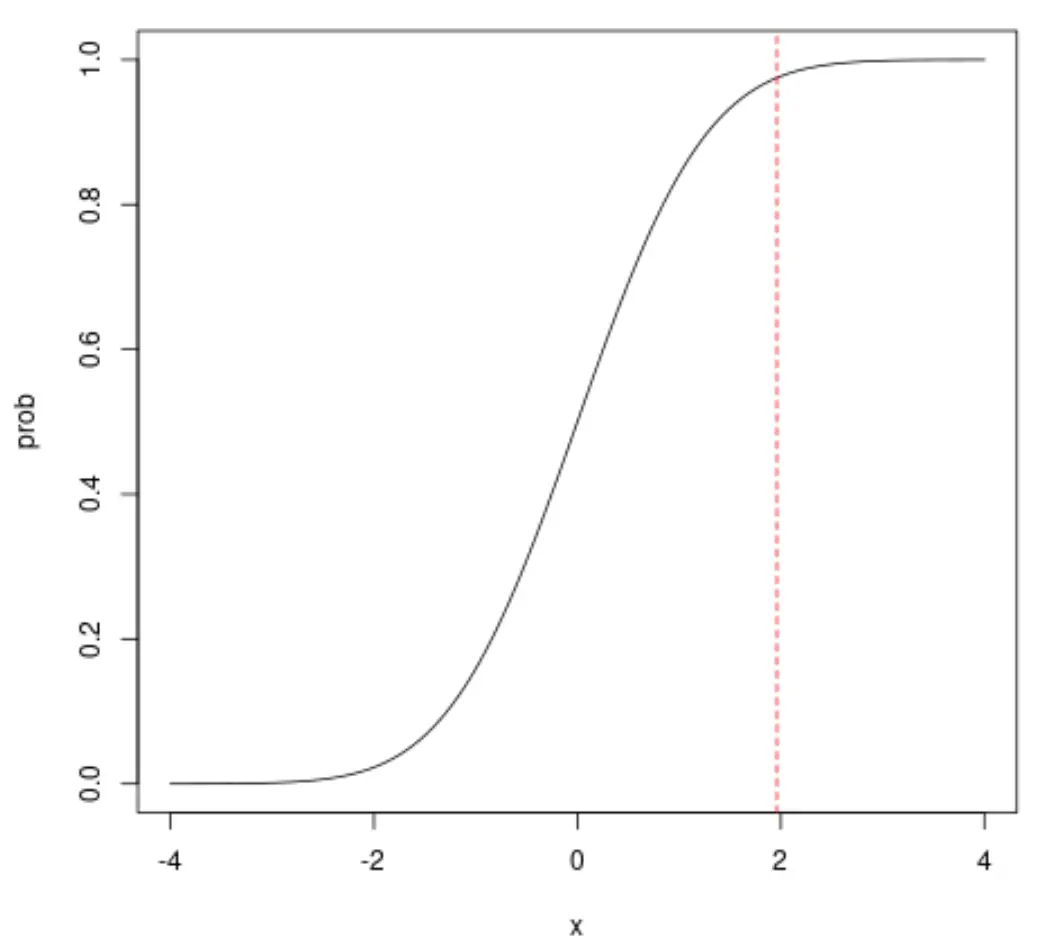
Merk op dat u ook de esthetiek van de normale CDF-plot kunt wijzigen:

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=' l ', col=' blue ', lwd= 2 , main=' Normal CDF ', ylab=' Cumulative Prob ') 

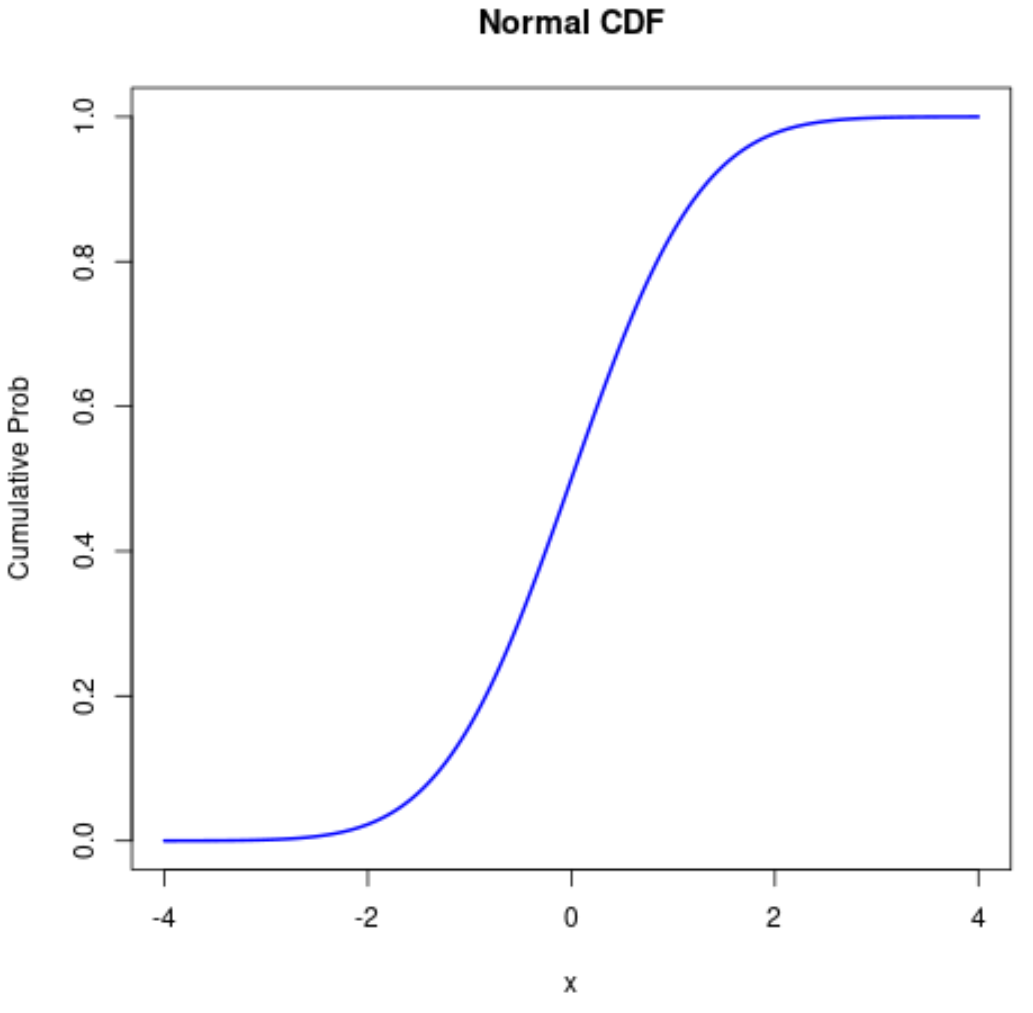
Gerelateerd: Hoe de seq-functie in R te gebruiken

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende bewerkingen in R kunt uitvoeren:

Hoe een normale verdeling in R te plotten
Hoe Z-scores in R te berekenen
Een gids voor dnorm, pnorm, qnorm en rnorm in R