Hoe de centrale limietstelling in excel toe te passen

De centrale limietstelling stelt dat de steekproefverdeling van een steekproefgemiddelde bij benadering normaal is als de steekproefomvang groot genoeg is, zelfs als de populatieverdeling niet normaal is .

De centrale limietstelling stelt ook dat de steekproefverdeling de volgende eigenschappen zal hebben:

1. Het gemiddelde van de steekproefverdeling zal gelijk zijn aan het gemiddelde van de populatieverdeling:

x = µ

2. De standaardafwijking van de steekproefverdeling is gelijk aan de standaardafwijking van de populatie gedeeld door de steekproefomvang:

s = σ / √n

In deze tutorial leggen we uit hoe je de centrale limietstelling in Excel kunt toepassen op een bepaalde verdeling.

De centrale limietstelling toepassen in Excel

Stel dat we een verdeling hebben met een gemiddelde van 8 en een standaarddeviatie van 4 . We kunnen de volgende formules in Excel gebruiken om zowel het gemiddelde als de standaardafwijking van de steekproefverdeling te vinden met een steekproefomvang van 15 :

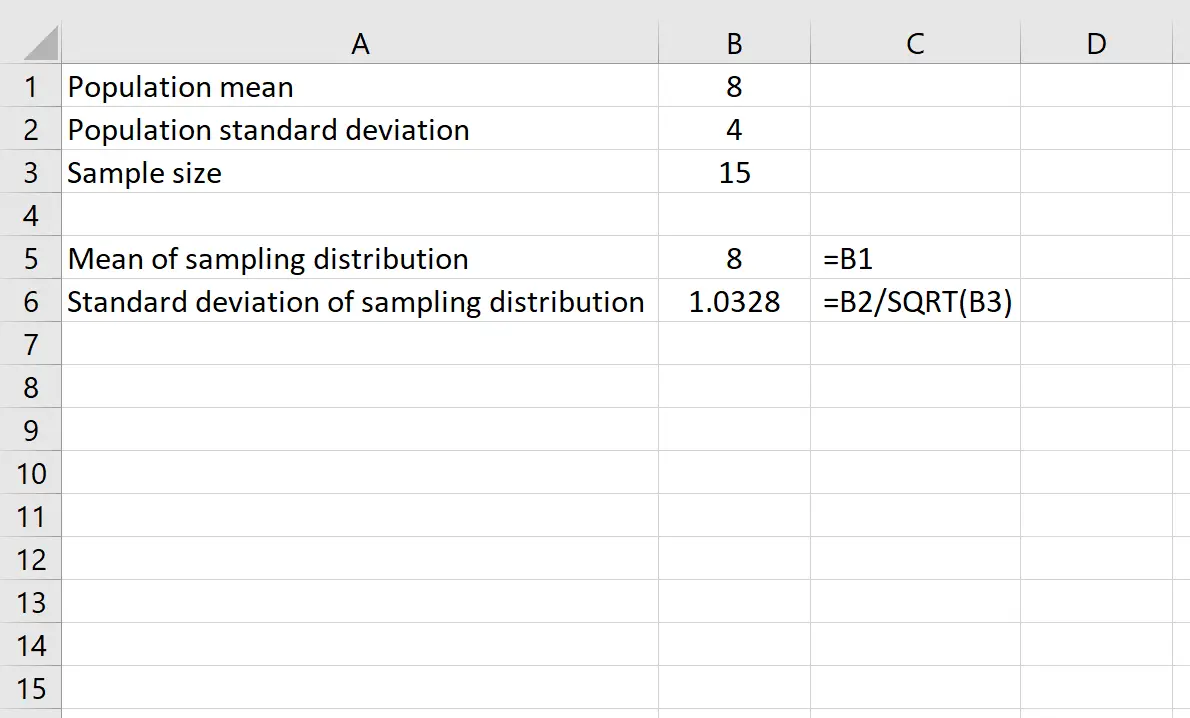
Het gemiddelde van de steekproefverdeling is eenvoudigweg gelijk aan het gemiddelde van de populatieverdeling, namelijk 8 .

De standaarddeviatie van de steekproefverdeling is gelijk aan de standaarddeviatie van de populatie gedeeld door de steekproefomvang, oftewel: 4 /√15 = 1,0328 .

We kunnen de centrale limietstelling ook gebruiken om vragen over waarschijnlijkheid te beantwoorden. Als een gegeven populatie bijvoorbeeld een gemiddelde van 8 en een standaarddeviatie van 4 heeft, wat is dan de kans dat een bepaalde steekproef van omvang 15   heeft een gemiddelde kleiner dan of gelijk aan 7 ?

Om deze vraag te beantwoorden, kunnen we de functie NORM.DIST() in Excel gebruiken, die de volgende syntaxis gebruikt:

NORM.VERD(x, gemiddelde, standaarddev, cumulatief)

Goud:

• x: monster betekent dat u wilt testen
• gemiddelde: verwachte gemiddelde van de steekproefverdeling
• standard_dev: verwachte standaardafwijking van de steekproefverdeling
• cumulatief: TRUE retourneert de normale CDF-waarde; FALSE retourneert de waarde van normale PDF. In ons geval gebruiken we altijd TRUE.

Deze functie retourneert de waarschijnlijkheid dat het steekproefgemiddelde kleiner is dan of gelijk is aan een bepaalde waarde.

Hier is de formule die we in dit voorbeeld zouden gebruiken:

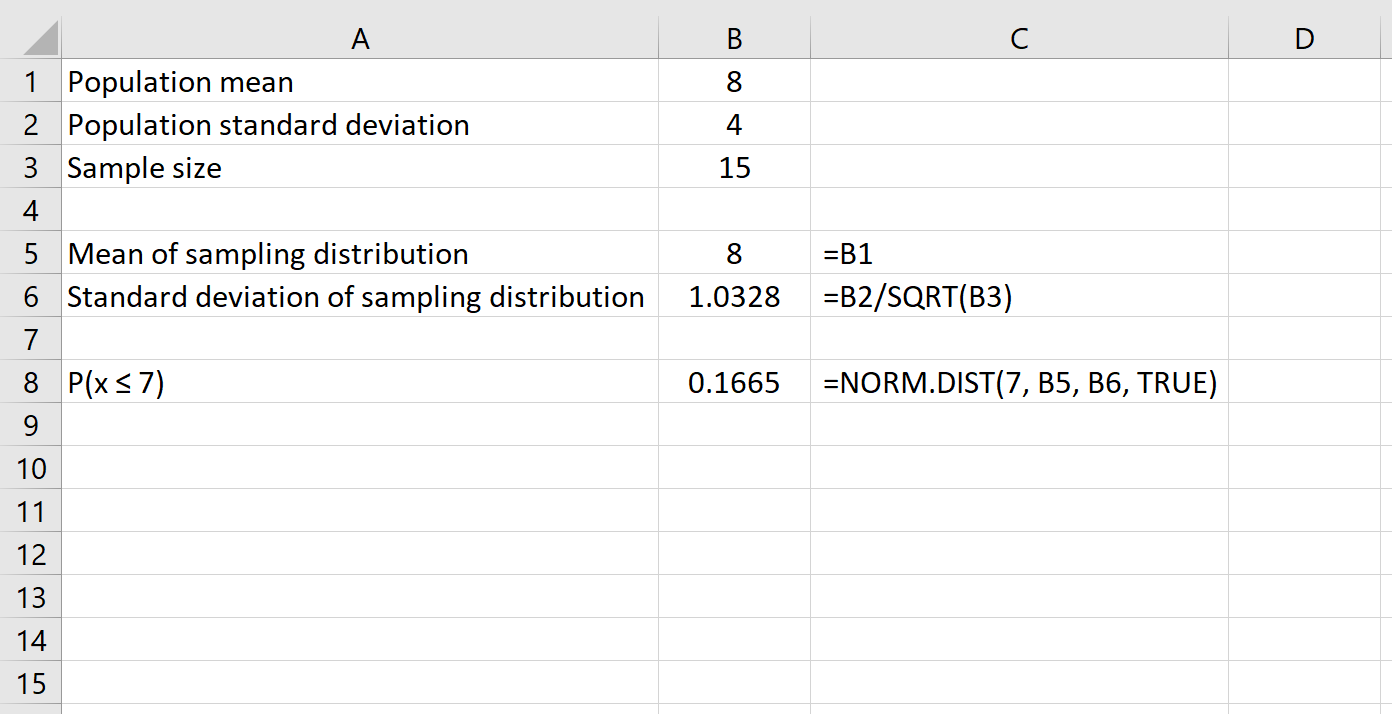
Dit vertelt ons dat voor een populatie met een gemiddelde van 8 en een standaarddeviatie van 4 de kans groot is dat een gegeven steekproef van grootte 15   heeft een gemiddelde kleiner dan of gelijk aan 7 of 0,1665 .

We kunnen ook de waarschijnlijkheid bepalen dat een bepaalde steekproefomvang een gemiddelde heeft dat groter is dan een bepaald getal door simpelweg formule 1 – NORM.DIST() te gebruiken.

De volgende formule laat bijvoorbeeld zien hoe je de waarschijnlijkheid kunt bepalen dat een gegeven steekproefomvang van 15 een gemiddelde groter dan 7 zal hebben:

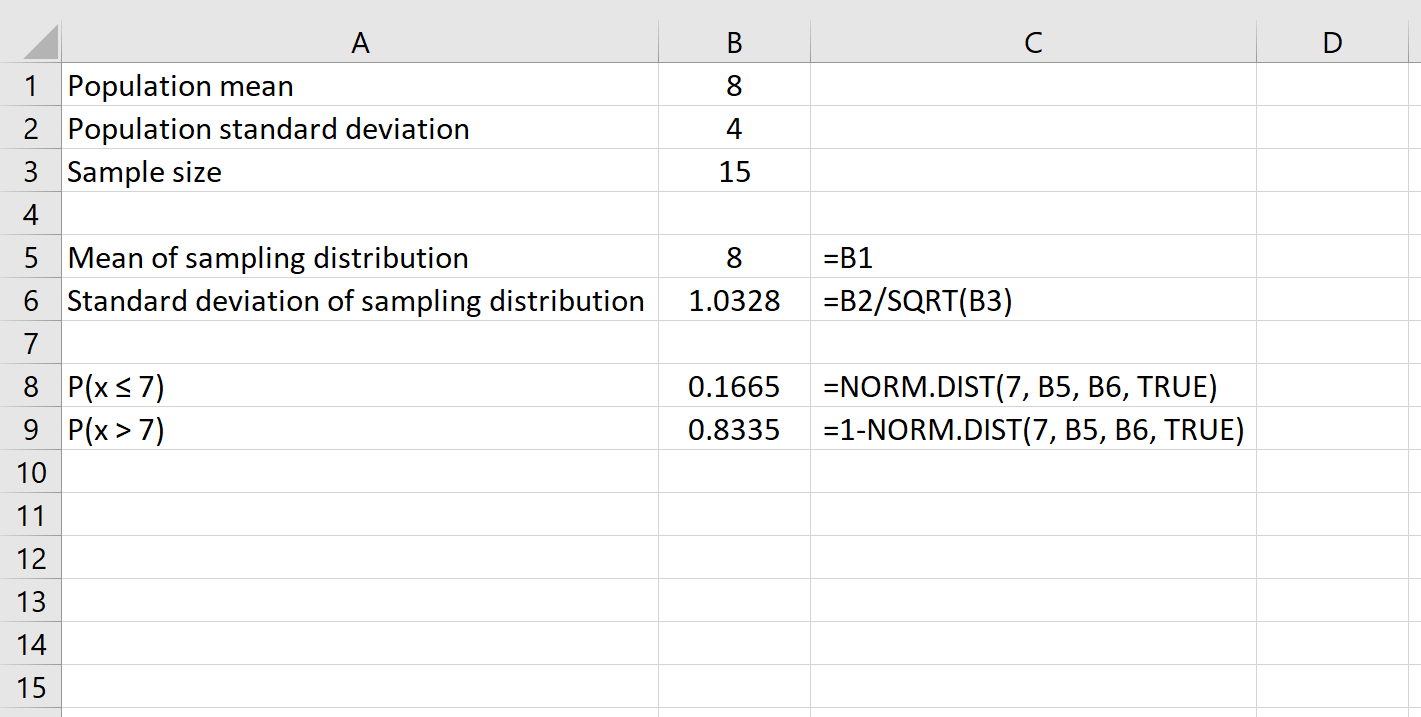
Ten slotte kunnen we de waarschijnlijkheid vinden dat een bepaalde steekproefomvang een gemiddelde tussen twee getallen heeft met behulp van de formule NORM.DIST(groter getal) – NORM.DIST(kleiner getal) .

De volgende formule laat bijvoorbeeld zien hoe je de waarschijnlijkheid kunt vinden dat een bepaalde steekproefomvang van 15 een gemiddelde tussen 7 en 9 heeft:

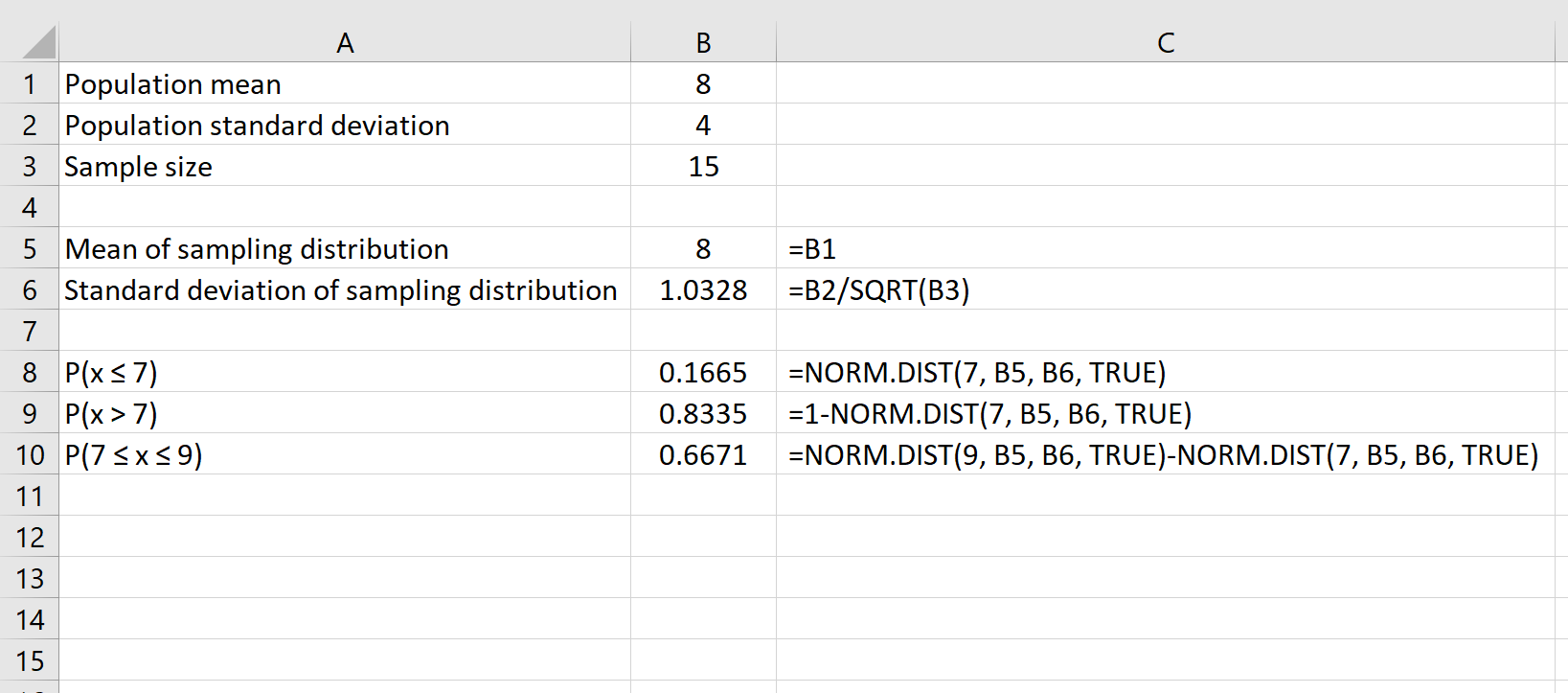
Aanvullende bronnen

Centrale limietstelling rekenmachine
Hoe u de vuistregel toepast in Excel
Hoe u een belcurve maakt in Excel