Hoe de centrale limietstelling in r toe te passen (met voorbeelden)

De centrale limietstelling stelt dat de steekproefverdeling van een steekproefgemiddelde bij benadering normaal is als de steekproefomvang groot genoeg is, zelfs als de populatieverdeling niet normaal is.

De centrale limietstelling stelt ook dat de steekproefverdeling de volgende eigenschappen zal hebben:

1. Het gemiddelde van de steekproefverdeling zal gelijk zijn aan het gemiddelde van de populatieverdeling:

x = µ

2. De standaardafwijking van de steekproefverdeling is gelijk aan de standaardafwijking van de populatieverdeling gedeeld door de steekproefomvang:

s = σ /n

Het volgende voorbeeld laat zien hoe u de centrale limietstelling in R kunt toepassen.

Voorbeeld: toepassing van de centrale limietstelling in R

Stel dat de breedte van het schild van een schildpad een uniforme verdeling volgt met een minimale breedte van 2 inch en een maximale breedte van 6 inch.

Dat wil zeggen, als we willekeurig een schildpad selecteren en de breedte van zijn schild meten, is deze waarschijnlijk ook tussen de 5 en 15 centimeter breed .

De volgende code laat zien hoe u een gegevensset in R kunt maken met de afmetingen van de schaalbreedte van 1.000 schildpadden, gelijkmatig verdeeld tussen 2 en 6 inch:

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

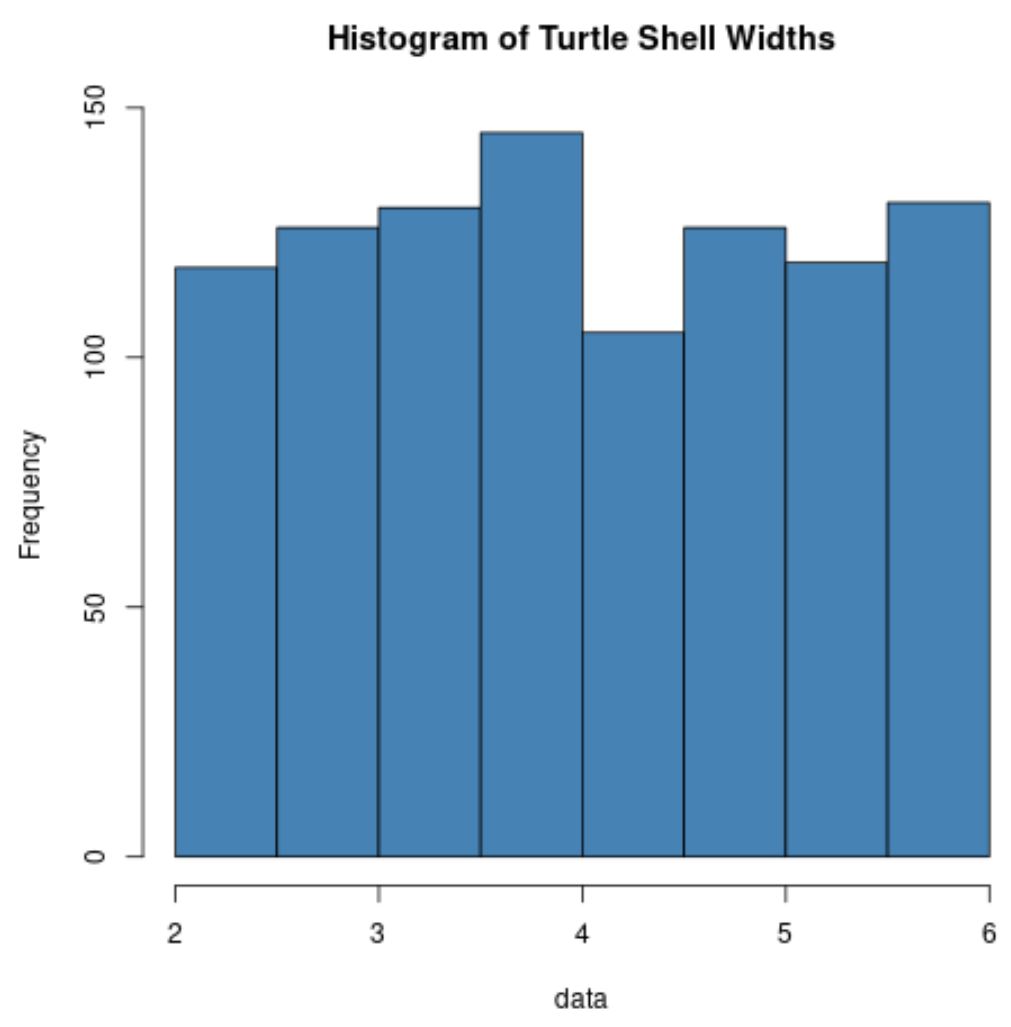
Merk op dat de verdeling van de breedte van schildpadden normaal gesproken helemaal niet verdeeld is.

Stel je nu voor dat we herhaalde willekeurige steekproeven nemen van vijf schildpadden uit deze populatie en het steekproefgemiddelde steeds opnieuw meten.

De volgende code laat zien hoe u dit proces in R uitvoert en een histogram maakt om de verdeling van steekproefgemiddelden te visualiseren:

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

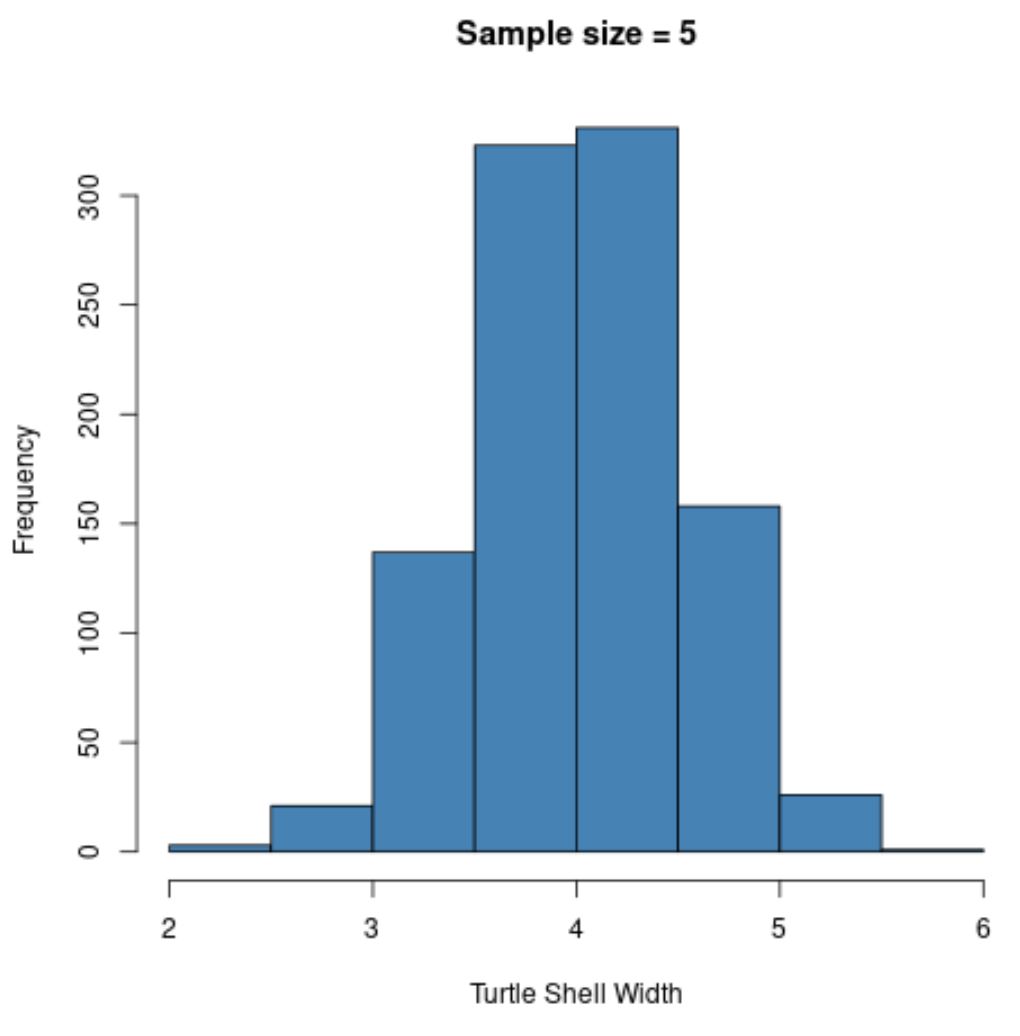
Merk op dat de steekproefverdeling van de steekproefgemiddelden normaal verdeeld lijkt, ook al was de verdeling waaruit de steekproeven voortkwamen niet normaal verdeeld.

Noteer ook het steekproefgemiddelde en de steekproefstandaarddeviatie voor deze steekproefverdeling:

• x̄ : 4,008
• s : 0,517

Stel nu dat we de steekproefgrootte die we gebruiken vergroten van n=5 naar n=30 en het histogram van de steekproefgemiddelden opnieuw creëren:

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

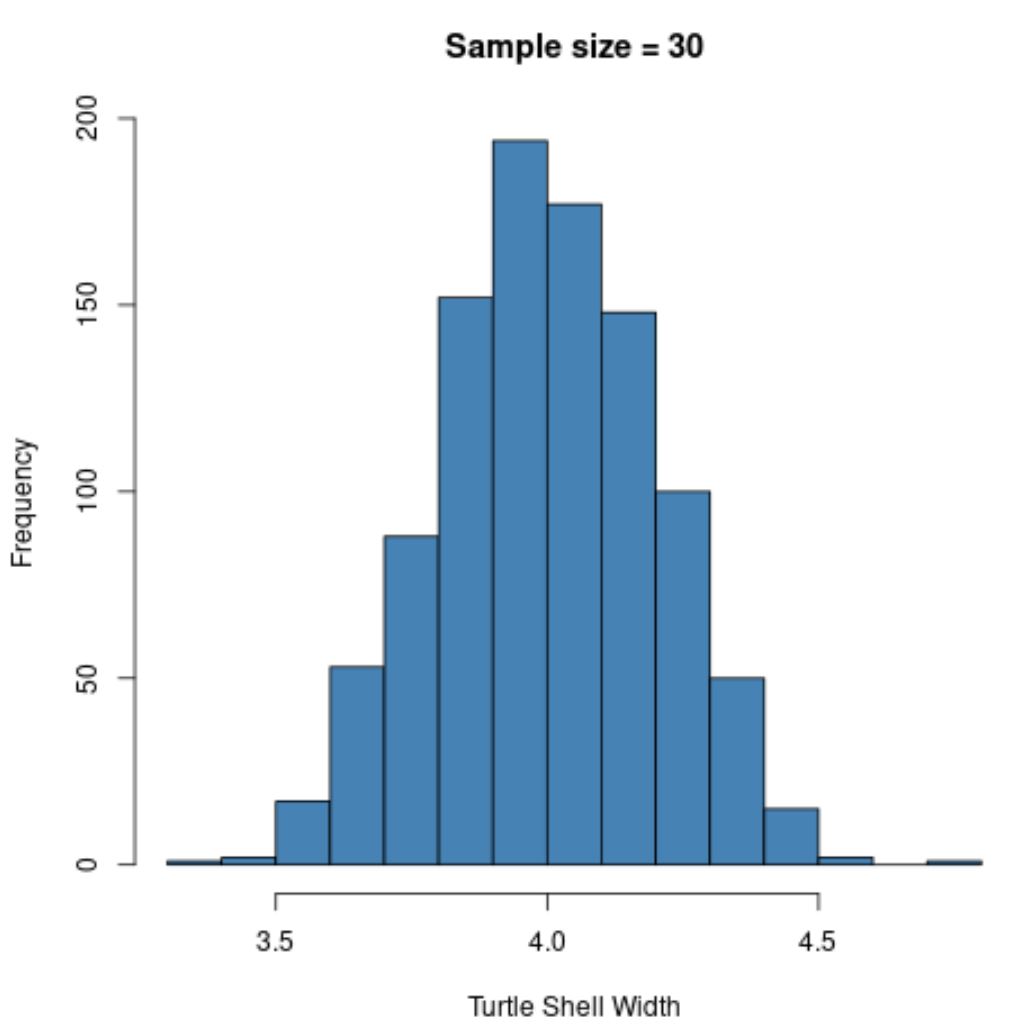
De steekproefverdeling is weer normaal verdeeld , maar de standaardafwijking van de steekproef is nog kleiner:

• s : 0,200

Dit komt omdat we een grotere steekproefomvang (n=30) hebben gebruikt in vergelijking met het vorige voorbeeld (n=5), waardoor de standaardafwijking van de steekproefgemiddelden nog kleiner is.

Als we steeds grotere steekproeven blijven gebruiken, zullen we merken dat de standaarddeviatie van de steekproef steeds kleiner wordt.

Dit illustreert de centrale limietstelling in de praktijk.

Aanvullende bronnen

De volgende bronnen bieden aanvullende informatie over de centrale limietstelling:

Een inleiding tot de centrale limietstelling
Centrale limietstelling rekenmachine
5 voorbeelden van het gebruik van de centrale limietstelling in het echte leven