Hoe de centrale limietstelling op de ti-84 rekenmachine toe te passen

De centrale limietstelling stelt dat de steekproefverdeling van een steekproefgemiddelde bij benadering normaal is als de steekproefomvang groot genoeg is, zelfs als de populatieverdeling niet normaal is.

De centrale limietstelling stelt ook dat de steekproefverdeling de volgende eigenschappen zal hebben:

1. Het gemiddelde van de steekproefverdeling zal gelijk zijn aan het gemiddelde van de populatieverdeling:

x = µ

2. De standaardafwijking van de steekproefverdeling is gelijk aan de standaardafwijking van de populatie gedeeld door de steekproefomvang:

s = σ / √n

Om de waarschijnlijkheden gerelateerd aan het steekproefgemiddelde op een TI-84-rekenmachine te vinden, kunnen we de functie normalcdf() gebruiken met de volgende syntaxis:

 normalcdf (lower value, upper value, x , s/√ n )

Goud:

• x : steekproefgemiddelden
• s : standaardafwijking van het monster
• n : steekproefomvang

Om toegang te krijgen tot deze functie op een TI-84-rekenmachine, drukt u eenvoudigweg op 2nd en vervolgens op VARS. Blader vervolgens naar normalcdf ( en druk op ENTER .

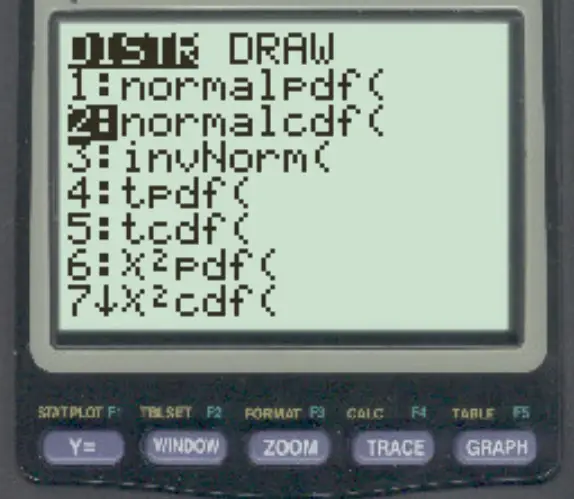
De volgende voorbeelden laten zien hoe u deze functie in de praktijk kunt gebruiken.

Voorbeeld 1: Vind de waarschijnlijkheid tussen twee waarden

Een verdeling heeft een gemiddelde van 70 en een standaarddeviatie van 7. Als we een willekeurige steekproef met een grootte van n = 35 selecteren, bepalen we de waarschijnlijkheid dat het steekproefgemiddelde tussen 68 en 72 ligt.

We kunnen de volgende syntaxis gebruiken op de TI-84:

 normalcdf (68, 72, 70, 7/√ 35 ) 

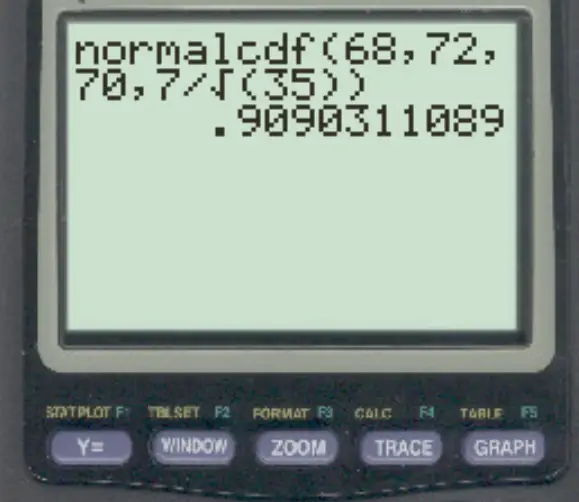
De kans dat het steekproefgemiddelde tussen 68 en 72 ligt, is 0,909 .

Voorbeeld 2: Een waarschijnlijkheid vinden die groter is dan een waarde

Een verdeling heeft een gemiddelde van 50 en een standaarddeviatie van 4. Als we een willekeurige steekproef met een grootte van n = 30 selecteren, bepalen we de kans dat het steekproefgemiddelde groter is dan 48.

We kunnen de volgende syntaxis gebruiken op de TI-84:

 normalcdf (48, E99, 50, 4/√ 30 )

Opmerking: U kunt toegang krijgen tot het “E”-symbool door op 2 te drukken en vervolgens op de knop , te drukken.

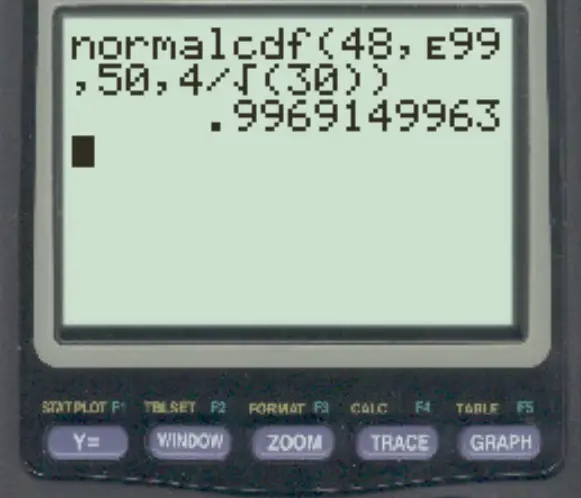
De kans dat het steekproefgemiddelde groter is dan 48 is 0,9969 .

Voorbeeld 3: Een waarschijnlijkheid vinden die kleiner is dan een waarde

Een verdeling heeft een gemiddelde van 20 en een standaarddeviatie van 3. Als we een willekeurige steekproef met een grootte van n = 40 selecteren, bepalen we de kans dat het steekproefgemiddelde kleiner is dan 19.

We kunnen de volgende syntaxis gebruiken op de TI-84:

 normalcdf (-E99, 19, 20, 3/√ 40 ) 

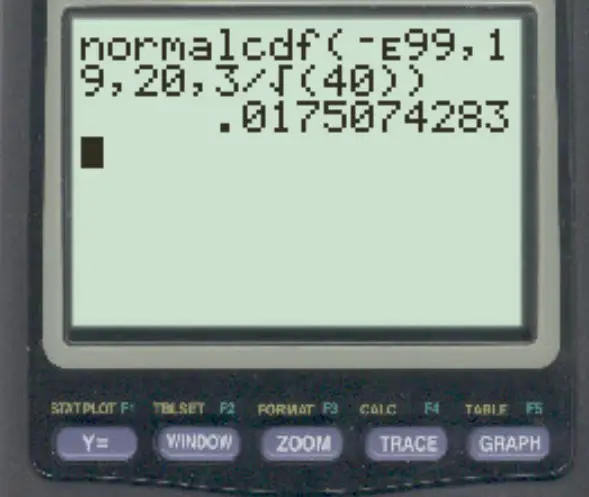
De kans dat het steekproefgemiddelde kleiner is dan 19 is 0,0175 .

Aanvullende bronnen

Een inleiding tot de centrale limietstelling
Centrale limietstelling rekenmachine
Hoe de centrale limietstelling in Excel toe te passen
Centrale limietstelling: de vier voorwaarden waaraan moet worden voldaan