Hoe de stelling van chebyshev in excel toe te passen

De stelling van Chebyshev stelt dat voor elk getal k groter dan 1, ten minste 1 – 1/k ² van de gegevenswaarden in elke getrainde verdeling binnen k standaardafwijkingen van het gemiddelde ligt.

Voor elke gevormde verdeling zal bijvoorbeeld minimaal 1 – 1/3 ² = 88,89% van de waarden in de verdeling binnen 3 standaarddeviaties van het gemiddelde vallen.

Deze tutorial demonstreert verschillende voorbeelden van het toepassen van de stelling van Chebyshev in Excel.

Voorbeeld 1: Gebruik de stelling van Chebyshev om te bepalen welk percentage van de waarden tussen 30 en 70 zal vallen voor een dataset met een gemiddelde van 50 en een standaarddeviatie van 10.

Bepaal eerst de waarde van k. We kunnen dit doen door te bepalen hoeveel standaarddeviaties tussen 30 en 70 van het gemiddelde liggen:

(30 – gemiddelde) / standaarddeviatie = (30 – 50) / 10 = -20 / 10 = -2

(70 – gemiddelde) / standaarddeviatie = (70 – 50) / 10 = 20 / 10 = 2

Waarden 30 en 70 zijn respectievelijk 2 standaarddeviaties onder en boven het gemiddelde. Dus k = 2 .

We kunnen dan de volgende formule in Excel gebruiken om het minimale percentage waarden te vinden dat binnen 2 standaarddeviaties van het gemiddelde voor deze dataset valt:

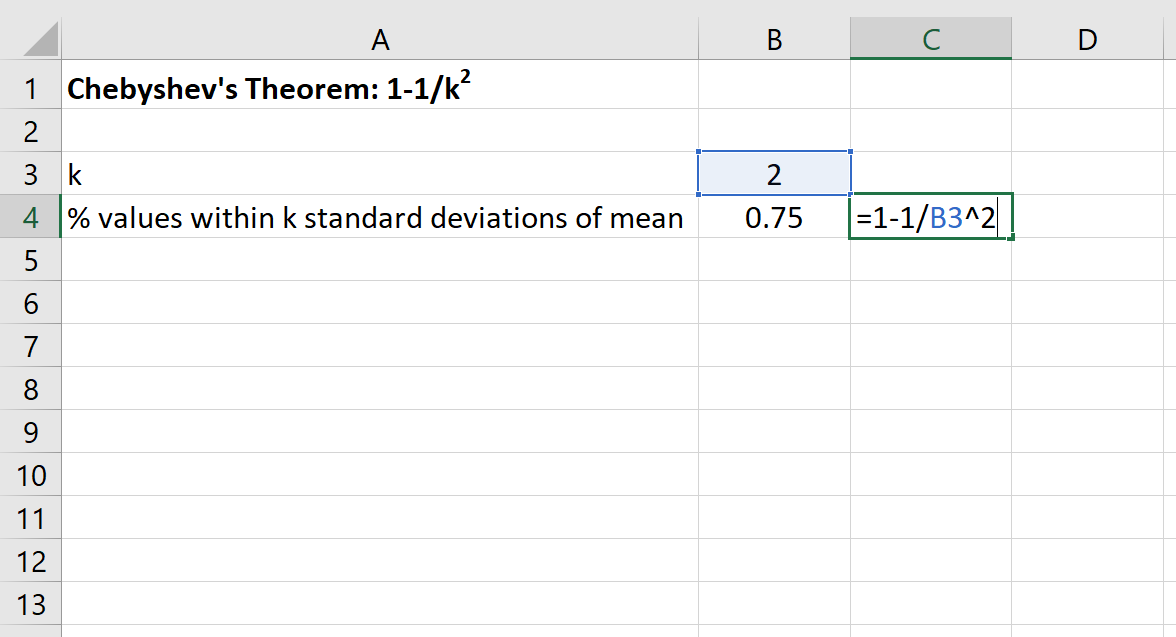
Het percentage waarden tussen 30 en 70 voor deze dataset zal minimaal 75% zijn.

Voorbeeld 2: Gebruik de stelling van Chebyshev om te bepalen welk percentage van de waarden tussen 20 en 50 zal vallen voor een dataset met een gemiddelde van 35 en een standaarddeviatie van 5.

Bepaal eerst de waarde van k. We kunnen dit doen door te bepalen hoeveel standaarddeviaties tussen 20 en 50 van het gemiddelde liggen:

(20 – gemiddelde) / standaarddeviatie = (20 – 35) / 5 = -15 / 5 = -3

(50 – gemiddelde) / standaarddeviatie = (50 – 35) / 5 = 15 / 5 = 3

De waarden 20 en 50 zijn respectievelijk 3 standaarddeviaties onder en boven het gemiddelde. Dus k = 3 .

We kunnen dan de volgende formule in Excel gebruiken om het minimale percentage waarden te vinden dat binnen 3 standaarddeviaties van het gemiddelde voor deze dataset valt:

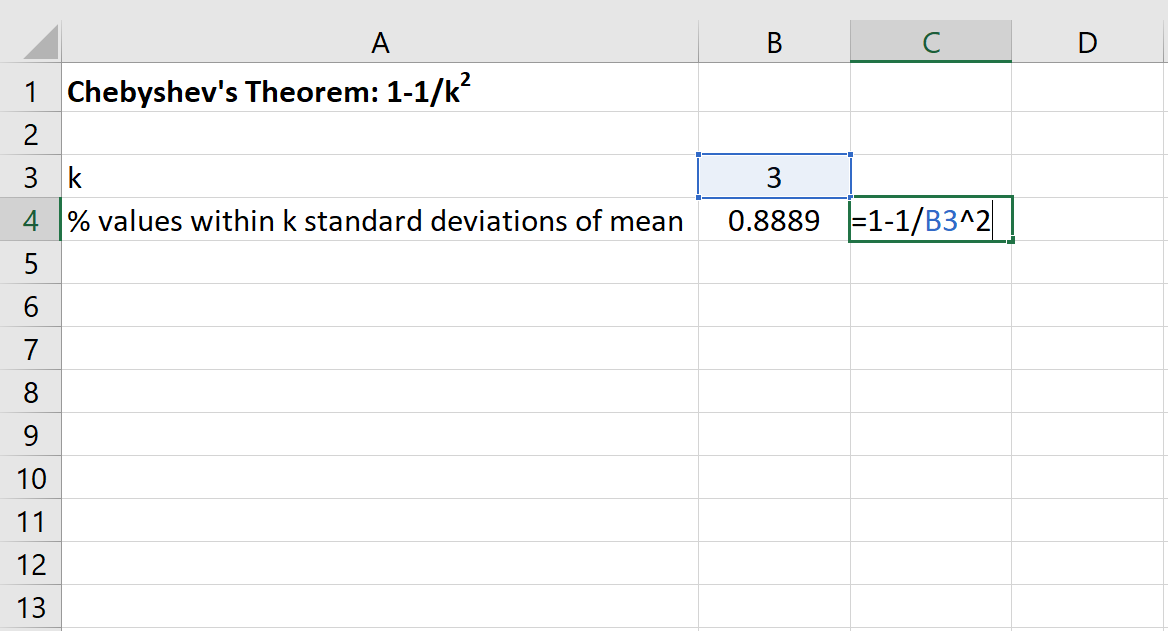
Het percentage waarden tussen 20 en 50 voor deze dataset zal minimaal 88,89% zijn.

Voorbeeld 3: Gebruik de stelling van Chebyshev om te bepalen welk percentage van de waarden tussen 80 en 120 zal vallen voor een dataset met een gemiddelde van 100 en een standaarddeviatie van 5.

Bepaal eerst de waarde van k. We kunnen dit doen door te bepalen hoeveel standaarddeviaties tussen 80 en 120 van het gemiddelde liggen:

(80 – gemiddelde) / standaarddeviatie = (80 – 100) / 5 = -20 / 5 = -4

(120 – gemiddelde) / standaarddeviatie = (120 – 100) / 5 = 20 / 5 = 4

De waarden 80 en 120 zijn respectievelijk 4 standaarddeviaties onder en boven het gemiddelde. Dus k = 4 .

We kunnen dan de volgende formule in Excel gebruiken om het minimale percentage waarden te vinden dat binnen 4 standaarddeviaties van het gemiddelde voor deze dataset valt:

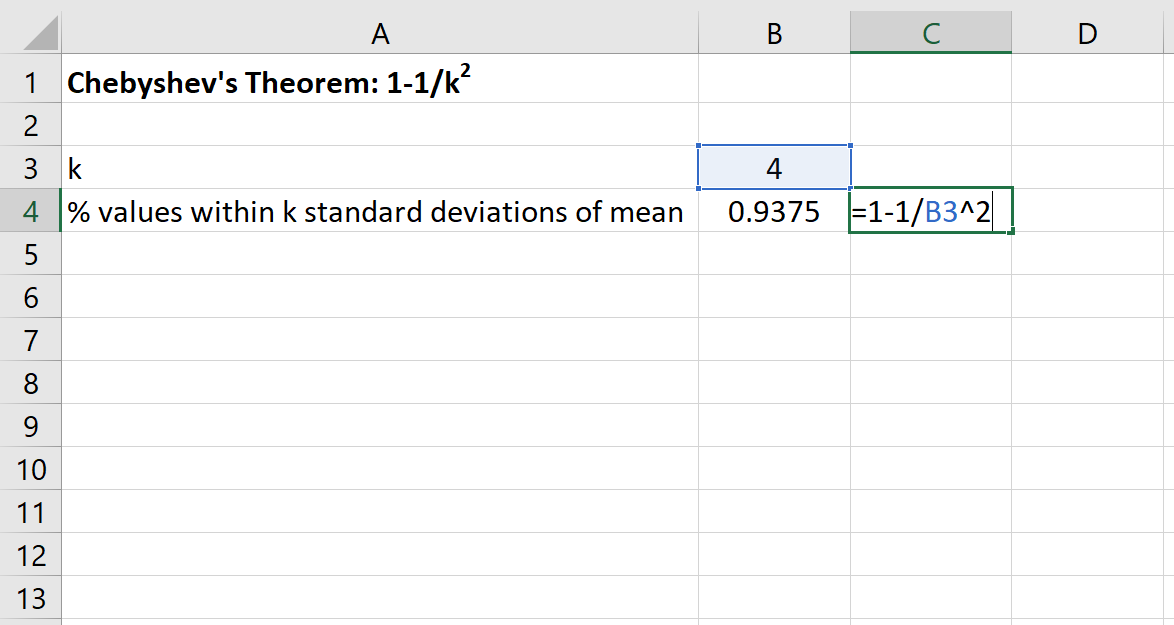
Het percentage waarden tussen 80 en 120 voor deze dataset zal minimaal 93,75% zijn.