Chi-kwadraat fittest op een ti-84-rekenmachine

Een chikwadraat-goodness-of-fit-test wordt gebruikt om te bepalen of een categorische variabele al dan niet een hypothetische verdeling volgt.

In deze tutorial wordt uitgelegd hoe u een chikwadraat-fittest uitvoert op een TI-84-rekenmachine.

Voorbeeld: Chi-kwadraat-fittest op een TI-84-rekenmachine

Een winkeleigenaar vertelt dat er elke dag van de week evenveel klanten naar zijn winkel komen. Om deze hypothese te testen, registreert een onafhankelijke onderzoeker het aantal klanten dat in een bepaalde week de winkel binnenkomt en ontdekt het volgende:

• Maandag: 50 klanten
• Dinsdag: 60 klanten
• Woensdag: 40 klanten
• Donderdag: 47 klanten
• Vrijdag: 53 klanten

We zullen de volgende stappen gebruiken om een chikwadraat-goodness-of-fit-test uit te voeren om te bepalen of de gegevens consistent zijn met de claim van de winkeleigenaar.

Stap 1: Voer de gegevens in.

Eerst voeren we de gegevenswaarden in voor het verwachte aantal klanten per dag en het waargenomen aantal klanten per dag. Druk op Stat en vervolgens op BEWERKEN . Vul de volgende waarden in voor het waargenomen aantal klanten in kolom L1 en de waarden voor het verwachte aantal klanten in kolom L2:

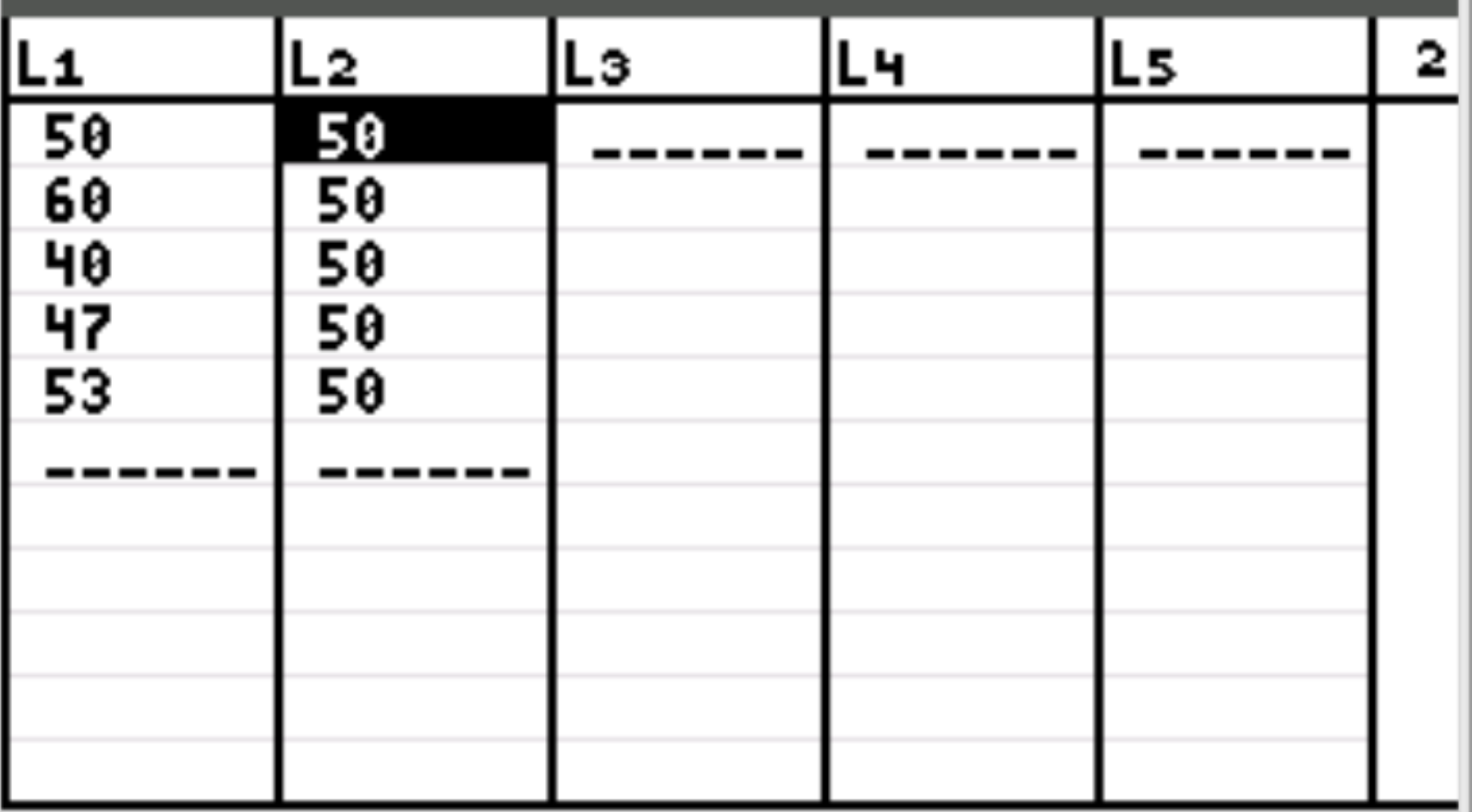
Let op: Er waren in totaal 250 klanten. Dus als de winkeleigenaar verwacht dat er elke dag een gelijk aantal klanten de winkel binnenkomt, zijn dat 50 klanten per dag.

Stap 2: Voer de chikwadraat-goodness-of-fit-test uit.

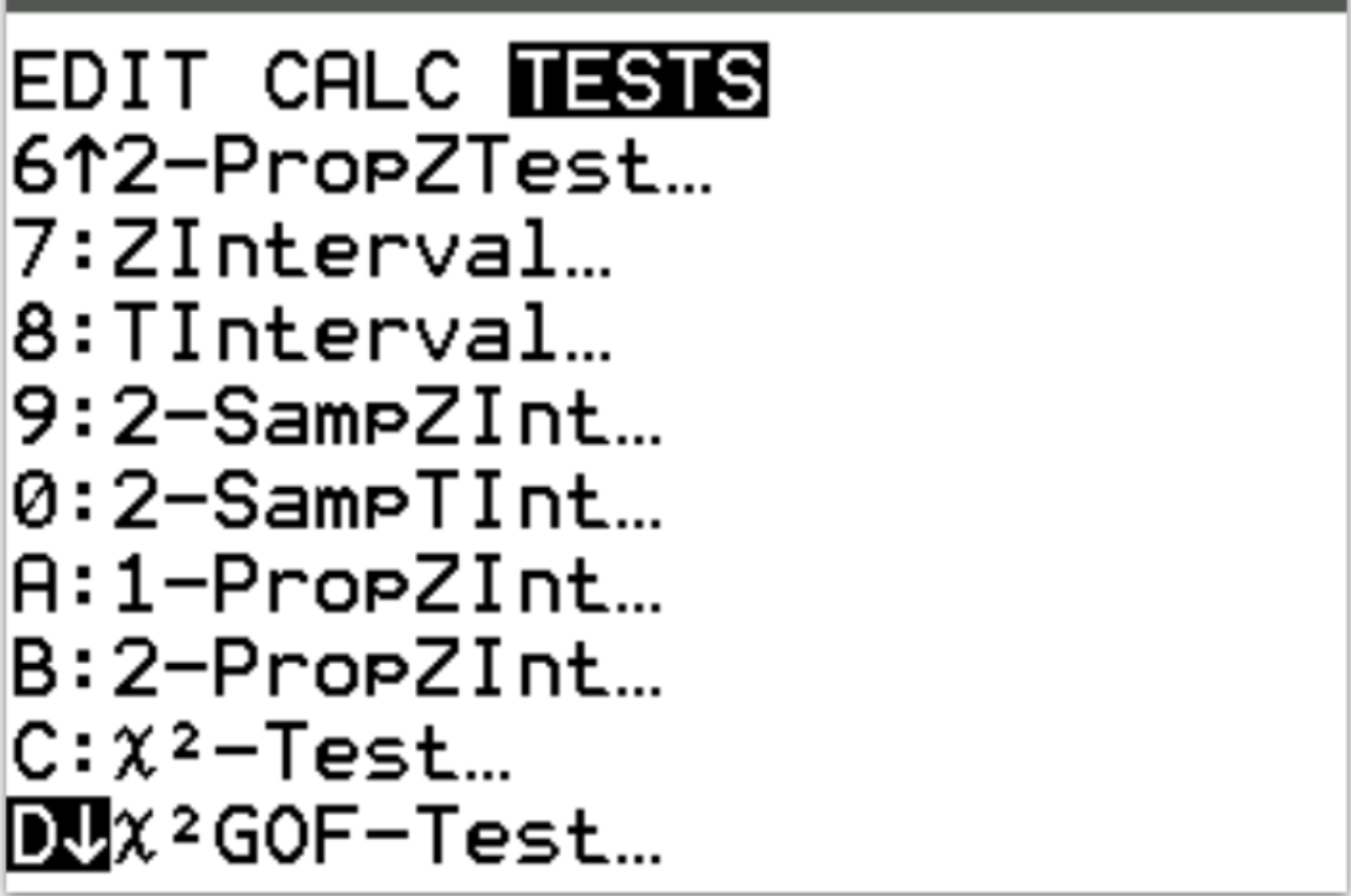
Vervolgens voeren we de chi-kwadraat goodness-of-fit test uit. Druk op Stat en scroll vervolgens naar TESTS . Blader vervolgens omlaag naar X ² GOF-Test en druk op Enter .

Voor Waargenomen kiest u de L1-lijst. Kies voor Expected de L2-lijst. Voor df (vrijheidsgraden) voert u #categories – 1 in. In ons geval hebben we 5-1 = 4. Markeer vervolgens Berekenen en druk op Enter .

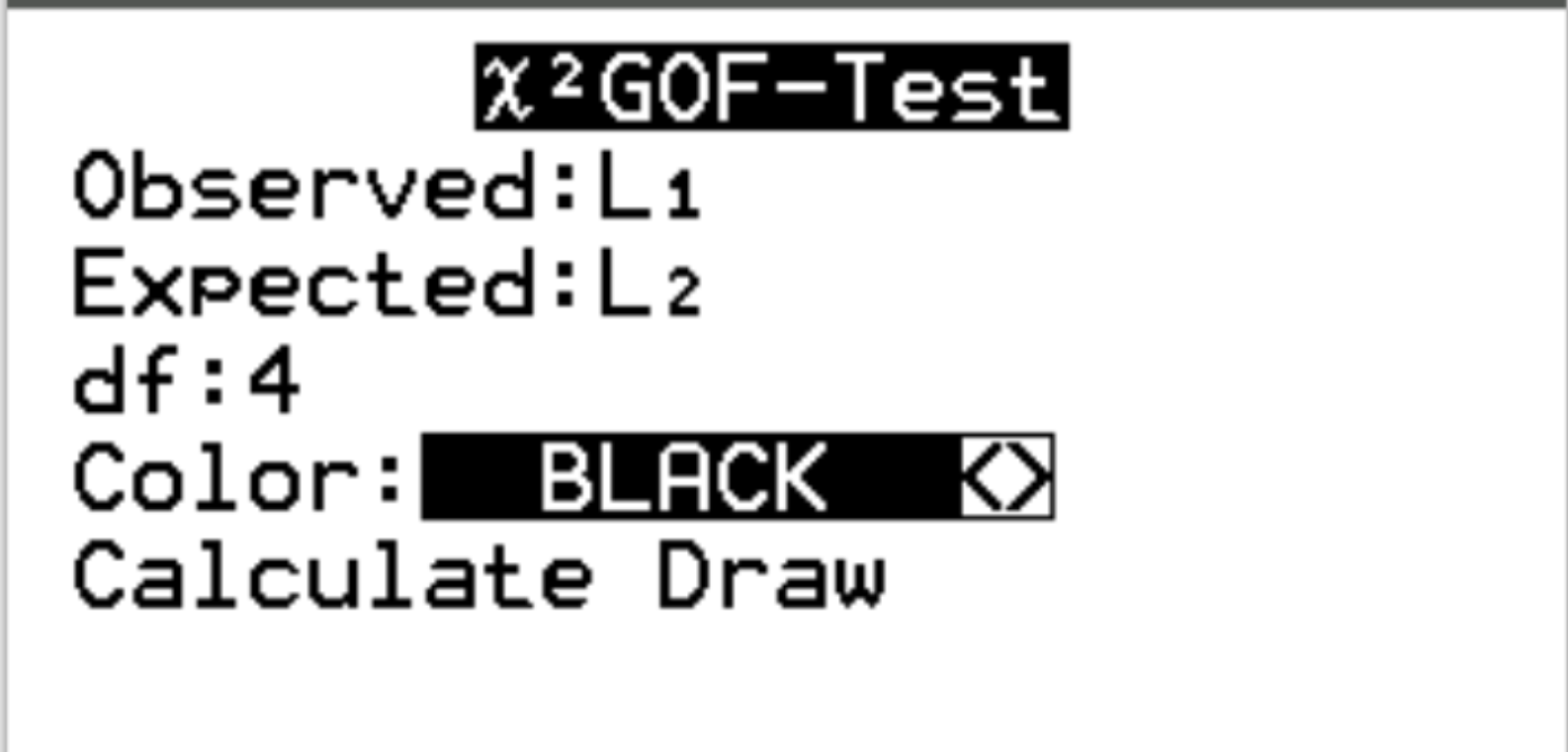
De volgende uitvoer verschijnt automatisch:

Stap 3: Interpreteer de resultaten.

De ^X2- teststatistiek voor de test is 4,36 en de overeenkomstige p-waarde is 0,3595 . Omdat deze p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen. Dit betekent dat we niet genoeg bewijs hebben om te zeggen dat de werkelijke distributie van klanten verschilt van die gerapporteerd door de winkeleigenaar.