Hoe u een chi square goodness of fit-test uitvoert in spss
Een chikwadraat-goodness-of-fit-test wordt gebruikt om te bepalen of een categorische variabele al dan niet een hypothetische verdeling volgt.
In deze tutorial wordt uitgelegd hoe u een chikwadraat-goodness-of-fit-test uitvoert in SPSS.
Voorbeeld: Chi-kwadraat goodness-of-fit-test in SPSS
Een winkeleigenaar vertelt dat er elke dag van de week evenveel klanten naar zijn winkel komen. Om deze hypothese te testen, registreert een onderzoeker het aantal klanten dat in een bepaalde week de winkel binnenkomt en ontdekt het volgende:
- Maandag: 50 klanten
- Dinsdag: 60 klanten
- Woensdag: 40 klanten
- Donderdag: 47 klanten
- Vrijdag: 53 klanten
Gebruik de volgende stappen om een chikwadraat-goodness-of-fit-test uit te voeren in SPSS om te bepalen of de gegevens consistent zijn met de claim van de winkeleigenaar.
Stap 1: Voer de gegevens in.
Voer eerst de gegevens in SPSS in het volgende formaat in:
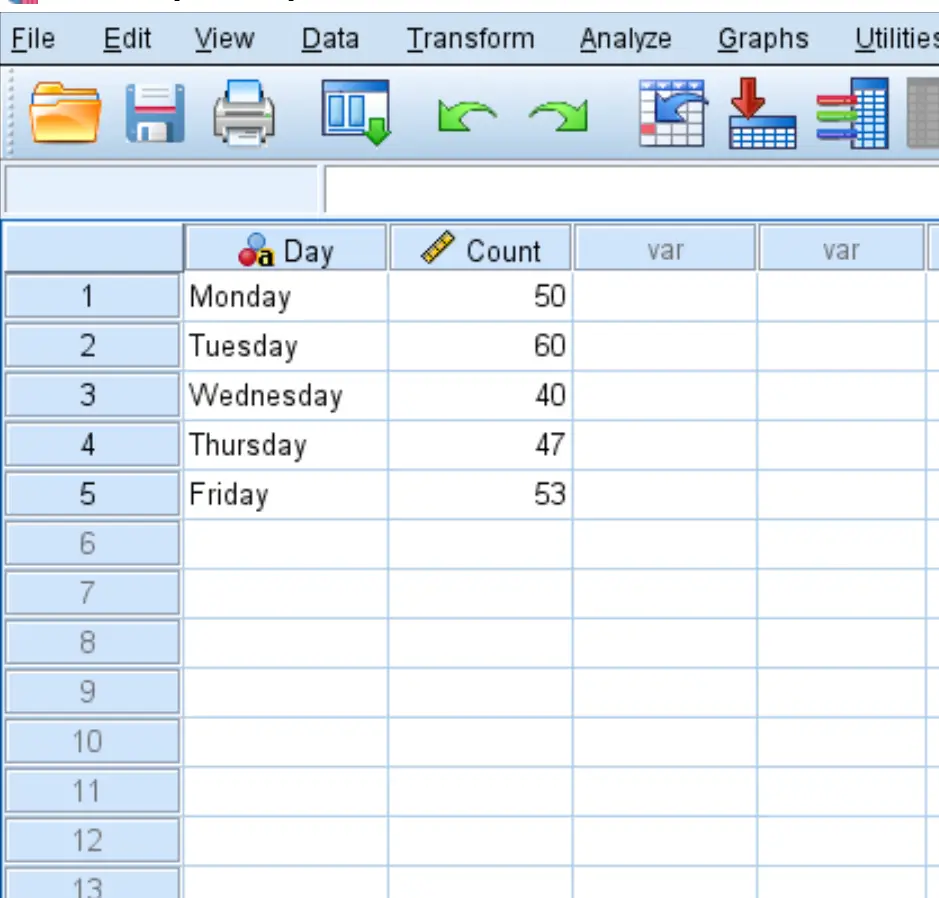
Stap 2: Gebruik verzwaarde dozen.
Om de test correct te laten werken, moeten we SPSS vertellen dat de variabele ‚Dag‘ moet worden gewogen door de variabele ‚Aantal‘.
Klik op het tabblad Gegevens en klik vervolgens op Gewichtsgevallen :
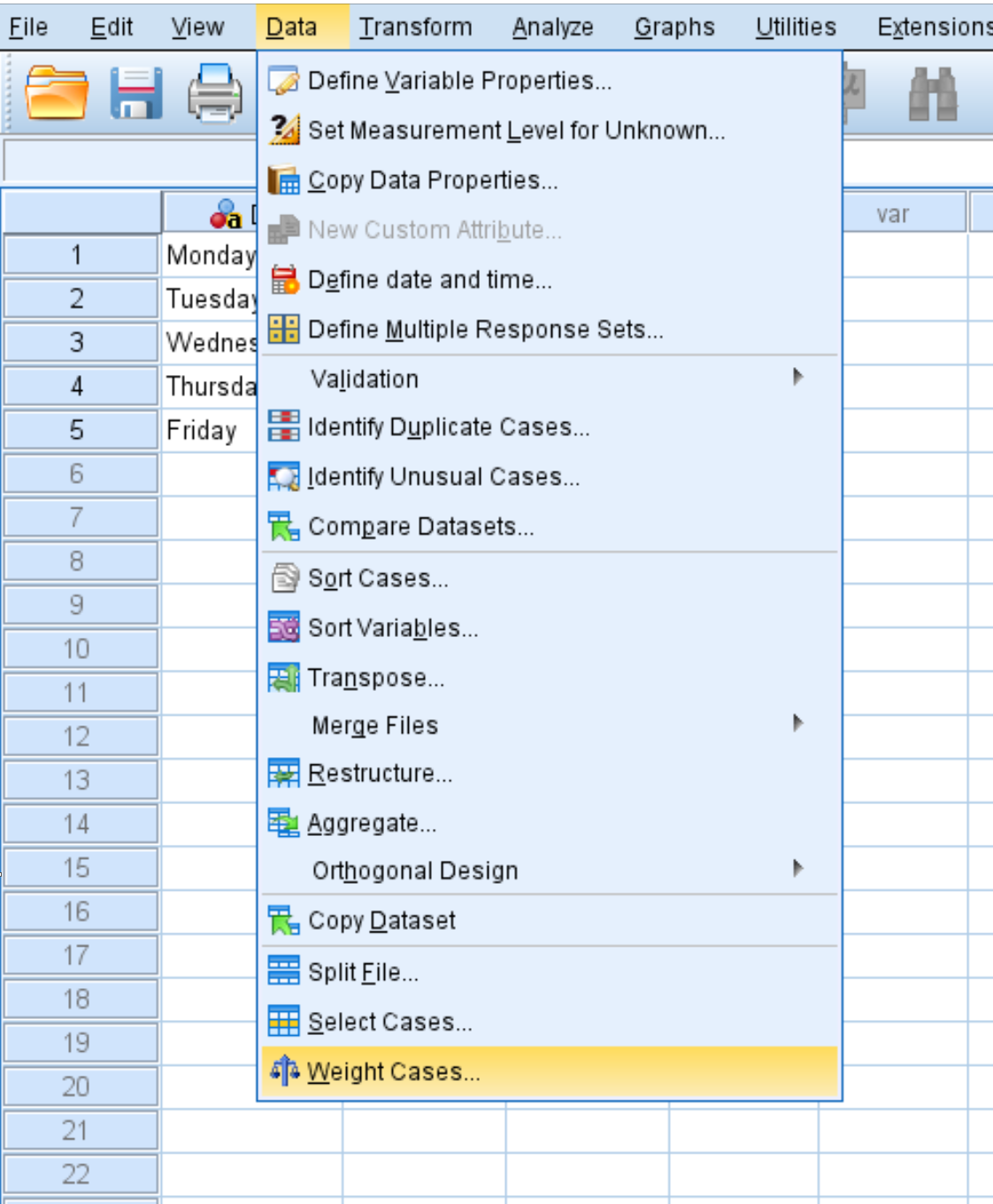
Sleep in het nieuwe venster dat verschijnt de variabele Count naar het gebied met de naam Testvariabelenlijst. Klik vervolgens op OK .
Stap 3: Voer de chikwadraat-goodness-of-fit-test uit.
Klik op het tabblad Analyseren , vervolgens op Niet-parametrische tests , vervolgens op Legacy Dialogs en vervolgens op Chi Square :
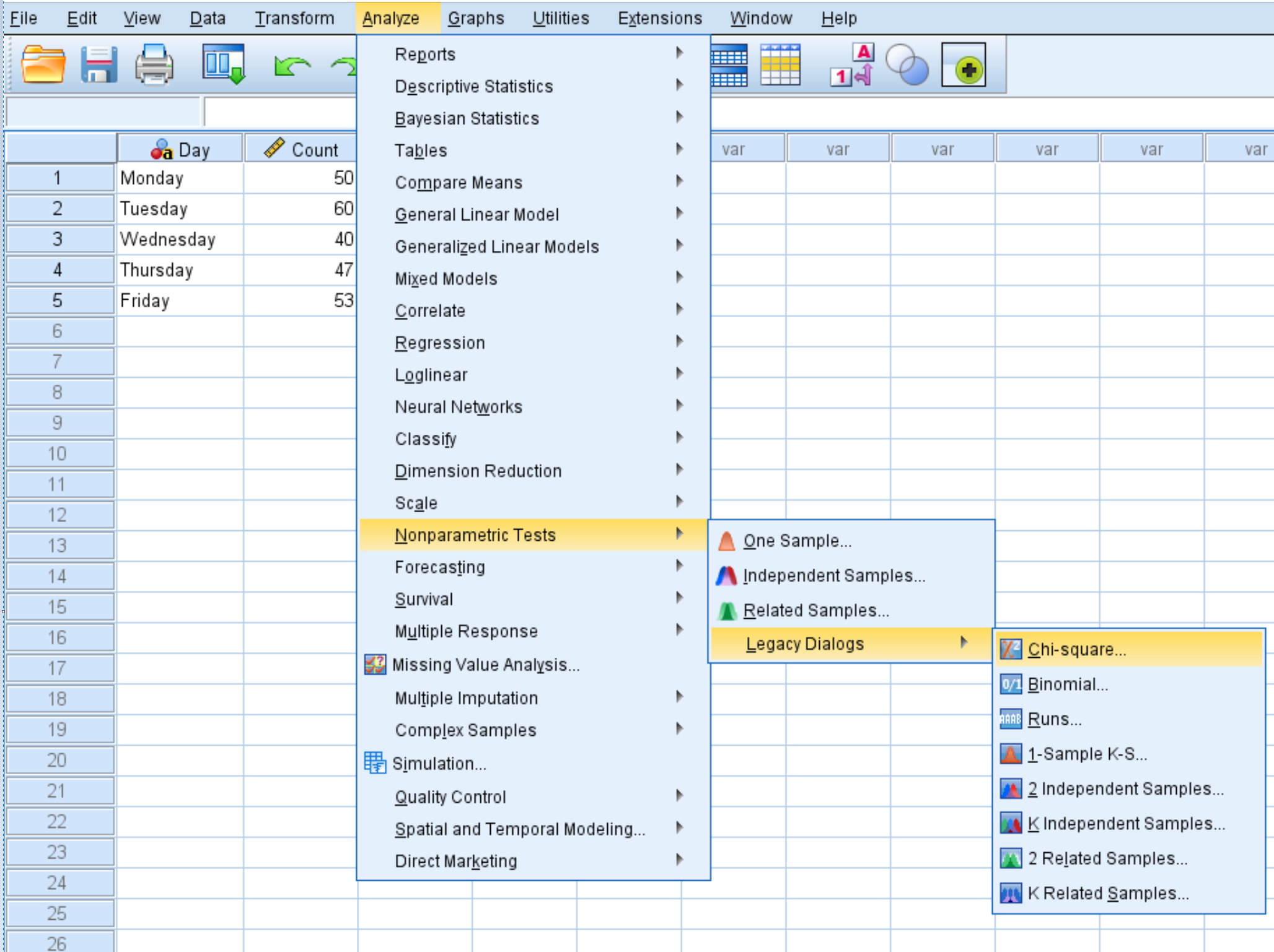
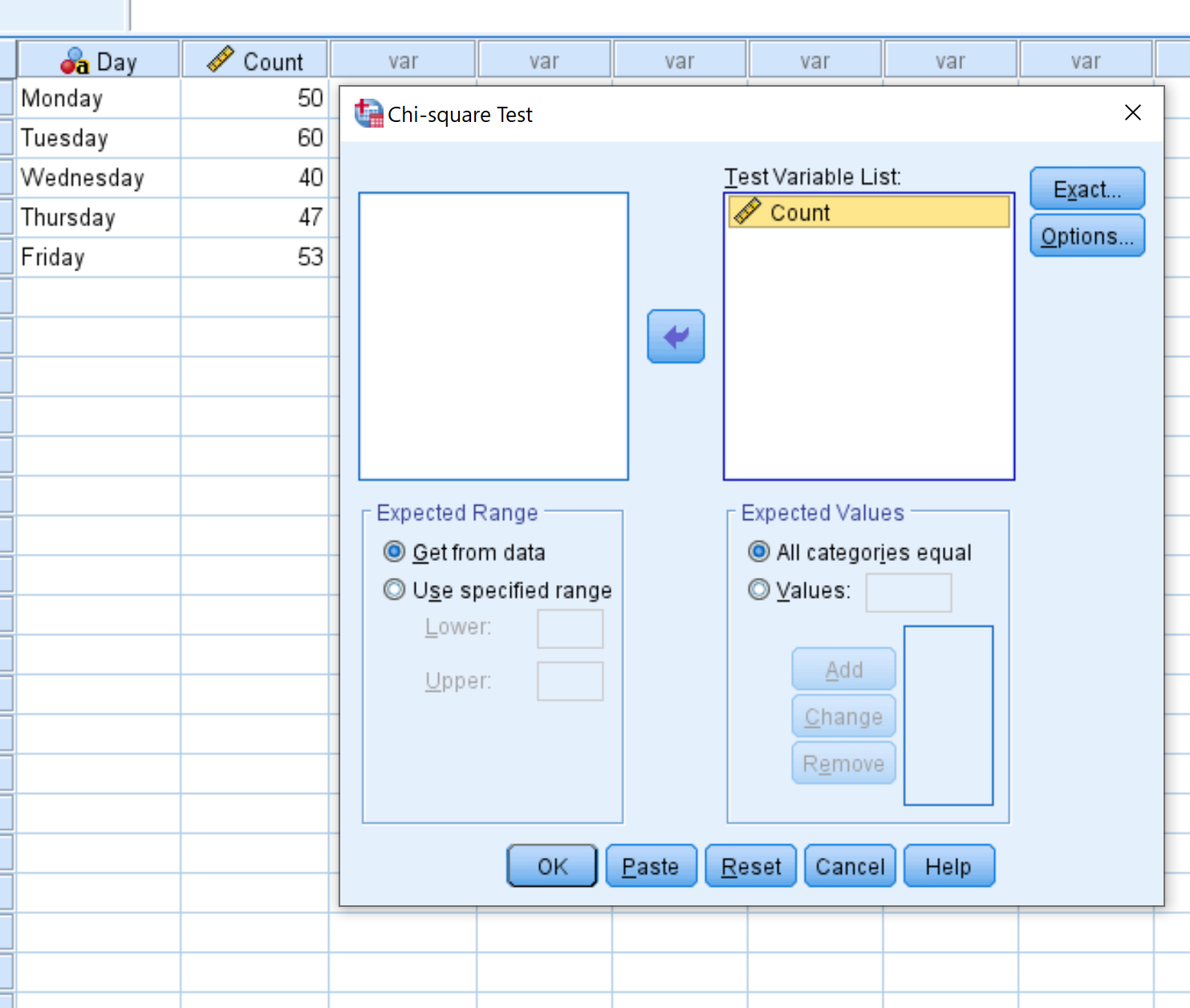
Sleep in het nieuwe venster dat verschijnt de variabele Count naar het gebied met de naam Testvariabelenlijst.
Laat het label naast Alle categorieën gelijk aangevinkt, aangezien elk van onze categorieën (dat wil zeggen de dagen van de week) elke dag hetzelfde verwachte aantal bezoekers heeft. Klik vervolgens op OK .

Stap 4: Interpreteer de resultaten .
Zodra u op OK klikt, verschijnen de chikwadraat-goodness-of-fit-testresultaten:
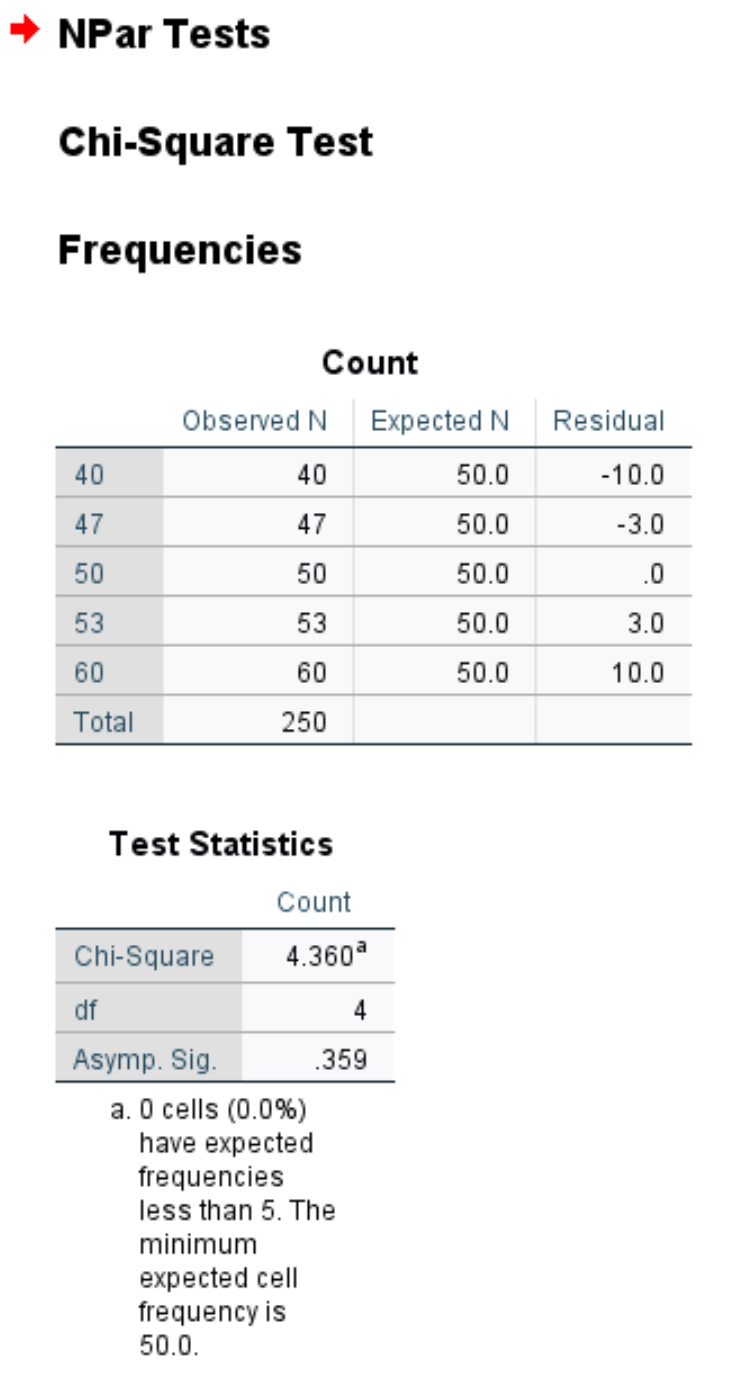
De eerste tabel toont het waargenomen en verwachte aantal klanten per dag van de week, evenals het residu (dat wil zeggen het verschil) tussen het waargenomen en het verwachte aantal.
De tweede tabel toont de volgende cijfers:
Chi-kwadraat: De chi-kwadraat-teststatistiek, die 4,36 is.
df: De vrijheidsgraden, berekend als #categories-1 = 5-1 = 4.
Asympt. Sig: De p-waarde die overeenkomt met een Chi-kwadraatwaarde van 4,36 met 4 vrijheidsgraden, namelijk 0,359. Deze waarde kan ook worden gevonden met behulpvan de chi-kwadraatscore naar P-waardecalculator.
Omdat de p-waarde (0,359) niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen. Dit betekent dat we niet genoeg bewijs hebben om te zeggen dat de werkelijke distributie van klanten verschilt van die gerapporteerd door de winkeleigenaar.