Chi-kwadraatverdeling

Von Dr.benjamin anderson August 4, 2023 Waarschijnlijkheid Keine Kommentare

In dit artikel wordt uitgelegd wat de chikwadraatverdeling is en waarvoor deze wordt gebruikt. Daarnaast vindt u de chikwadraatverdelingsgrafiek en zijn eigenschappen.

Wat is de chikwadraatverdeling?

De Chi-kwadraatverdeling is een kansverdeling waarvan het symbool χ² is. Preciezer gezegd: de Chi-kwadraatverdeling is de som van het kwadraat van k onafhankelijke willekeurige variabelen met een normale verdeling.

De Chi-kwadraatverdeling heeft dus k vrijheidsgraden. Daarom heeft een Chi-kwadraatverdeling evenveel vrijheidsgraden als de som van de kwadraten van de normaal verdeelde variabelen die deze vertegenwoordigt.

$\displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}$

De Chi-kwadraatverdeling wordt ook wel de Pearson-verdeling genoemd.

Opgemerkt moet worden dat de Chi-kwadraatverdeling een speciaal geval is van de gammaverdeling.

De chikwadraatverdeling wordt veel gebruikt bij statistische gevolgtrekkingen, bijvoorbeeld bij het testen van hypothesen en betrouwbaarheidsintervallen. We zullen hieronder zien wat de toepassingen zijn van dit type kansverdeling.

Chi-kwadraatverdelingsgrafiek

Zodra we de definitie van de Chi-kwadraatverdeling zien, zullen we verschillende voorbeelden van dit type verdeling grafisch weergegeven zien. Hieronder kun je zien hoe de waarschijnlijkheidsgrafiek van de chikwadraatverdeling varieert, afhankelijk van de vrijheidsgraden.

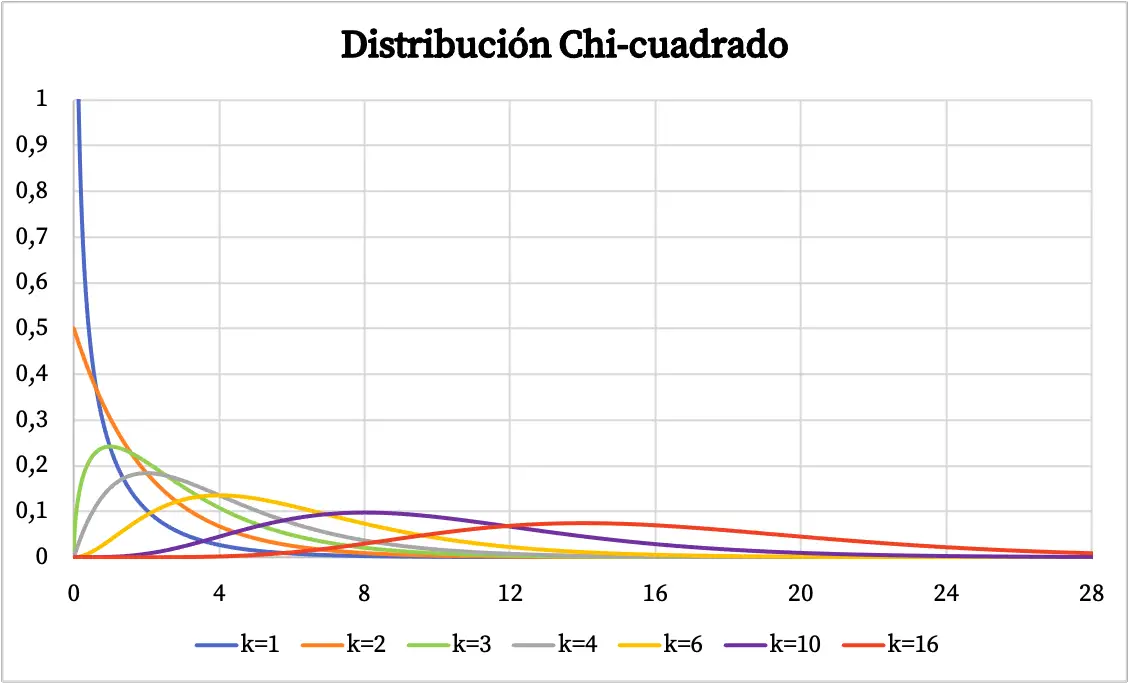
De dichtheidsfunctie van de Chi-kwadraatverdeling is weergegeven in de bovenstaande grafiek. Aan de andere kant is de grafiek van de chikwadraat cumulatieve kansverdelingsfunctie als volgt:

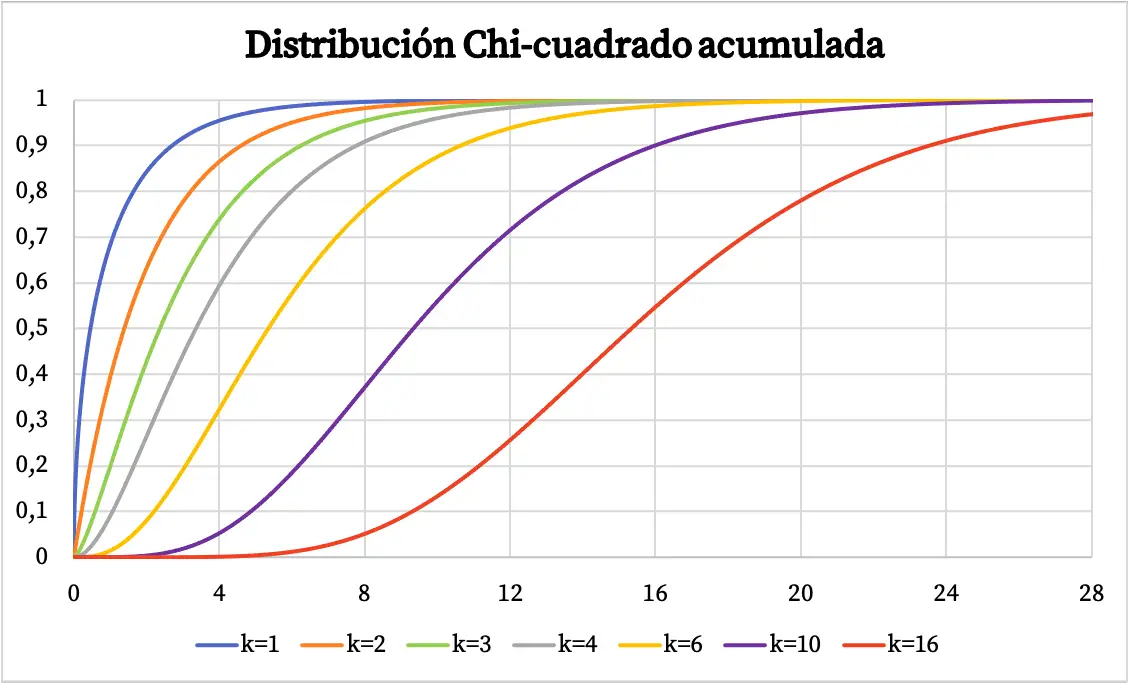
chi-kwadraat cumulatieve verdelingsgrafiek

➤ Zie: Chi-kwadraatverdelingstabel

Kenmerken van de chikwadraatverdeling

In deze sectie zullen we de belangrijkste eigenschappen van de Chi-kwadraatverdeling zien die verband houden met de waarschijnlijkheidstheorie en statistiek.

Het gemiddelde van een chikwadraatverdeling is gelijk aan de vrijheidsgraden.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}$

De variantie van een Chi-kwadraatverdeling is gelijk aan tweemaal de vrijheidsgraden van de verdeling.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}$

De modus van een chikwadraatverdeling is twee eenheden minder dan de vrijheidsgraden, zolang de verdeling meer dan één vrijheidsgraad heeft.

$Mo=k-2 \qquad \text{si } k\geq 2$

De dichtheidsfunctie van de Chi-kwadraatverdeling is nul als x=0. Voor waarden van x groter dan 0 wordt de dichtheidsfunctie van een Chi-kwadraatverdeling echter gedefinieerd door de volgende formule:

$\displaystyle P[X=x]= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

De cumulatieve verdelingsfunctie van de Chi-kwadraatverdeling wordt bepaald door de volgende formule:

$\displaystyle P[X\leq x]=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

De scheefheidscoëfficiënt van de Chi-kwadraatverdeling is de vierkantswortel van het quotiënt van acht gedeeld door het aantal vrijheidsgraden van de verdeling.

$\displaystyle A=\sqrt{\frac{8}{k}}$

De kurtosis van de Chi-kwadraatverdeling wordt berekend met behulp van de volgende uitdrukking:

$C=3+\cfrac{12}{k}$

Vanwege de centrale limietstelling kan de chikwadraatverdeling benaderd worden door een normale verdeling als k groot genoeg is.

$\displaystyle\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{\left(1,\sqrt{2/k}\right)} (x)$

Toepassingen van de chikwadraatverdeling

De chikwadraatverdeling heeft veel verschillende toepassingen in de statistiek. In feite bestaat er zelfs de chikwadraattoets die wordt gebruikt om de onafhankelijkheid tussen variabelen en de geschiktheid ervan voor een theoretische verdeling te controleren. De Chi-kwadraattoets kan bijvoorbeeld worden gebruikt om te bepalen of de gegevens van een steekproef voldoen aan een Poisson-verdeling.

Bij lineaire regressieanalyse wordt de chikwadraatverdeling ook gebruikt om het gemiddelde van een normaal verdeelde populatie te schatten en om de helling van de lineaire regressiestudielijn te schatten.

Ten slotte neemt de Chi-kwadraatverdeling ook deel aan de variantieanalyse, via zijn relatie met de Snedecor F-verdeling.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder