4 voorbeelden van het gebruik van chikwadraattoetsen in het echte leven
In de statistiek zijn er twee verschillende soorten Chi-kwadraattoetsen:
1. Chi-kwadraat goodness-of-fit-test – Wordt gebruikt om te bepalen of een categorische variabele al dan niet een hypothetische verdeling volgt.
2. De Chi-kwadraattest van onafhankelijkheid – Wordt gebruikt om te bepalen of er al dan niet een significant verband bestaat tussen twee categorische variabelen.
In dit artikel delen we verschillende voorbeelden van hoe elk van dit soort Chi-kwadraattoetsen in praktijksituaties wordt gebruikt.
Voorbeeld 1: Chi-kwadraat goodness-of-fit-test
Stel dat een winkeleigenaar beweert dat er elke dag van de week evenveel klanten naar zijn winkel komen.
Om deze hypothese te testen, registreert hij het aantal klanten dat in een bepaalde week de winkel binnenkomt en vindt hij het volgende:
- Maandag: 50 klanten
- Dinsdag: 60 klanten
- Woensdag: 40 klanten
- Donderdag: 47 klanten
- Vrijdag: 53 klanten
Hij kan een chikwadraat-goodness-of-fit-test gebruiken om te bepalen of de verdeling van de klanten die elke dag komen consistent is met zijn verdelingshypothese.
Met behulp van de chikwadraat-goodness-of-fit-testcalculator kan hij zien dat de p-waarde van de test 0,359 is.
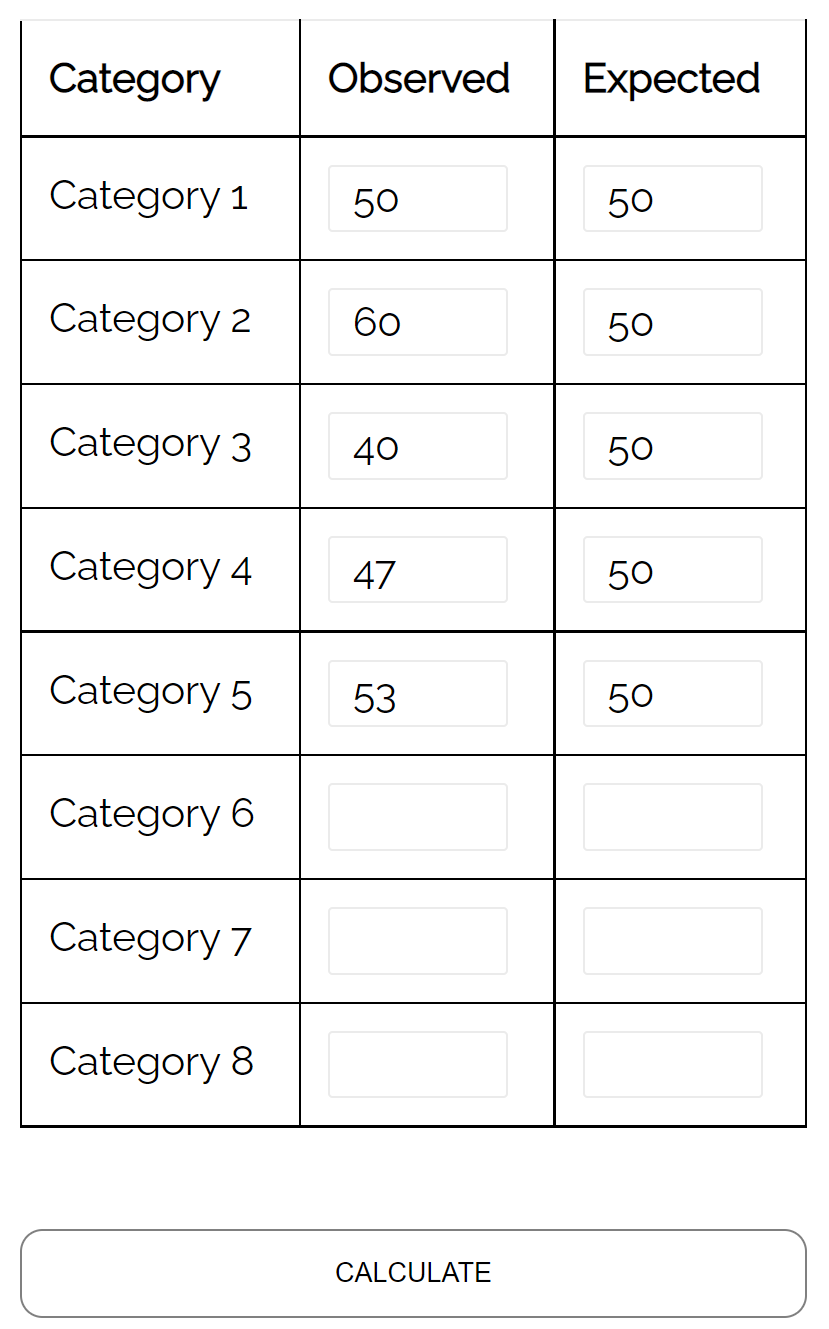

Aangezien deze p-waarde niet minder dan 0,05 bedraagt, is er niet voldoende bewijs om te beweren dat de werkelijke distributie van klanten verschilt van die welke door de winkeleigenaar wordt beweerd.
Voorbeeld 2: Chi-kwadraat goodness-of-fit-test
Stel dat een bioloog beweert dat er wekelijks een gelijk aantal van vier verschillende soorten herten een bepaald bosgebied van een bos binnenkomen.
Om deze hypothese te testen, registreert ze van elke soort herten het aantal dat in de loop van een week het bosrijke gebied binnenkomt:
- Soort #1: 22
- Soort #2: 20
- Soort #3: 23
- Soort #4: 35
Ze kan een chikwadraat-goodness-of-fit-test gebruiken om te bepalen of de verspreiding van hertensoorten die wekelijks het bosrijke gebied van het bos binnenkomen consistent is met de hypothetische verspreiding ervan.
Met behulp van de chikwadraat-goodness-of-fit-testcalculator kan ze zien dat de p-waarde voor de test 0,137 is.
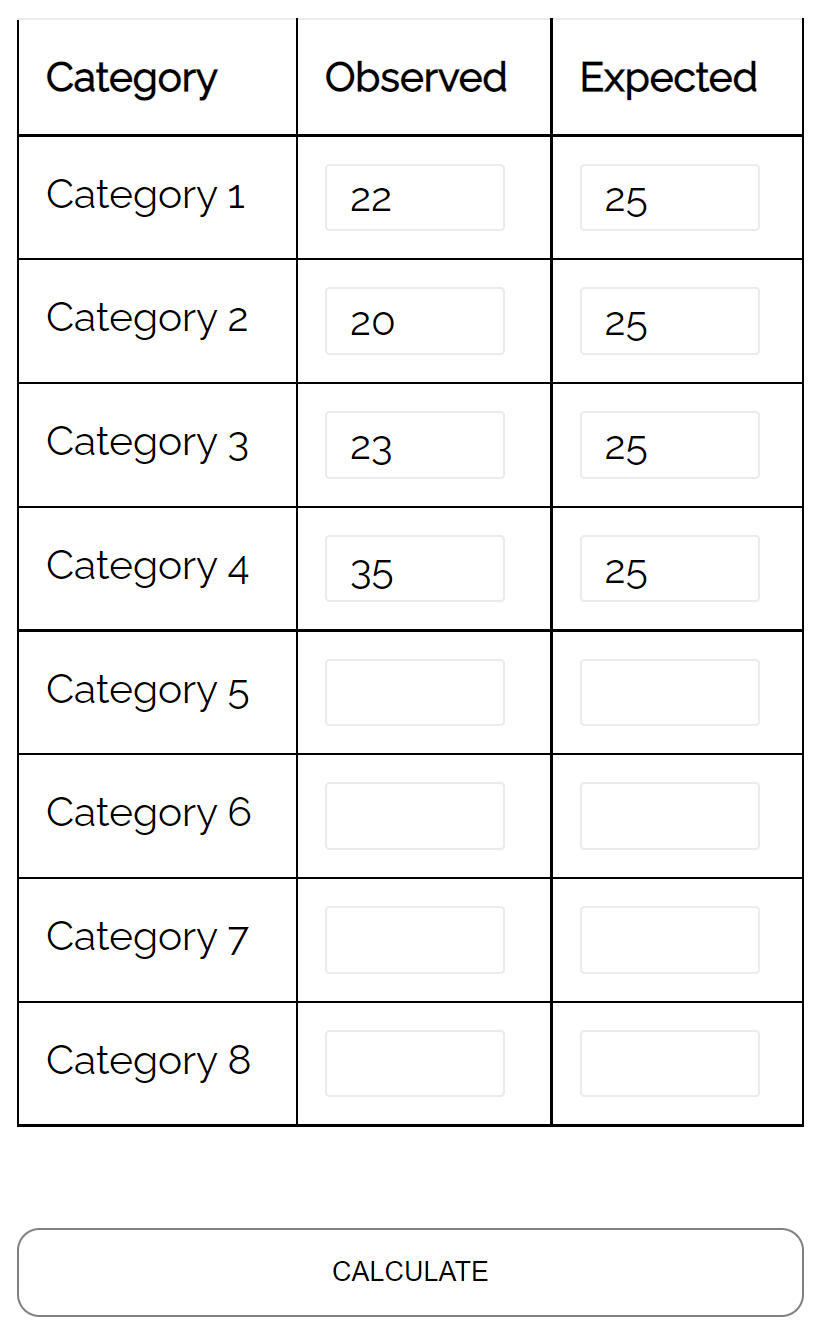
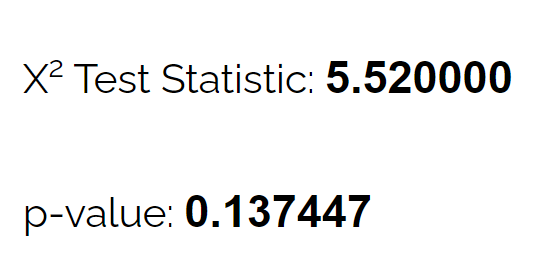
Aangezien deze p-waarde niet minder dan 0,05 bedraagt, is er niet voldoende bewijs om te beweren dat de werkelijke verspreiding van herten anders is dan die welke door de bioloog wordt beweerd.
Voorbeeld 3: Chi-kwadraat-onafhankelijkheidstest
Stel dat een beleidsmaker in een bepaalde stad wil weten of gender al dan niet verband houdt met de voorkeur van een politieke partij.
Hij besluit een eenvoudige willekeurige steekproef van 500 kiezers te nemen en hen te vragen naar hun politieke partijvoorkeur. De volgende tabel geeft de resultaten van het onderzoek weer:
| Republikeins | Democraat | Onafhankelijk | Totaal | |
| Mannelijk | 120 | 90 | 40 | 250 |
| Vrouwelijk | 110 | 95 | 45 | 250 |
| Totaal | 230 | 185 | 85 | 500 |
Het kan een chikwadraattest van onafhankelijkheid gebruiken om te bepalen of er een statistisch significant verband bestaat tussen de twee variabelen.
Met behulp van de chikwadraat-onafhankelijkheidstestcalculator kan hij zien dat de p-waarde van de test 0,649 is.
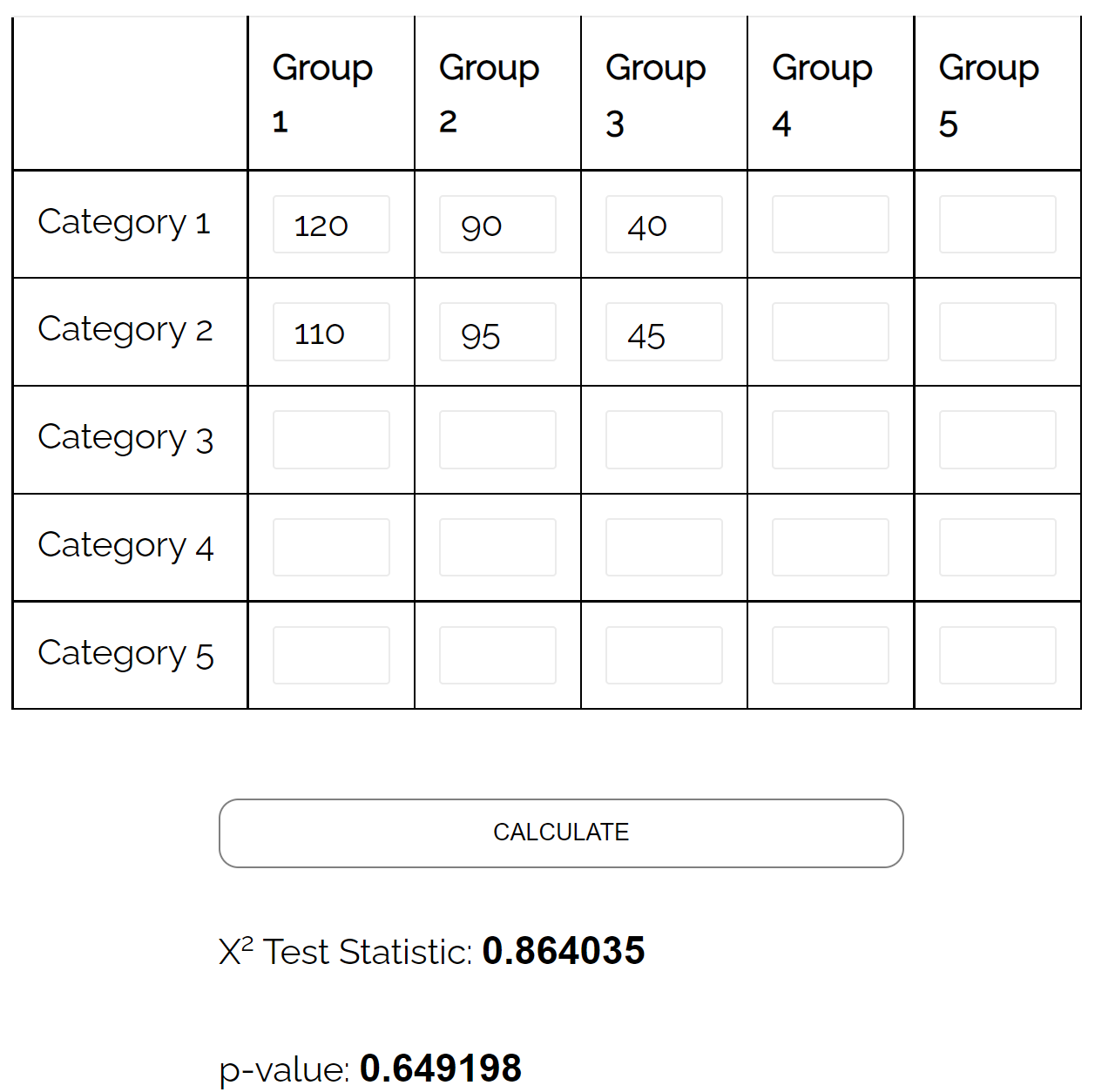
Omdat de p-waarde niet kleiner is dan 0,05, is er niet voldoende bewijs om te zeggen dat er een verband bestaat tussen geslacht en politieke partijvoorkeur.
Voorbeeld 4: Chi-kwadraat-onafhankelijkheidstest
Stel dat een onderzoeker wil weten of de burgerlijke staat al dan niet verband houdt met het opleidingsniveau.
Hij besluit een eenvoudige willekeurige steekproef van 300 personen te nemen en krijgt de volgende resultaten:
| Middelbare school | Vrijgezellen | Master of hoger | Totaal | |
| Getrouwd | 20 | 100 | 35 | 155 |
| Bachelor opleiding | 50 | 80 | 15 | 145 |
| Totaal | 70 | 180 | 50 | 300 |
Het kan een chikwadraattest van onafhankelijkheid gebruiken om te bepalen of er een statistisch significant verband bestaat tussen de twee variabelen.
Met behulp van de chikwadraat-onafhankelijkheidstestcalculator kan hij zien dat de p-waarde van de test 0,000011 is.
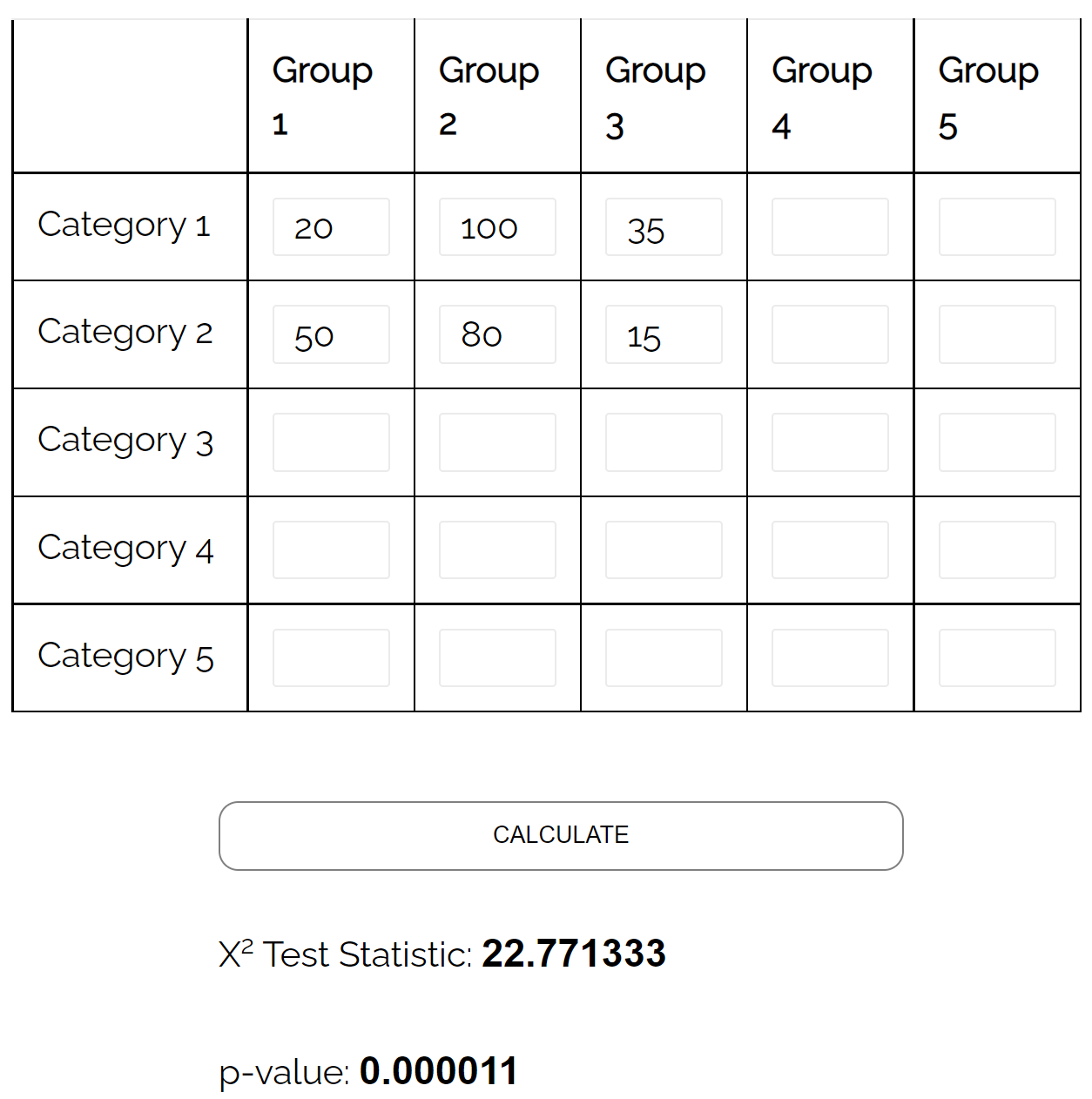
Omdat de p-waarde kleiner is dan 0,05, is er voldoende bewijs om te zeggen dat er een verband bestaat tussen burgerlijke staat en opleidingsniveau.
Aanvullende bronnen
De volgende tutorials bieden een inleiding tot de verschillende soorten Chi-kwadraattoetsen:
In de volgende tutorials wordt het verschil uitgelegd tussen Chi-kwadraattoetsen en andere statistische toetsen: