Hoe voer je een chow-test uit in r

Een Chow-test wordt gebruikt om te testen of de coëfficiënten van twee verschillende regressiemodellen op verschillende datasets gelijk zijn.

Deze test wordt doorgaans gebruikt op het gebied van de econometrie met tijdreeksgegevens om te bepalen of er op een bepaald moment een structurele breuk in de gegevens is.

Deze tutorial biedt een stapsgewijs voorbeeld van hoe u een Chow-test uitvoert in R.

Stap 1: Creëer de gegevens

Eerst zullen we valse gegevens creëren:

 #create data
data <- data.frame(x = c(1, 1, 2, 3, 4, 4, 5, 5, 6, 7, 7, 8, 8, 9, 10, 10,
                         11, 12, 12, 13, 14, 15, 15, 16, 17, 18, 18, 19, 20, 20),
                   y = c(3, 5, 6, 10, 13, 15, 17, 14, 20, 23, 25, 27, 30, 30, 31,
                         33, 32, 32, 30, 32, 34, 34, 37, 35, 34, 36, 34, 37, 38, 36))

#view first six rows of data
head(data)

  xy
1 1 3
2 1 5
3 2 6
4 3 10
5 4 13
6 4 15

Stap 2: Visualiseer de gegevens

Vervolgens maken we een eenvoudig spreidingsdiagram om de gegevens te visualiseren:

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(data, aes (x = x, y = y)) +
    geom_point(col=' steelblue ', size= 3 )

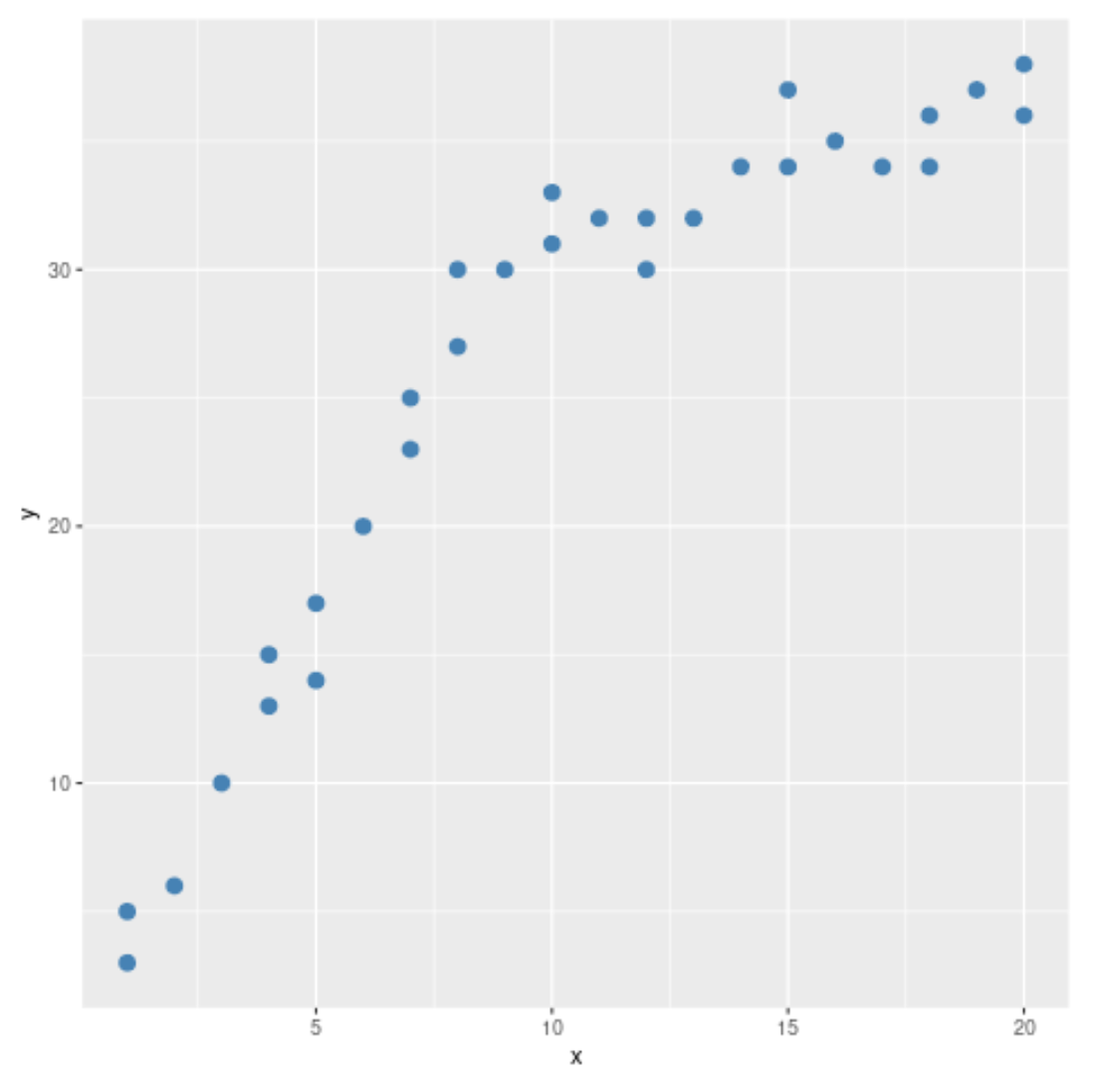
Uit het spreidingsdiagram kunnen we zien dat het patroon in de gegevens lijkt te veranderen bij x = 10. We kunnen dus de Chow-test uitvoeren om te bepalen of er een structureel breekpunt in de gegevens is bij x = 10.

Stap 3: Voer de Chow-test uit

We kunnen de sctest- functie uit het strucchange- pakket gebruiken om een Chow-test uit te voeren:

 #load strucchange package
library (strucchange)

#perform Chow test
sctest(data$y ~ data$x, type = " Chow ", point = 10 )

	Chow test

data: data$y ~ data$x
F = 110.14, p-value = 2.023e-13

Uit het testresultaat kunnen we zien:

• F-teststatistiek : 110,14
• p-waarde: <.0000

Omdat de p-waarde kleiner is dan 0,05, kunnen we de nulhypothese van de test verwerpen. Dit betekent dat we voldoende bewijs hebben om te zeggen dat er een structureel breekpunt in de gegevens aanwezig is.

Met andere woorden: twee regressielijnen kunnen het model effectiever in de gegevens passen dan één enkele regressielijn.