Een inleiding tot classificatie- en regressiebomen

Wanneer de relatie tussen een reeks voorspellende variabelen en een responsvariabele lineair is, kunnen methoden zoals meervoudige lineaire regressie nauwkeurige voorspellende modellen opleveren.

Wanneer de relatie tussen een reeks voorspellers en een respons echter zeer niet-lineair en complex is, kunnen niet-lineaire methoden beter presteren.

Een voorbeeld van een niet-lineaire methode zijn classificatie- en regressiebomen , vaak afgekort CART .

Zoals de naam al doet vermoeden, gebruiken CART-modellen een reeks voorspellende variabelen om beslissingsbomen te creëren die de waarde van een responsvariabele voorspellen.

Stel dat we bijvoorbeeld een dataset hebben met de voorspellende variabelen Gespeelde jaren en Gemiddelde homeruns en de responsvariabele Jaarsalaris voor honderden professionele honkbalspelers.

Zo zou een regressieboom er voor deze dataset uit kunnen zien:

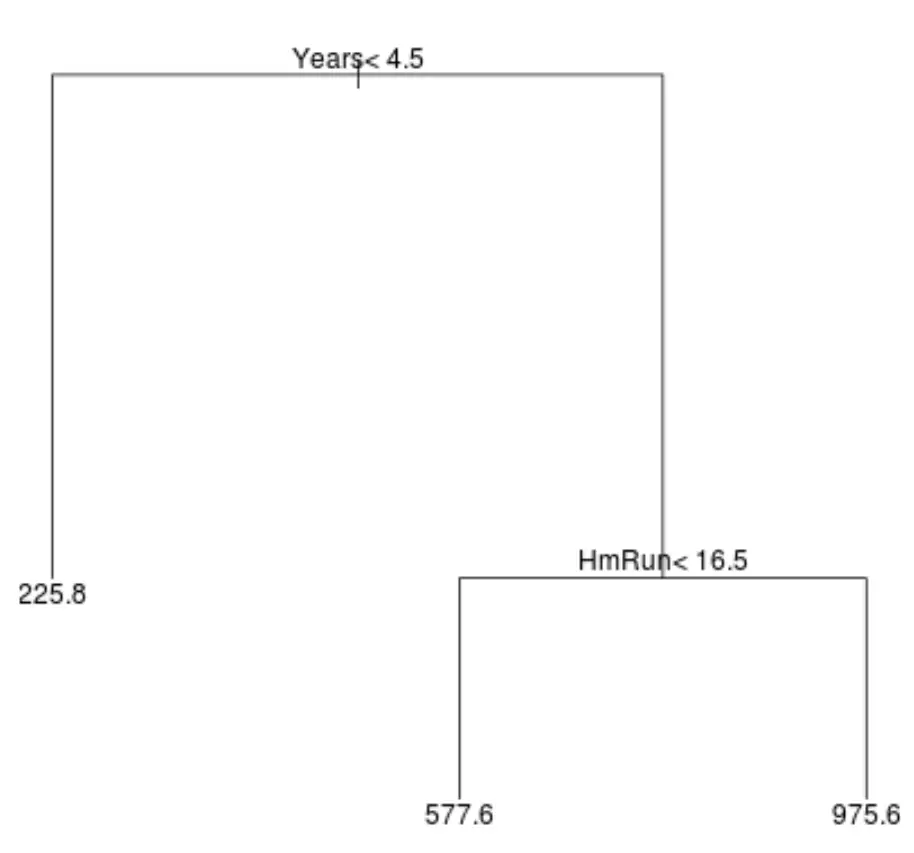
De manier om de boom te interpreteren is als volgt:

• Spelers die minder dan 4,5 jaar hebben gespeeld, hebben een verwacht salaris van $225,8k.
• Spelers die gemiddeld meer dan 4,5 jaar of langer en minder dan 16,5 homeruns hebben gespeeld, hebben een verwacht salaris van $577,6K.
• Spelers met 4,5 jaar of meer speelervaring en een gemiddelde van 16,5 homeruns of meer hebben een verwacht salaris van $975,6K.

De resultaten van dit model zouden intuïtief logisch moeten zijn: spelers met meer jaren ervaring en meer gemiddelde homeruns verdienen doorgaans hogere salarissen.

Dit model kunnen we vervolgens gebruiken om het salaris van een nieuwe speler te voorspellen.

Laten we bijvoorbeeld zeggen dat een bepaalde speler acht jaar heeft gespeeld en gemiddeld tien homeruns per jaar maakt. Volgens ons model voorspellen we dat deze speler een jaarsalaris heeft van $577,6k.

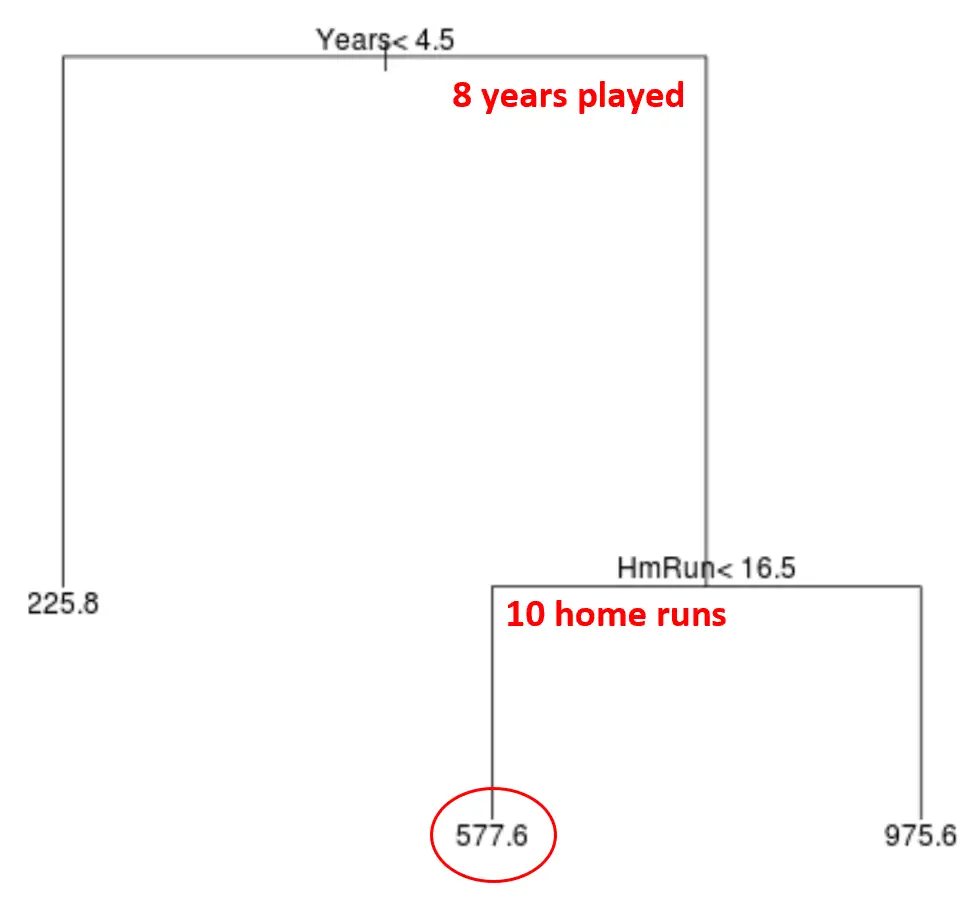
Enkele opmerkingen over de boom:

• De eerste voorspellende variabele bovenaan de boom is de belangrijkste, dat wil zeggen degene die de meeste invloed heeft op de voorspelling van de waarde van de responsvariabele. In dit geval voorspellen de gespeelde jaren het salaris beter dan het gemiddelde van de circuits .
• De gebieden onderaan de boom worden bladknopen genoemd. Deze specifieke boom heeft drie eindknooppunten.

Stappen om CART-modellen te maken

We kunnen de volgende stappen gebruiken om een CART-model voor een bepaalde dataset te maken:

Stap 1: Gebruik recursieve binaire splitsing om een grote boom op basis van de trainingsgegevens te laten groeien.

Ten eerste gebruiken we een hebzuchtig algoritme genaamd recursieve binaire splitsing om een regressieboom te laten groeien met behulp van de volgende methode:

• Beschouw alle voorspellende variabelen X _{1 ,} X ₂ , … , resterende standaardfout) als de laagste. .
  • Voor classificatiebomen kiezen we de voorspeller en het cutpoint zodanig dat de resulterende boom het laagste classificatiefoutenpercentage heeft.
• Herhaal dit proces en stop alleen wanneer elk eindknooppunt minder dan een bepaald minimumaantal waarnemingen heeft.

Dit algoritme is hebzuchtig omdat het bij elke stap van het boombouwproces bepaalt welke splitsing het beste kan worden gemaakt, alleen op basis van die stap, in plaats van naar de toekomst te kijken en een splitsing te kiezen die in een toekomstige fase tot een betere mondiale boom zal leiden.

Stap 2: Pas kostencomplexiteitssnoeien toe op de grote boom om een reeks van de beste bomen te verkrijgen, gebaseerd op α.

Zodra we de grote boom hebben laten groeien, moeten we hem snoeien met behulp van een methode die bekend staat als complex snoeien en die als volgt werkt:

• Zoek voor elke mogelijke boom met T-terminale knooppunten de boom die RSS + α|T| minimaliseert.
• Merk op dat wanneer we de waarde van α verhogen, bomen met meer eindknooppunten worden bestraft. Dit zorgt ervoor dat de boom niet te complex wordt.

Dit proces resulteert in een reeks van de beste bomen voor elke waarde van α.

Stap 3: Gebruik k-voudige kruisvalidatie om α te kiezen .

Zodra we de beste boom voor elke waarde van α hebben gevonden, kunnen we k-voudige kruisvalidatie toepassen om de waarde van α te kiezen die de testfout minimaliseert.

Stap 4: Kies de definitieve sjabloon.

Ten slotte kiezen we het uiteindelijke model dat overeenkomt met de gekozen waarde van α.

Voor- en nadelen van CART-modellen

CART-modellen bieden de volgende voordelen :

• Ze zijn gemakkelijk te interpreteren.
• Ze zijn gemakkelijk uit te leggen.
• Ze zijn gemakkelijk te visualiseren.
• Ze kunnen worden toegepast op zowel regressie- als classificatieproblemen .

CART-modellen hebben echter de volgende nadelen:

• Ze hebben doorgaans niet zoveel voorspellende nauwkeurigheid als andere niet-lineaire machine learning-algoritmen. Door veel beslissingsbomen te clusteren met methoden als bagging, boosting en willekeurige forests kan hun voorspellende nauwkeurigheid echter worden verbeterd.

Gerelateerd: Hoe classificatie- en regressiebomen in R te passen