Hoe classificatie- en regressiebomen in r passen

Wanneer de relatie tussen een reeks voorspellende variabelen en een responsvariabele lineair is, kunnen methoden zoals meervoudige lineaire regressie nauwkeurige voorspellende modellen opleveren.

Wanneer de relatie tussen een reeks voorspellers en een respons echter complexer is, kunnen niet-lineaire methoden vaak nauwkeurigere modellen opleveren.

Eén zo’n methode is classificatie- en regressiebomen (CART), waarbij een reeks voorspellende variabelen wordt gebruikt om beslissingsbomen te creëren die de waarde van een responsvariabele voorspellen.

Als de responsvariabele continu is, kunnen we regressiebomen bouwen en als de responsvariabele categorisch is, kunnen we classificatiebomen bouwen.

In deze tutorial wordt uitgelegd hoe u regressie- en classificatiebomen maakt in R.

Voorbeeld 1: Een regressieboom bouwen in R

Voor dit voorbeeld gebruiken we de Hitters- dataset uit het ISLR- pakket, die verschillende informatie bevat over 263 professionele honkbalspelers.

We zullen deze dataset gebruiken om een regressieboom te construeren die de voorspellende variabelen van homeruns en gespeelde jaren gebruikt om het salaris van een bepaalde speler te voorspellen.

Gebruik de volgende stappen om deze regressieboom te maken.

Stap 1: Laad de benodigde pakketten.

Eerst laden we de benodigde pakketten voor dit voorbeeld:

 library (ISLR) #contains Hitters dataset
library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

Stap 2: Bouw de initiële regressieboom.

Eerst zullen we een grote initiële regressieboom bouwen. We kunnen garanderen dat de boom groot is door een kleine waarde te gebruiken voor cp , wat staat voor „complexiteitsparameter“.

Dit betekent dat we verdere splitsingen op de regressieboom zullen uitvoeren zolang de totale R-kwadraat van het model toeneemt met ten minste de waarde gespecificeerd door cp.

We zullen dan de functie printcp() gebruiken om de modelresultaten af te drukken:

 #build the initial tree
tree <- rpart(Salary ~ Years + HmRun, data=Hitters, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] HmRun Years

Root node error: 53319113/263 = 202734

n=263 (59 observations deleted due to missingness)

           CP nsplit rel error xerror xstd
1 0.24674996 0 1.00000 1.00756 0.13890
2 0.10806932 1 0.75325 0.76438 0.12828
3 0.01865610 2 0.64518 0.70295 0.12769
4 0.01761100 3 0.62652 0.70339 0.12337
5 0.01747617 4 0.60891 0.70339 0.12337
6 0.01038188 5 0.59144 0.66629 0.11817
7 0.01038065 6 0.58106 0.65697 0.11687
8 0.00731045 8 0.56029 0.67177 0.11913
9 0.00714883 9 0.55298 0.67881 0.11960
10 0.00708618 10 0.54583 0.68034 0.11988
11 0.00516285 12 0.53166 0.68427 0.11997
12 0.00445345 13 0.52650 0.68994 0.11996
13 0.00406069 14 0.52205 0.68988 0.11940
14 0.00264728 15 0.51799 0.68874 0.11916
15 0.00196586 16 0.51534 0.68638 0.12043
16 0.00016686 17 0.51337 0.67577 0.11635
17 0.00010000 18 0.51321 0.67576 0.11615
n=263 (59 observations deleted due to missingness)

Stap 3: Snoei de boom.

Vervolgens zullen we de regressieboom snoeien om de optimale waarde te vinden die we kunnen gebruiken voor cp (de complexiteitsparameter) die tot de laagste testfout leidt.

Merk op dat de optimale waarde voor cp degene is die leidt tot de laagste x-fout in de vorige uitvoer, die de fout vertegenwoordigt op de waarnemingen uit de kruisvalidatiegegevens.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

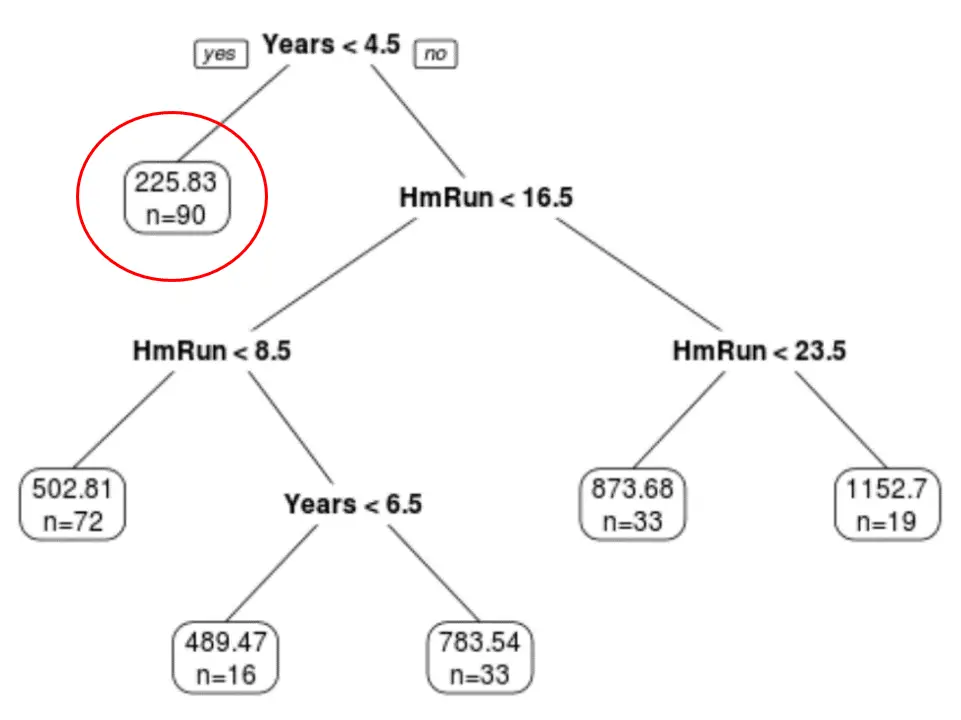
We kunnen zien dat de uiteindelijk gesnoeide boom zes eindknooppunten heeft. Elk bladknooppunt geeft het voorspelde salaris weer van de spelers in dat knooppunt, evenals het aantal observaties uit de oorspronkelijke dataset dat bij die rang hoort.

We kunnen bijvoorbeeld zien dat er in de originele dataset 90 spelers waren met minder dan 4,5 jaar ervaring en dat hun gemiddelde salaris $225,83K bedroeg.

Stap 4: Gebruik de boom om voorspellingen te doen.

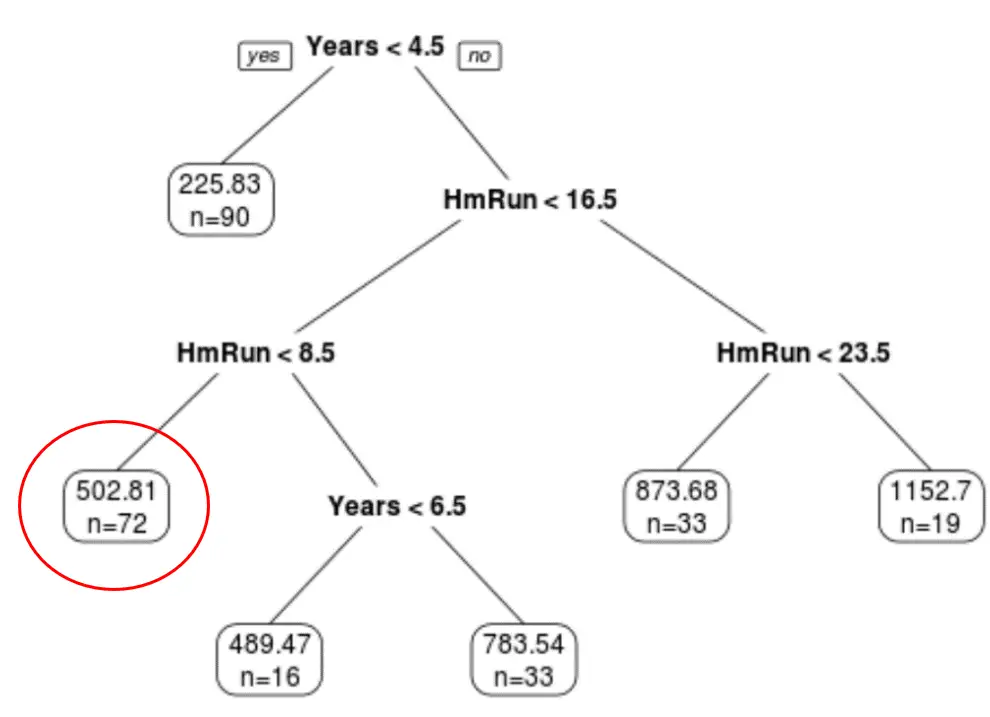
We kunnen de laatst gesnoeide boom gebruiken om het salaris van een bepaalde speler te voorspellen op basis van zijn jarenlange ervaring en gemiddelde homeruns.

Een speler met zeven jaar ervaring en gemiddeld vier homeruns heeft bijvoorbeeld een verwacht salaris van €502,81k .

We kunnen de voorspellen() functie in R gebruiken om dit te bevestigen:

 #define new player
new <- data.frame(Years=7, HmRun=4)

#use pruned tree to predict salary of this player
predict(pruned_tree, newdata=new)

502.8079

Voorbeeld 2: Een classificatieboom bouwen in R

Voor dit voorbeeld gebruiken we de ptitanic- dataset uit het pakket rpart.plot , die verschillende informatie bevat over de passagiers aan boord van de Titanic.

We zullen deze dataset gebruiken om een classificatieboom te maken die de voorspellende variabelen klasse , geslacht en leeftijd gebruikt om te voorspellen of een bepaalde passagier het heeft overleefd of niet.

Gebruik de volgende stappen om deze classificatieboom te maken.

Stap 1: Laad de benodigde pakketten.

Eerst laden we de benodigde pakketten voor dit voorbeeld:

 library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

Stap 2: Bouw de initiële classificatieboom.

Eerst zullen we een grote initiële classificatieboom bouwen. We kunnen garanderen dat de boom groot is door een kleine waarde te gebruiken voor cp , wat staat voor „complexiteitsparameter“.

Dit betekent dat we verdere splitsingen in de classificatieboom zullen uitvoeren zolang de algehele modelfit met ten minste de door cp gespecificeerde waarde toeneemt.

We zullen dan de functie printcp() gebruiken om de modelresultaten af te drukken:

 #build the initial tree
tree <- rpart(survived~pclass+sex+age, data=ptitanic, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] age pclass sex   

Root node error: 500/1309 = 0.38197

n=1309 

      CP nsplit rel error xerror xstd
1 0.4240 0 1.000 1.000 0.035158
2 0.0140 1 0.576 0.576 0.029976
3 0.0095 3 0.548 0.578 0.030013
4 0.0070 7 0.510 0.552 0.029517
5 0.0050 9 0.496 0.528 0.029035
6 0.0025 11 0.486 0.532 0.029117
7 0.0020 19 0.464 0.536 0.029198
8 0.0001 22 0.458 0.528 0.029035

Stap 3: Snoei de boom.

Vervolgens zullen we de regressieboom snoeien om de optimale waarde te vinden die we kunnen gebruiken voor cp (de complexiteitsparameter) die tot de laagste testfout leidt.

Merk op dat de optimale waarde voor cp degene is die leidt tot de laagste x-fout in de vorige uitvoer, die de fout vertegenwoordigt op de waarnemingen uit de kruisvalidatiegegevens.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

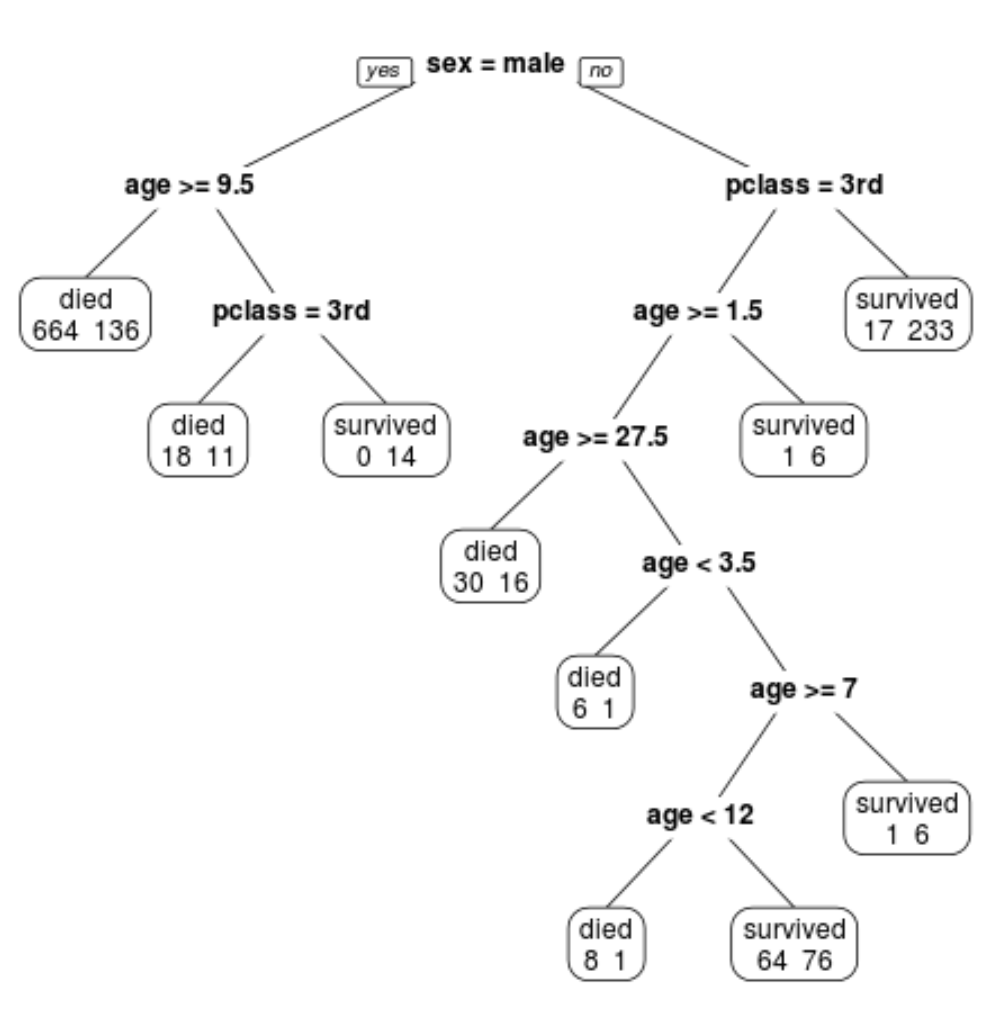
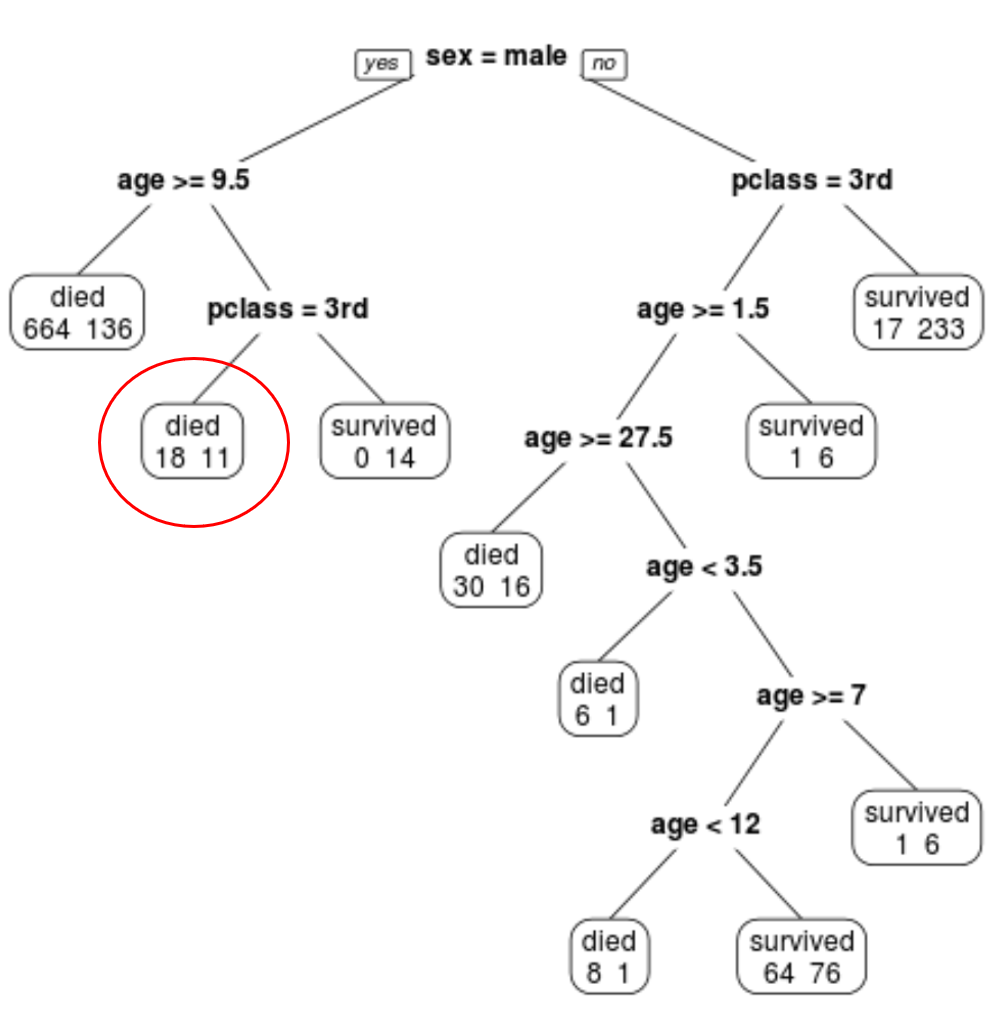
We kunnen zien dat de uiteindelijk gesnoeide boom 10 eindknooppunten heeft. Elk terminalknooppunt geeft het aantal omgekomen passagiers aan, evenals het aantal overlevenden.

In het meest linkse knooppunt zien we bijvoorbeeld dat 664 passagiers omkwamen en 136 overleefden.

Stap 4: Gebruik de boom om voorspellingen te doen.

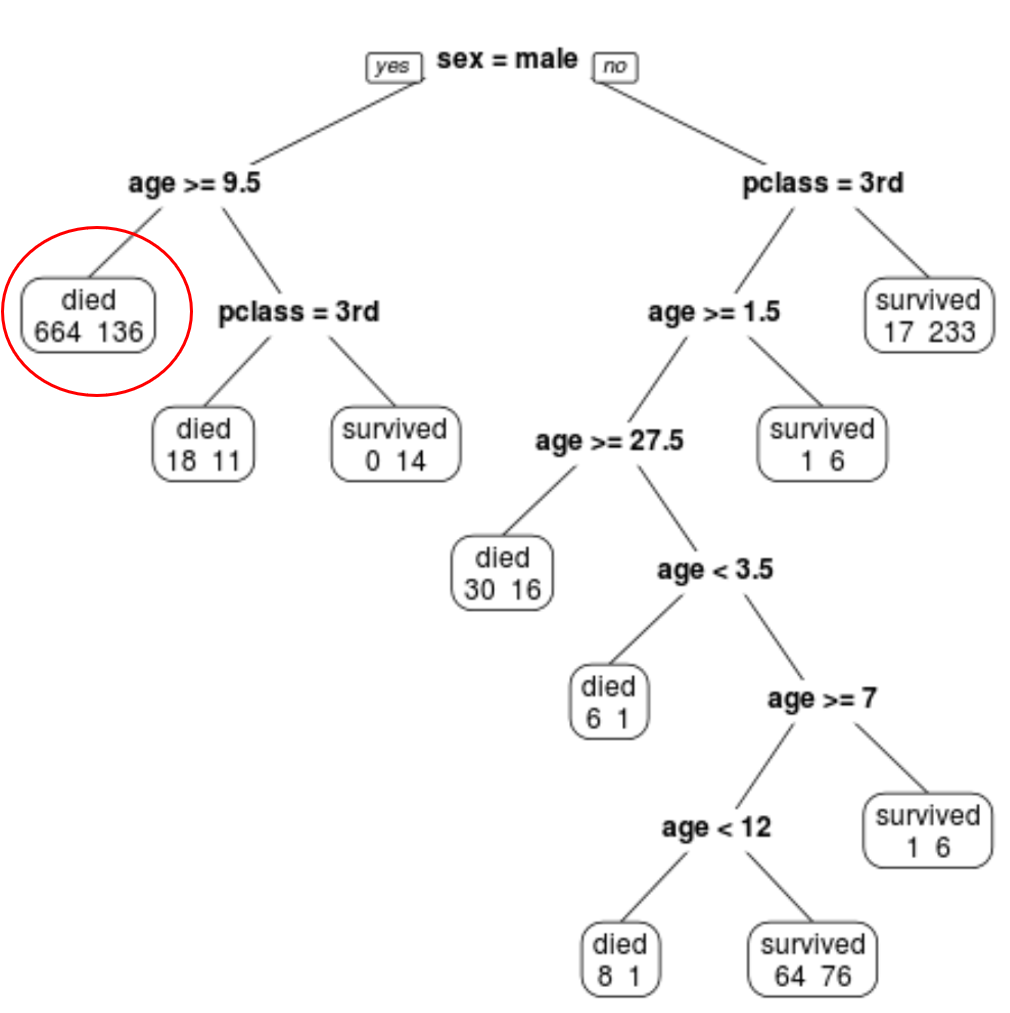
We kunnen de laatste gesnoeide boom gebruiken om de waarschijnlijkheid te voorspellen dat een bepaalde passagier zal overleven op basis van zijn klasse, leeftijd en geslacht.

Een mannelijke passagier van 8 jaar en in de 1e klas heeft bijvoorbeeld een overlevingskans van 11/29 = 37,9%.

De volledige R-code die in deze voorbeelden wordt gebruikt, vindt u hier .