Wat is de q-test van cochran? (definitie & #038; voorbeeld)

Cochran’s Q-test is een statistische test die wordt gebruikt om te bepalen of het aandeel „successen“ gelijk is in drie of meer groepen waarin dezelfde individuen in elke groep voorkomen.

We kunnen bijvoorbeeld de Q-test van Cochran gebruiken om te bepalen of het aandeel studenten dat slaagt voor een toets gelijk is bij gebruik van drie verschillende studietechnieken.

Stappen om de Q-test van Cochran uit te voeren

De Q-test van Cochran gebruikt de volgende nul- en alternatieve hypothesen:

Nulhypothese (H ₀ ): Het aandeel “successen” is in alle groepen hetzelfde

Alternatieve hypothese ( _HA ): Het aandeel “successen” is in ten minste één van de groepen verschillend

De teststatistiek wordt als volgt berekend:

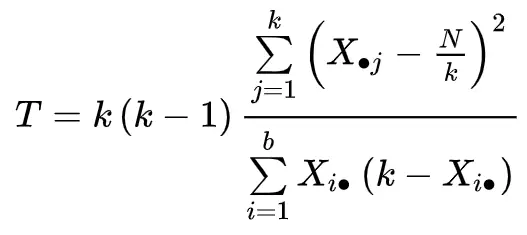
Goud:

• k: Het aantal behandelingen (of “groepen”)
• Xj: het totaal van de kolom voor de ^jde behandeling
• b: Het aantal blokken
• Xi. : Het totaal van de regel voor het ^i- de blok
• N: Het eindtotaal

De T- toetsstatistiek volgt een Chi-kwadraatverdeling met k-1 vrijheidsgraden.

Als de p-waarde die verband houdt met de teststatistiek onder een bepaald significantieniveau ligt (zoals α = 0,05), kunnen we de nulhypothese verwerpen en concluderen dat we voldoende bewijs hebben om te zeggen dat het aandeel ‘successen’ verschillend is in tenminste één van de groepen.

Voorbeeld: Cochran’s Q-test

Stel dat een onderzoeker wil weten of drie verschillende studietechnieken leiden tot verschillende percentages succespercentages onder studenten.

Om dit te testen werft ze twintig studenten die elk een examen van gelijke moeilijkheidsgraad afleggen met behulp van drie verschillende studietechnieken. De resultaten worden hieronder weergegeven:

Om de Q-test van Cochran uit te voeren, kunnen we statistische software gebruiken, omdat het lastig kan zijn om deze handmatig uit te voeren.

Hier is de code die we kunnen gebruiken om deze dataset te maken en de Q-test van Cochran uit te voeren in de statistische programmeertaal R:

 #load DescTools package
library (DescTools)

#create dataset
df <- data.frame(student= rep (1:20, each = 3 ),
                 technique= rep (c('A', 'B', 'C'), times= 20 ),
                 outcome=c(1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1,
                           1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1,
                           1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1,
                           1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1))

#perform Cochran's Q test
CochranQTest(outcome ~ technique| student, data=df)

	Cochran's Q test

data: outcome and technique and student
Q = 0.33333, df = 2, p-value = 0.8465

Uit het testresultaat kunnen we het volgende opmaken:

• De teststatistiek is 0,333
• De overeenkomstige p-waarde is 0,8465

Omdat deze p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen.

Dit betekent dat we niet genoeg bewijs hebben om te zeggen dat de door studenten gebruikte studietechniek tot verschillende verhoudingen van succespercentages leidt.