Controlelimieten

Von Dr.benjamin anderson August 2, 2023 Kwaliteitsmanagement Keine Kommentare

In dit artikel wordt uitgelegd wat een controlelimiet is en wat de verschillende controlelimieten van een controlediagram zijn. Ook ziet u hoe controlegrenzen worden berekend en een uitgewerkt voorbeeld waarin de controlegrenzen van een proces worden bepaald.

Wat zijn controlelimieten?

Controlelimieten zijn de horizontale lijnen op een controlediagram die worden gebruikt om te bepalen of een proces gecontroleerd wordt of niet.

Een controlediagram heeft twee controlelimieten: de bovenste en onderste controlelimieten, die respectievelijk het controlegebied erboven en eronder afbakenen.

Controlelimieten zijn dus waarden die worden gebruikt om het controlegebied van een proces aan te geven. Als de meting van een proces binnen de controlegrenzen valt, betekent dit dat het proces wordt gecontroleerd. Anders moet de machine of het proces worden gecontroleerd omdat er waarschijnlijk sprake is van een afwijking.

Soorten controlelimieten

De controlelimieten zijn:

Upper Control Limit (LCS) : dit is de lijn die de maximale waarde aangeeft die in het proces wordt geaccepteerd.
Lower Control Limit (LCI) : Dit is de lijn die de minimumwaarde aangeeft die in het proces wordt geaccepteerd.
Centrale controlelijn : Dit is de lijn die de gemiddelde waarde van de grafiek weergeeft. Hoe dichter de punten bij deze lijn liggen, hoe stabieler het proces.

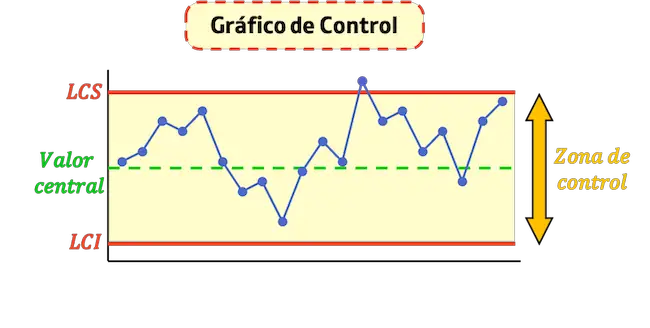
Hoe controlelimieten te berekenen

Momenteel worden de controlelimieten van een proces over het algemeen berekend door computersoftware waarmee het proces kan worden gecontroleerd. Het is echter ook belangrijk dat u weet hoe ze worden berekend, omdat u ze mogelijk handmatig moet opzoeken.

Het berekenen van de controlegrenzen van een controlediagram is afhankelijk van het type diagram dat u wilt maken, aangezien de waarden zullen veranderen afhankelijk van of het een controlediagram is voor het gemiddelde of voor het bereik.

Het gemiddelde controlediagram is een grafiek waarin de evolutie van het gemiddelde van een proces wordt geëvalueerd. Het gemiddelde van een reeks waarden wordt dus berekend met behulp van de volgende formule:

$\overline{X}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}$

Goud:

$x_i$

is het maatnummer i.
$n$

is het aantal uitgevoerde metingen.

We zullen de centrale waarde van het controlediagram voor het gemiddelde aanduiden als

$\overline{\overline{X}}$

, wat het gemiddelde is van de monsters en wordt berekend met de volgende uitdrukking:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}$

Goud:

$\overline{X}_j$

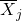
is het gemiddelde van monster j.
$m$

is het aantal genomen monsters.

➤ Zie: Berekening van het rekenkundig gemiddelde

De centrale waarde van het controlediagram voor de omvang is daarentegen het gemiddelde van de omvang van alle genomen monsters:

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}$

Goud:

$R_j$

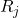
is het bereik van monster j.
$m$

is het aantal genomen monsters.

➤ Zie: Berekening van statistisch bereik

De formules voor het berekenen van de controlelimieten van een controlediagram zijn dus als volgt:

controle kaart

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}$

R-controlekaart

$\begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}$

Waar de waarden van de parameters A ₂ , D ₃ en D ₄ te vinden zijn in de volgende tabel:

Maat (nr.)	Op ₂	Dag ₃	_J4
2	1.880	0.000	3.267
3	1.023	0.000	2.575
4	0,729	0.000	2.282
5	0,577	0.000	2.115
6	0,483	0.000	2004
7	0,419	0,076	1.924
8	0,373	0,136	1.864
9	0,337	0,184	1.816
tien	0,308	0,223	1.777

Voorbeeld van het berekenen van controlelimieten

Een industrieel bedrijf wil de meting van de diameter van een cilinder controleren om te zien of het productieproces onder controle is. Neem hiervoor elke 15 minuten een monster van 5 cilinders en meet hun diameter. De volgende tabel toont de meetregistratie.

Om de controlelimieten te vinden, moeten we eerst het rekenkundige gemiddelde en het bereik van elke reeks metingen nemen:

voorbeelden van controlediagramberekeningen

Laten we nu het gemiddelde van de gemiddelden en de bereiken berekenen, wat de centrale waarden van het controlediagram zullen zijn voor respectievelijk het gemiddelde en het bereik:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}=4,8589$

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}=0,0227$

In dit geval bestaat elk monster uit 5 metingen, de coëfficiënten van de controlelimietformules zijn daarom als volgt:

$A_2=0,577$

$D_3=0$

$D_4=2,115$

We berekenen de bovenste en onderste controlegrenzen van het gemiddelde en uitgebreide controlediagram:

Controlediagram Controlelimieten

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}$

Controlegrenzen van R-controlekaart

$\begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}$

De oefencontrolekaarten zijn daarom als volgt:

voorbeeld van het berekenen van controlelimieten

In het eerste controlediagram kunnen we zien dat twee waarden kleiner zijn dan de onderste controlegrens. Bovendien is er in het tweede controlediagram ook een waarde boven de bovenste controlelimiet. Het proces wordt daarom niet gecontroleerd.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder

Wat zijn controlelimieten?

Soorten controlelimieten

Hoe controlelimieten te berekenen

Voorbeeld van het berekenen van controlelimieten

Über den Autor

Dr.benjamin anderson

Einen Kommentar hinzufügen