Controlekaart c

Von Dr.benjamin anderson August 1, 2023 Kwaliteitsmanagement Keine Kommentare

In dit artikel wordt uitgelegd wat een C-controlekaart is, wat de kenmerken ervan zijn en waarvoor deze wordt gebruikt. Daarnaast kun je stap voor stap zien hoe een C-controlediagram wordt gemaakt en een oefening wordt opgelost.

Wat is een C-controlediagram?

Een C-controlediagram , of eenvoudigweg een C-diagram , is een diagram dat per meeteenheid het aantal keren weergeeft dat een fenomeen voorkomt.

Controlediagram C wordt bijvoorbeeld gebruikt om te verifiëren dat het aantal productdefecten binnen de controlelimieten ligt.

Het is belangrijk op te merken dat controlediagram C niet het aantal defecte producten weergeeft, maar het aantal defecten dat elk product heeft. Om het aantal defecte producten te controleren, kunnen we een P- of NP-controlekaart gebruiken. Hieronder bekijken we de verschillen tussen alle soorten controlediagrammen.

De C-controlekaart heeft vele toepassingen. Zo kunt u bijvoorbeeld het aantal ontvangen klachten per dag, het aantal arbeidsongevallen per tijdseenheid, het aantal gebruikers per maand op een webpagina controleren, enz. .

Een van de kenmerken van het C-controlediagram is dat de steekproefgrootte constant moet zijn, dat wil zeggen dat alle geanalyseerde monsters dezelfde grootte moeten hebben.

Opgemerkt moet worden dat het wiskundige referentiemodel van het controlediagram C de Poisson-verdeling is. U kunt zien waaruit deze kansverdeling bestaat door hier te klikken:

➤ Zie: Wat is de Poisson-verdeling?

Hoe u een C-controlediagram maakt

De stappen voor het maken van een C-controlediagram zijn als volgt:

Monstername : eerst moeten er verschillende monsters genomen worden om de evolutie van het te meten fenomeen te kunnen volgen. De monsters moeten even groot zijn en daarnaast wordt aanbevolen om minimaal 20 monsters te nemen.
Bepaal het aantal keren dat het fenomeen voorkomt per meeteenheid : voor elk monster wordt het aantal keren dat het te onderzoeken fenomeen herhaald wordt.
Bereken de gemiddelde waarde van de gebeurtenissen : uit de verzamelde gegevens is het noodzakelijk om het gemiddelde te berekenen van de keren dat het fenomeen voorkomt per meeteenheid.

$\overline{c}=\cfrac{\text{N\'umero de veces que ocurre el fen\'omeno}}{\text{N\'umero de muestras}}$

Bereken controlelimieten voor Grafiek C – De controlelimieten voor Grafiek C moeten vervolgens worden berekend met behulp van de volgende formules:

$\displaystyle LCS=\overline{c}+3\sqrt{\overline{c}}$

$\displaystyle LCI=\overline{c}-3\sqrt{\overline{c}}$

Goud

$LCS$

$LCI$

zijn respectievelijk de bovenste en onderste controlelimieten en

$\overline{c}$

is de gemiddelde waarde van gebeurtenissen.

Waarden in een grafiek weergeven – De verzamelde waarden moeten nu met de berekende controlelimieten in een grafiek worden uitgezet.
Analyseer controlediagram C : uiteindelijk hoeft u alleen nog maar te controleren of geen enkele waarde op de grafiek buiten de controlegrenzen valt en dus of het proces onder controle is. Anders moet er actie worden ondernomen om het proces te corrigeren.

Voorbeeld van controlediagram C

Om u te laten zien hoe een C-controlediagram tot stand komt, is hier een voorbeeld stap voor stap uitgewerkt.

Een industrieel bedrijf wil het aantal defecten per product onder controle houden. Om dit te doen, neemt u 20 monsters van elk 3 producten en telt u het aantal waargenomen defecten per monster. U kunt de verzamelde gegevens in de onderstaande tabel bekijken. Analyseer het productieproces met behulp van een controlediagram C.

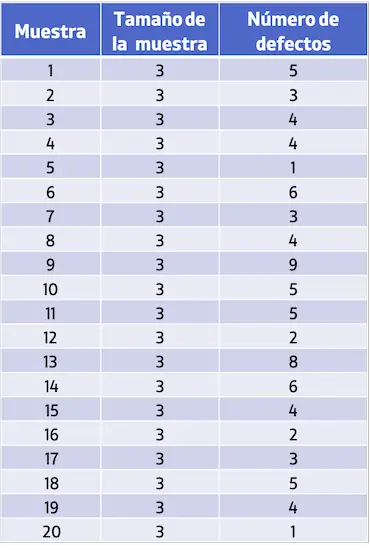
Om controlediagram C te produceren, is het noodzakelijk om de gemiddelde waarde van het aantal defecten per monster te berekenen:

$\overline{c}=\cfrac{\text{N\'umero de veces que ocurre el fen\'omeno}}{\text{N\'umero de muestras}}=\cfrac{84}{20}=4,2$

Laten we nu de controlelimieten van het C-diagram berekenen door de formules toe te passen die we hierboven hebben gezien:

$\displaystyle LCS=\overline{c}+3\sqrt{\overline{c}}=4,2+3\sqrt{4,2}=10,35$

$\displaystyle LCI=\overline{c}-3\sqrt{\overline{c}}=4,2-3\sqrt{4,2}=-1,95$

Het heeft geen zin dat een inspectielimiet negatief is, omdat onderdelen met een negatief aantal defecten niet kunnen worden vervaardigd. Daarom stellen we de onderste controlelimiet op 0.

Ten slotte plotten we alle waarden in een grafiek om het controlediagram C te verkrijgen:

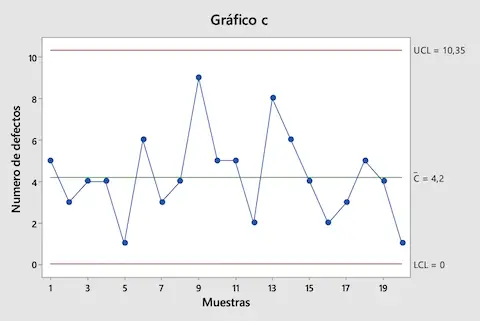
Zoals je kunt zien in grafiek C liggen alle waarden tussen de controlegrenzen, dus we concluderen dat het productieproces onder controle is.

Andere soorten controlediagrammen

Controlediagram C is een controlediagram voor attributen. Houd er echter rekening mee dat er verschillende soorten controlediagrammen zijn:

P-controlekaart : het aandeel producten met gebreken wordt gecontroleerd.
NP-controlekaart : het aantal defecte producten wordt gecontroleerd.
Controlediagram U : Het aantal defecten wordt gecontroleerd zoals in diagram C, maar de steekproefomvang kan variëren.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder