Hoe te converteren tussen z-scores en percentielen in excel

Een z-score vertelt ons hoeveel standaarddeviaties een bepaalde waarde afwijkt van het gemiddelde van een dataset.

Een percentiel vertelt ons welk percentage waarnemingen onder een bepaalde waarde in een dataset valt.

We willen vaak converteren tussen z-scores en percentielen, afhankelijk van het type vraag dat we proberen te beantwoorden. Gelukkig heeft Excel twee ingebouwde functies die het converteren tussen de twee eenvoudig maken.

Hoe Z-scores naar percentielen in Excel te converteren

We kunnen de volgende ingebouwde Excel-functie gebruiken om de az-score naar een percentiel te converteren:

=NORM.SD.VERD(z, cumulatief)

Goud:

• z = z-score van een bepaalde gegevenswaarde
• cumulatief = WAAR retourneert de cumulatieve verdelingsfunctie; FALSE retourneert de kansverdelingsfunctie. We zullen TRUE gebruiken om percentielen te berekenen.

U kunt als volgt bijvoorbeeld een z-score van 1,78 omzetten in een percentiel:

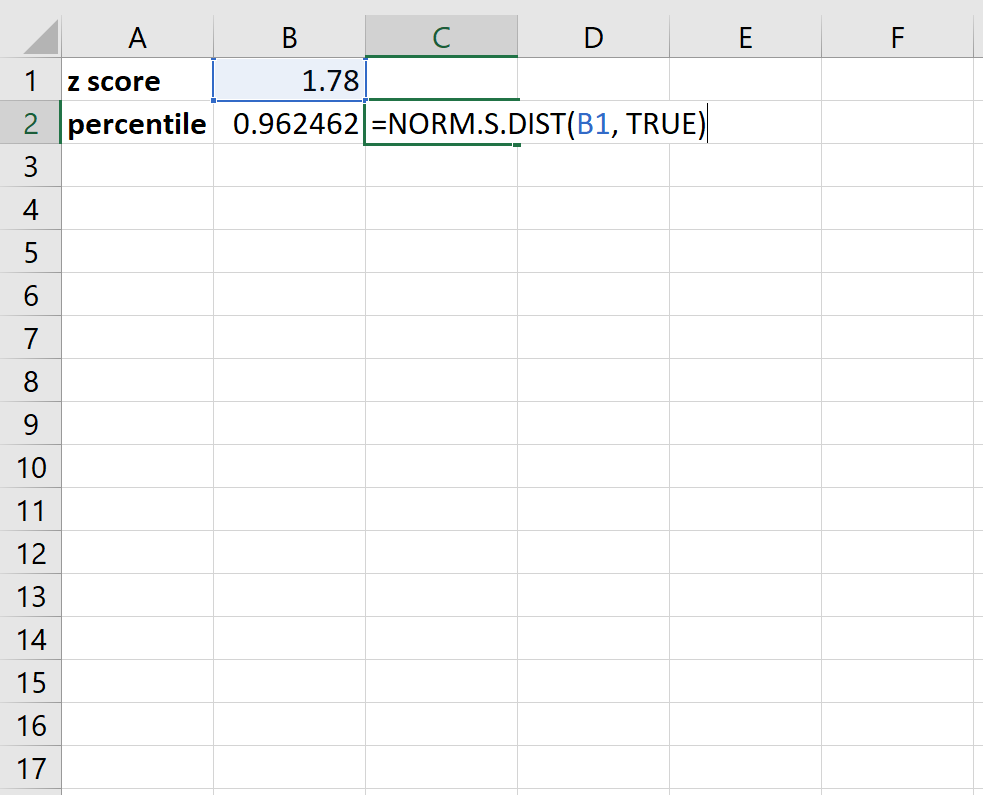
Het blijkt dat een z-score van 1,78 overeenkomt met een percentiel van ongeveer 96,2 . In gewoon Engels betekent dit dat een datawaarde met een z-score van 1,78 groter is dan ongeveer 96,2% van alle andere datawaarden in de dataset.

Hoe percentielen naar Z-scores in Excel te converteren

We kunnen de volgende ingebouwde Excel-functie gebruiken om een percentiel naar een z-score te converteren:

=NORM.S.INV(waarschijnlijkheid)

Goud:

• waarschijnlijkheid = het percentiel dat u wilt converteren.

U kunt als volgt bijvoorbeeld een percentiel van 0,85 omzetten in een z-score:

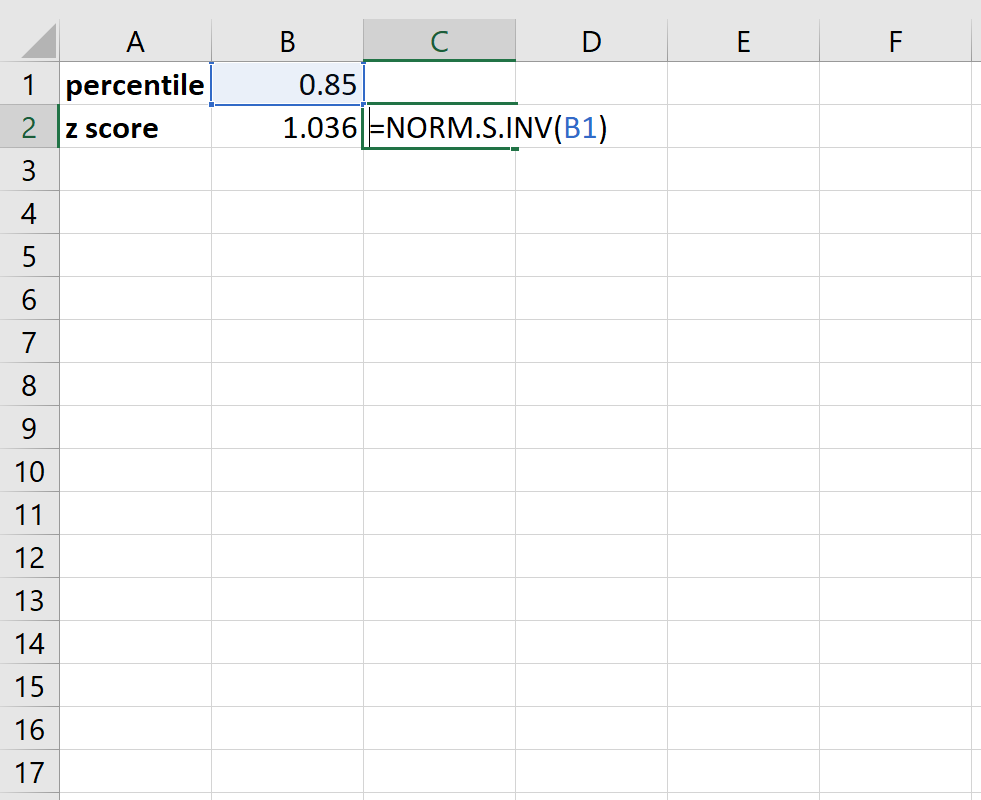
Het blijkt dat een percentiel van 0,85 overeenkomt met een z-score van ongeveer 1,036 . In gewoon Engels betekent dit dat een gegevenswaarde op het 85e percentiel in een gegevensset een z-score van 1,036 heeft.

De relatie tussen percentielen en Z-scores

Z-scores kunnen elke waarde aannemen tussen negatief oneindig en oneindig. Percentielen kunnen echter alleen waarden tussen 0 en 100 aannemen.

Een z-score van 0 komt overeen met een percentiel van precies 0,50. Elke z-score groter dan 0 komt dus overeen met een percentiel groter dan 0,50 en elke z-score kleiner dan 0 komt overeen met een percentiel kleiner dan 0,50.

Afhankelijk van het type vraag dat u probeert te beantwoorden, kan het nuttiger zijn om de z-score of het percentiel te kennen.

Stel bijvoorbeeld dat Jessica 90% haalt voor een bepaald examen. Dit lijkt misschien een hoge score, maar wat als het examen heel gemakkelijk was en zijn hele klas het goed deed? Om te bepalen hoe goed zijn cijfer is vergeleken met alle andere cijfers in de klas, kunnen we zowel de z-score als het percentiel van zijn examencijfer berekenen.

Als haar examenscore overeenkomt met een z-score van 1,23, betekent dit dat haar examenscore 1,23 standaardafwijkingen boven de gemiddelde examenscore lag. Deze z-score komt ook overeen met een percentiel van ongeveer 0,89, wat betekent dat ze hoger scoorde dan 89% van haar klasgenoten. Merk op hoe de z-score en het percentiel ons nuttige informatie geven over haar examenscore.