Hoe de correlatie tussen categorische variabelen te berekenen

We gebruiken vaak dePearson-correlatiecoëfficiënt om de correlatie tussen continue numerieke variabelen te berekenen.

We moeten echter een andere metriek gebruiken om de correlatie tussen categorische variabelen te berekenen, dat wil zeggen variabelen die namen of labels aannemen zoals:

• Burgerlijke staat (alleenstaand, getrouwd, gescheiden)
• Rookstatus (roker, niet-roker)
• Oogkleur (blauw, bruin, groen)

Er zijn drie veelgebruikte maatstaven om de correlatie tussen categorische variabelen te berekenen:

1. Tetrachorische correlatie: gebruikt om de correlatie tussen binaire categorische variabelen te berekenen.

2. Polychorische correlatie: gebruikt om de correlatie tussen ordinale categorische variabelen te berekenen.

3. Cramer’s V: gebruikt om de correlatie tussen nominale categorische variabelen te berekenen.

De volgende paragrafen geven een voorbeeld van hoe u elk van deze drie metingen kunt berekenen.

Metriek 1: Tetrachorische correlatie

Tetrachorische correlatie wordt gebruikt om de correlatie tussen binaire categorische variabelen te berekenen. Houd er rekening mee dat binaire variabelen variabelen zijn die slechts één van de twee mogelijke waarden kunnen aannemen.

De tetrachorische correlatiewaarde varieert van -1 tot 1, waarbij -1 een sterke negatieve correlatie aangeeft, 0 geen correlatie aangeeft en 1 een sterke positieve correlatie aangeeft.

Stel dat we bijvoorbeeld willen weten of gender wel of niet geassocieerd is met de voorkeur voor een politieke partij. Daarom nemen we een eenvoudige willekeurige steekproef van 100 kiezers en vragen hen naar hun voorkeur voor een politieke partij.

De volgende tabel geeft de resultaten van het onderzoek weer:

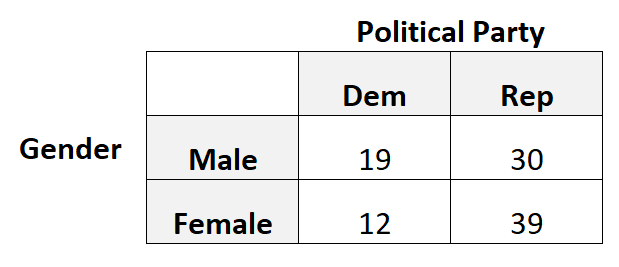
In dit scenario zouden we tetrachorische correlatie gebruiken omdat elke categorische variabele binair is, dat wil zeggen dat elke variabele slechts twee mogelijke waarden kan aannemen.

We kunnen de volgende code in R gebruiken om de tetrachorische correlatie tussen de twee variabelen te berekenen:

 library (psych)

#create 2x2 table
data = matrix(c(19, 12, 30, 39), nrow= 2 )

#view table
data

#calculate tetrachoric correlation
tetrachoric(data)

tetrachoric correlation 
[1] 0.27

De tetrachorische correlatie blijkt 0,27 te zijn. Deze waarde is vrij laag, wat aangeeft dat er een zwak (of al aanwezig) verband bestaat tussen geslacht en politieke partijvoorkeur.

Metriek 2: polychorische correlatie

Polychorische correlatie wordt gebruikt om de correlatie tussen ordinale categorische variabelen te berekenen. Bedenk dat ordinale variabelen variabelen zijn waarvan de mogelijke waarden een natuurlijke volgorde hebben.

De polychorische correlatiewaarde varieert van -1 tot 1, waarbij -1 een sterke negatieve correlatie aangeeft, 0 geen correlatie aangeeft en 1 een sterke positieve correlatie aangeeft.

Stel dat u bijvoorbeeld wilt weten of er bij twee verschillende filmbeoordelingsbureaus een hoge correlatie bestaat tussen hun filmbeoordelingen.

We vragen elk bureau om twintig verschillende films te beoordelen op een schaal van 1 tot 3, waarbij 1 ’slecht‘ betekent, 2 ’slecht‘ en 3 ‚goed‘.

De volgende tabel toont de resultaten:

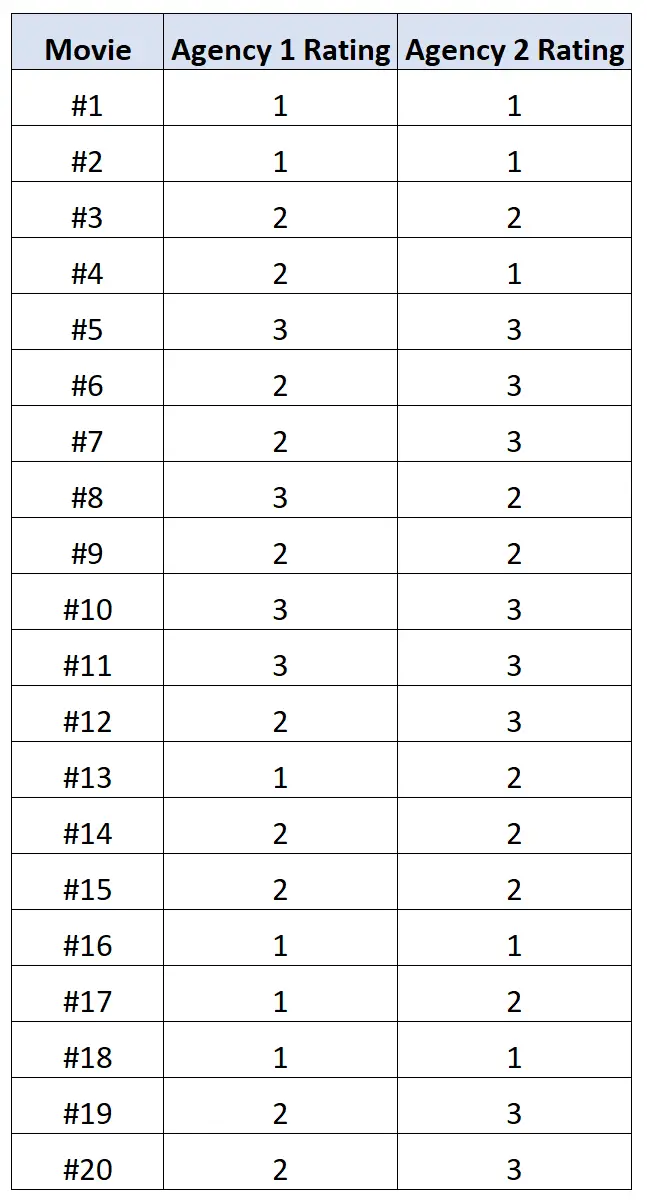
We kunnen de volgende code in R gebruiken om de polychorische correlatie tussen de beoordelingen van de twee bureaus te berekenen:

 library (polycor)

#define movie ratings
x <- c(1, 1, 2, 2, 3, 2, 2, 3, 2, 3, 3, 2, 1, 2, 2, 1, 1, 1, 2, 2)
y <- c(1, 1, 2, 1, 3, 3, 3, 2, 2, 3, 3, 3, 2, 2, 2, 1, 2, 1, 3, 3)

#calculate polychoric correlation between ratings
polychor(x, y)

[1] 0.7828328

De polychorische correlatie blijkt 0,78 te zijn. Deze waarde is vrij hoog, wat aangeeft dat er een sterk positief verband bestaat tussen de beoordelingen van elk bureau.

Metriek 3: Cramer’s V

Cramer’s V wordt gebruikt om de correlatie tussen nominale categorische variabelen te berekenen. Houd er rekening mee dat nominale variabelen variabelen zijn die categorielabels dragen, maar geen natuurlijke volgorde hebben.

De waarde van Cramer’s V varieert van 0 tot 1, waarbij 0 geen verband tussen de variabelen aangeeft en 1 een sterke associatie tussen de variabelen aangeeft.

Laten we bijvoorbeeld zeggen dat we willen weten of er een verband bestaat tussen oogkleur en geslacht. We ondervragen daarom 50 mensen en krijgen de volgende resultaten:

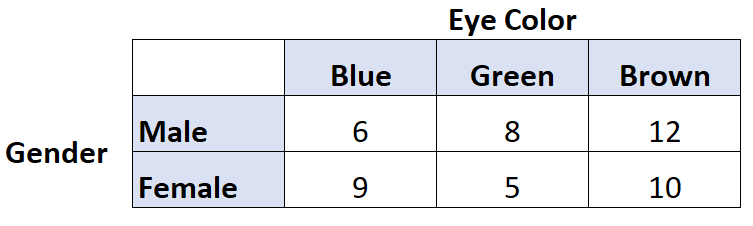
We kunnen de volgende code in R gebruiken om Cramer’s V voor deze twee variabelen te berekenen:

 library (rcompanion)

#create table
data = matrix(c(6, 9, 8, 5, 12, 10), nrow= 2 )

#view table
data

     [,1] [,2] [,3]
[1,] 6 8 12
[2,] 9 5 10

#calculate Cramer's V
cramerV(data)

Cramer V 
  0.1671

Cramer’s V blijkt 0,1671 te zijn. Deze waarde is vrij laag, wat aangeeft dat er een zwak verband bestaat tussen geslacht en oogkleur.

Aanvullende bronnen

Inleiding tot de Pearson-correlatiecoëfficiënt
Inleiding tot tetrachorische correlatie
Categorische of kwantitatieve variabelen: wat is het verschil?
Meetniveaus: nominaal, ordinaal, interval en ratio