Hoe u de correlatie tussen continue en categorische variabelen kunt berekenen

Wanneer we de correlatie tussen twee continue variabelen willen berekenen, gebruiken we doorgaans dePearson-correlatiecoëfficiënt .

Als we echter de correlatie tussen een continue variabele en eencategorische variabele willen berekenen, kunnen we de zogenaamde punt-biseriële correlatie gebruiken.

Punt-biseriële correlatie wordt gebruikt om de correlatie te berekenen tussen een binaire categorische variabele (een variabele die slechts twee waarden kan aannemen) en een continue variabele en heeft de volgende eigenschappen:

• De punt-biseriële correlatie kan variëren tussen -1 en 1.
• Voor elke groep die door de binaire variabele wordt gecreëerd, wordt aangenomen dat de continue variabele normaal verdeeld is met gelijke varianties.
• Voor elke groep die door de binaire variabele wordt gecreëerd, wordt aangenomen dat er geen extreme uitschieters zijn.

Het volgende voorbeeld laat zien hoe u in de praktijk een punt-biseriële correlatie kunt berekenen.

Voorbeeld: Berekening van een punt-biseriële correlatie

Stel dat een universiteitsprofessor wil vaststellen of er een verband bestaat tussen geslacht en de score op een bepaald kwalificerend examen.

Hij verzamelt de volgende gegevens over 12 jongens en 12 meisjes in zijn klas:

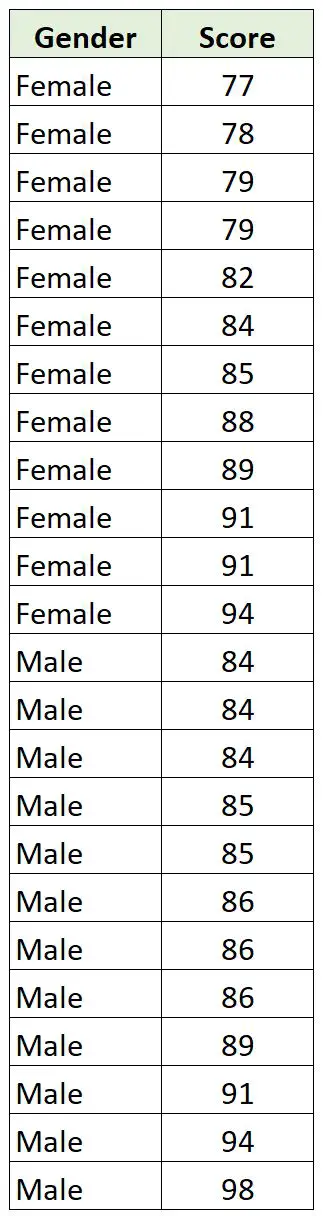
Omdat geslacht een categorische variabele is en de score een continue variabele, is het zinvol om een punt-biseriële correlatie tussen de twee variabelen te berekenen.

De professor kan elk statistisch programma (waaronder Excel, R, Python, SPSS, Stata) gebruiken om de punt-biseriële correlatie tussen de twee variabelen te berekenen.

De volgende code laat zien hoe de punt-biseriële correlatie in R wordt berekend, waarbij de waarde 0 wordt gebruikt om vrouwen weer te geven en 1 om mannen weer te geven voor de geslachtsvariabele:

 #define values for gender
gender <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
            1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)

#define values for score
score <- c(77, 78, 79, 79, 82, 84, 85, 88, 89, 91, 91, 94,
           84, 84, 84, 85, 85, 86, 86, 86, 89, 91, 94, 98)

#calculate point-biserial correlation
horn. test (gender, score)

	Pearson's product-moment correlation

data: gender and score
t = 1.3739, df = 22, p-value = 0.1833
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1379386 0.6147832
sample estimates:
      horn 
0.2810996

Uit het resultaat kunnen we zien dat de punt-biseriële correlatiecoëfficiënt 0,281 is en de overeenkomstige p-waarde 0,1833 .

Omdat de correlatiecoëfficiënt positief is, vertelt dit ons dat er een positieve correlatie bestaat tussen geslacht en score.

Omdat we mannen als 1 en vrouwen als 0 hebben gecodeerd, geeft dit aan dat de scores voor mannen doorgaans hoger zijn (dat wil zeggen: de scores nemen toe naarmate het geslacht ‚toeneemt‘). » van 0 tot 1).

Omdat de p-waarde echter niet kleiner is dan 0,05, is deze correlatiecoëfficiënt niet statistisch significant.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u de biseriële puntcorrelatie kunt berekenen met behulp van verschillende statistische software:

Hoe punt-biseriële correlatie in Excel te berekenen
Hoe de punt-biseriële correlatie in R te berekenen
Hoe punt-biseriële correlatie in Python te berekenen