Correlatie versus vereniging: wat is het verschil?

Twee termen die soms door elkaar worden gebruikt, zijn correlatie en associatie . Op het gebied van de statistiek hebben deze twee termen echter een enigszins verschillende betekenis.

Als we het woord correlatie gebruiken, hebben we het meestal over dePearson-correlatiecoëfficiënt . Het is een maatstaf voor de lineaire associatie tussen twee willekeurige variabelen X en Y. Het heeft een waarde tussen -1 en 1 waarbij:

• -1 geeft een perfect negatieve lineaire correlatie aan tussen twee variabelen
• 0 geeft aan dat er geen lineaire correlatie is tussen twee variabelen
• 1 geeft een perfect positieve lineaire correlatie aan tussen twee variabelen

Omgekeerd, als statistici het woord associatie gebruiken, kunnen ze het hebben over elke relatie tussen twee variabelen, zowel lineair als niet-lineair.

Om dit idee te illustreren, overweeg de volgende voorbeelden.

Visualiseren van correlatie en associatie met puntenwolken

We gebruiken twee woorden om de correlatie tussen twee willekeurige variabelen te beschrijven:

1 richting

• Positief: twee willekeurige variabelen hebben een positieve correlatie als Y de neiging heeft toe te nemen naarmate X toeneemt.
• Negatief: twee willekeurige variabelen hebben een negatieve correlatie als Y de neiging heeft af te nemen naarmate X toeneemt.

2. Kracht

• Laag: twee willekeurige variabelen hebben een lage correlatie als de punten in een spreidingsdiagram dun verspreid zijn.
• Sterk: Twee willekeurige variabelen hebben een sterke correlatie als de punten in een spreidingsdiagram dicht bij elkaar zijn gegroepeerd.

De volgende spreidingsdiagrammen illustreren voorbeelden van elk type correlatie:

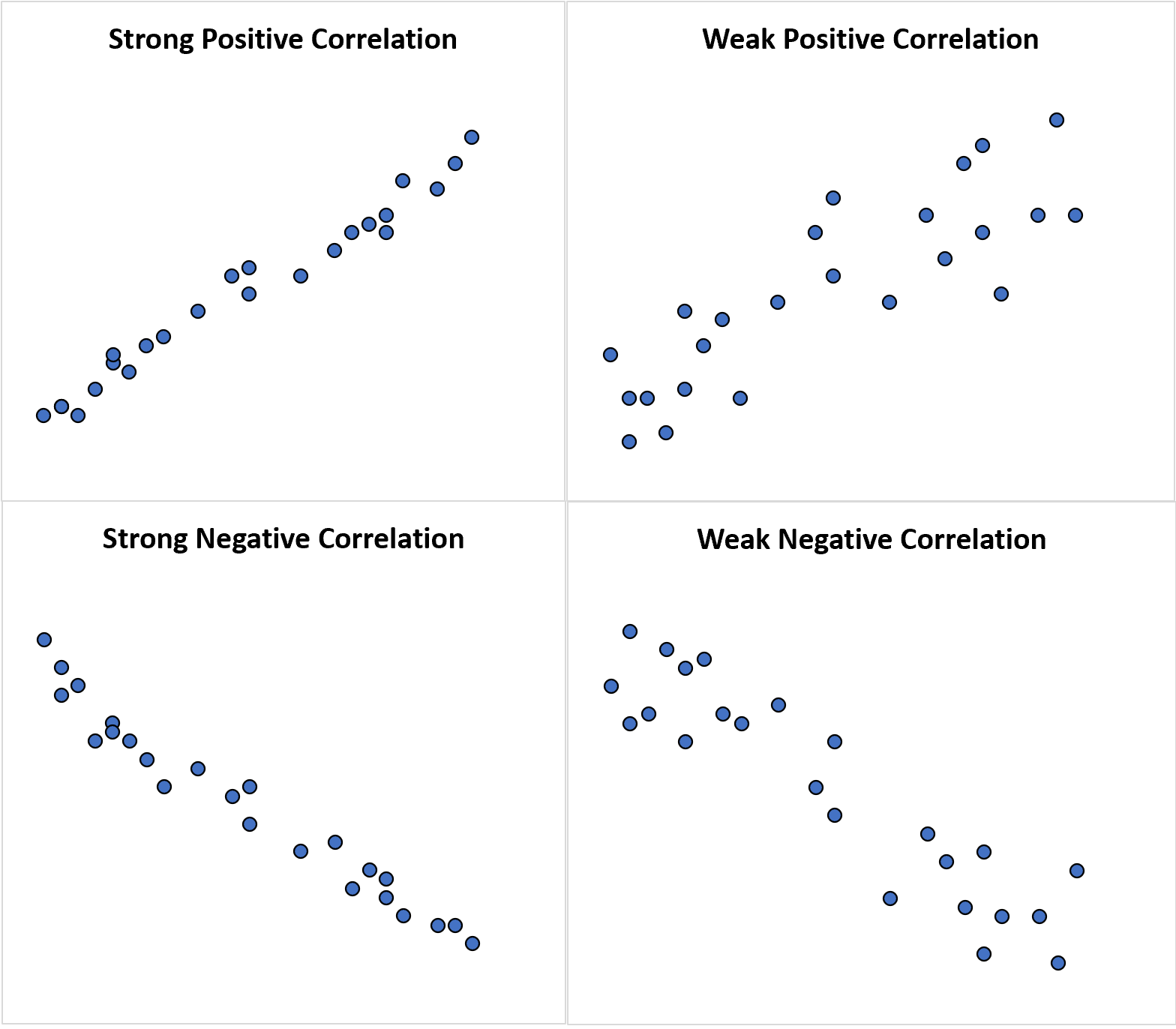
Vergeleken met correlatie kan het woord associatie ons vertellen of er wel of niet een verband bestaat tussen twee willekeurige variabelen: lineair of niet-lineair.

De volgende spreidingsdiagrammen illustreren enkele voorbeelden:

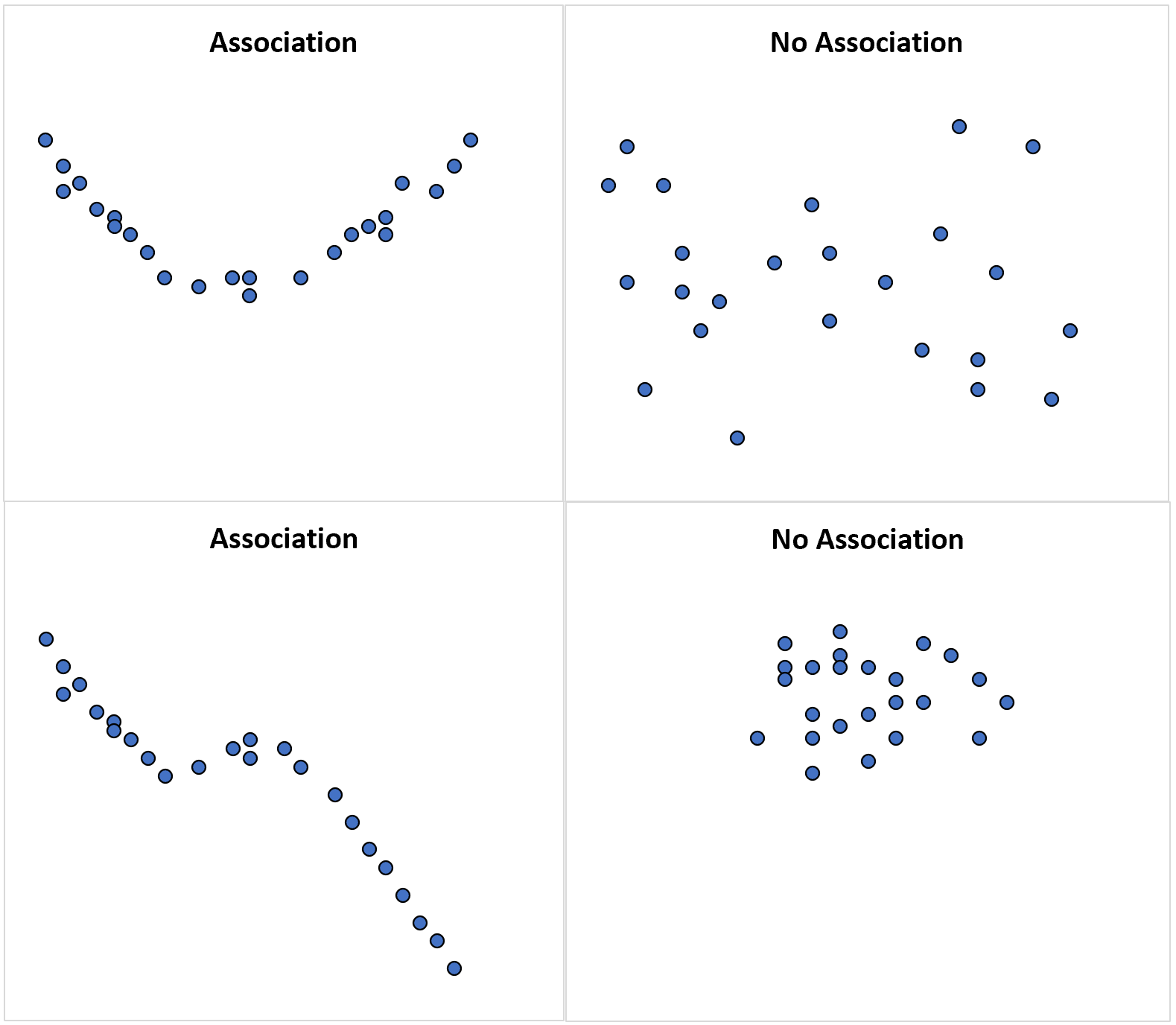
Het spreidingsdiagram in de linkerbovenhoek illustreert een kwadratische relatie tussen twee willekeurige variabelen, wat betekent dat er een verband bestaat tussen de twee variabelen, maar dat dit niet lineair is.

Als we de correlatie tussen de twee variabelen zouden berekenen, zou deze waarschijnlijk bijna nul zijn, omdat er geen lineair verband tussen beide bestaat.

Het eenvoudigweg weten dat de correlatie tussen de twee variabelen nul is, kan echter misleidend zijn, omdat hierdoor het feit wordt verborgen dat er in plaats daarvan een niet-lineair verband bestaat.

Correlatie versus vereniging: een samenvatting

De termen correlatie en associatie hebben de volgende overeenkomsten en verschillen:

Overeenkomsten:

• Beide termen worden gebruikt om te beschrijven of er al dan niet een verband bestaat tussen twee willekeurige variabelen.
• Beide termen kunnen spreidingsdiagrammen gebruiken om de relatie tussen twee willekeurige variabelen te analyseren.

Verschillen:

• Correlatie kan ons alleen vertellen of twee willekeurige variabelen een lineair verband hebben, terwijl associatie ons kan vertellen of twee willekeurige variabelen een lineair of niet-lineair verband hebben.
• Correlatie kwantificeert de relatie tussen twee willekeurige variabelen met behulp van een getal tussen -1 en 1, maar associatie gebruikt geen specifiek getal om een relatie te kwantificeren.

Aanvullende bronnen

Een inleiding tot de Pearson-correlatiecoëfficiënt
Een introductie tot puntenwolken
Correlatie versus regressie: wat is het verschil?