Correlatiecoëfficiënt binnen de klasse: definitie + voorbeeld

Een intraclass correlatiecoëfficiënt (ICC) wordt gebruikt om de betrouwbaarheid van scores te meten in onderzoeken waarbij er twee of meer beoordelaars zijn.

De waarde van een ICC kan variëren van 0 tot 1, waarbij 0 duidt op geen betrouwbaarheid onder de beoordelaars en 1 op perfecte betrouwbaarheid onder de beoordelaars.

Simpel gezegd wordt een ICC gebruikt om te bepalen of items (of onderwerpen) betrouwbaar kunnen worden beoordeeld door verschillende beoordelaars.

Er zijn verschillende versies van een ICC die kunnen worden berekend, afhankelijk van de volgende drie factoren:

• Model: willekeurige effecten in één richting, willekeurige effecten in twee richtingen of gemengde effecten in twee richtingen
• Type relatie: consistentie of absolute overeenstemming
• Eenheid: enkele beoordelaar of gemiddelde van beoordelaars

Hier volgt een korte beschrijving van de drie verschillende modellen :

1. Model met willekeurige effecten in één richting: Dit model gaat ervan uit dat elk onderwerp wordt geëvalueerd door een andere groep willekeurig geselecteerde beoordelaars. Met dit model worden beoordelaars beschouwd als de bron van willekeurige effecten. Dit model wordt in de praktijk zelden gebruikt, omdat voor elk onderwerp doorgaans dezelfde groep beoordelaars wordt gebruikt.

2. Tweerichtingsmodel met willekeurige effecten: Dit model gaat ervan uit dat een groep beoordelaars k willekeurig wordt geselecteerd uit een populatie en vervolgens wordt gebruikt om de proefpersonen te beoordelen. Met behulp van dit model worden beoordelaars en proefpersonen beschouwd als bronnen van willekeurige effecten. Dit model wordt vaak gebruikt als we onze resultaten willen generaliseren naar beoordelaars die vergelijkbaar zijn met de beoordelaars die in het onderzoek zijn gebruikt.

3. Tweerichtingsmodel met gemengde effecten: Dit model gaat er ook van uit dat een groep beoordelaars k willekeurig wordt geselecteerd uit een populatie en vervolgens wordt gebruikt om de proefpersonen te beoordelen. Dit model gaat er echter van uit dat de groep beoordelaars die we hebben gekozen de enige beoordelaars zijn die van belang zijn, wat betekent dat we onze resultaten niet willen generaliseren naar andere beoordelaars die mogelijk ook soortgelijke kenmerken delen als de beoordelaars die in het onderzoek zijn gebruikt.

Hier volgt een korte beschrijving van de twee verschillende soorten relaties die we mogelijk willen meten:

1. Consistentie: We zijn geïnteresseerd in systematische verschillen tussen de beoordelingen van juryleden (beoordeelden juryleden bijvoorbeeld vergelijkbare onderwerpen als laag en hoog?)

2. Absolute overeenstemming: we zijn geïnteresseerd in de absolute verschillen tussen de scores van de juryleden (wat is bijvoorbeeld het absolute verschil tussen de scores van jurylid A en jurylid B?)

Hier is een korte beschrijving van de twee verschillende eenheden die ons mogelijk interesseren:

1. Eén recensent: We willen de beoordelingen van slechts één recensent gebruiken als basis voor metingen.

2. Gemiddelde beoordelaar: We willen het gemiddelde van de scores van alle juryleden gebruiken als basis voor de meting.

Opmerking: als u de mate van overeenstemming wilt meten tussen twee beoordelaars die elk van de items over een dichotome uitkomst missen, moet u in plaats daarvan Cohen’s Kappa gebruiken.

Hoe de intraklasse-correlatiecoëfficiënt te interpreteren

Zo interpreteer je de waarde van een correlatiecoëfficiënt tussen klassen, volgens Koo & Li :

• Minder dan 0,50: slechte betrouwbaarheid
• Tussen 0,5 en 0,75: matige betrouwbaarheid
• Tussen 0,75 en 0,9: Goede betrouwbaarheid
• Groter dan 0,9: Uitstekende betrouwbaarheid

Het volgende voorbeeld laat zien hoe u in de praktijk een correlatiecoëfficiënt binnen een klasse kunt berekenen.

Voorbeeld: Berekening van de intraklasse-correlatiecoëfficiënt

Stel dat aan vier verschillende juryleden wordt gevraagd de kwaliteit van tien verschillende toelatingsexamens voor universiteiten te beoordelen. De resultaten worden hieronder weergegeven:

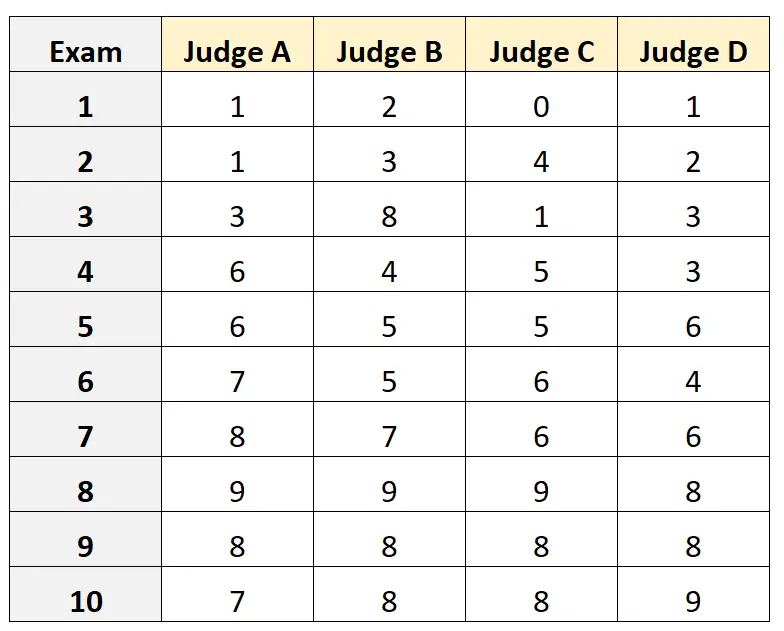
Stel dat de vier juryleden willekeurig werden geselecteerd uit een populatie van gekwalificeerde juryleden voor het toelatingsexamen en we de absolute overeenstemming tussen de juryleden wilden meten en we de scores vanuit het perspectief van slechts één beoordelaar als basis voor onze meting wilden gebruiken.

We kunnen de volgende code in R gebruiken om een tweerichtingsmodel voor willekeurige effecten te passen, waarbij absolute overeenstemming wordt gebruikt als de relatie tussen beoordelaars en de enkele eenheid wordt gebruikt als de eenheid van belang:

 #load the interrater reliability package
library (irr)

#define data
data <- data. frame (A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7),
                   B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8),
                   C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8),
                   D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9))

#calculate ICC
icc(data, model = " twoway ", type = " agreement ", unit = " single ")

   Model: twoway 
   Type: agreement 

   Subjects = 10 
     Failures = 4 
   ICC(A,1) = 0.782

 F-Test, H0: r0 = 0; H1: r0 > 0 
    F(9.30) = 15.3, p = 5.93e-09 

 95%-Confidence Interval for ICC Population Values:
  0.554 < ICC < 0.931

De intraclasscorrelatiecoëfficiënt (ICC) bleek 0,782 te zijn.

Op basis van de vuistregels voor de interpretatie van de ICC zouden we kunnen concluderen dat een ICC van 0,782 aangeeft dat examens door verschillende beoordelaars met “goede” betrouwbaarheid kunnen worden gescoord.

Aanvullende bronnen

De volgende tutorials bieden gedetailleerde uitleg over het berekenen van ICC in verschillende statistische software:

Hoe de intraclass-correlatiecoëfficiënt in Excel te berekenen
Hoe de intraklasse-correlatiecoëfficiënt in R te berekenen
Hoe de intraclass-correlatiecoëfficiënt in Python te berekenen