Correlatiematrix

In dit artikel ontdek je wat een correlatiematrix is, wat de formule ervan is en hoe je een correlatiematrix interpreteert. Daarnaast krijgt u een concreet voorbeeld te zien van de interpretatie van een correlatiematrix.

Wat is een correlatiematrix?

De correlatiematrix is een matrix die op positie i,j de correlatiecoëfficiënt bevat tussen de variabelen i en j .

Daarom is de correlatiematrix een vierkante matrix gevuld met enen op de hoofddiagonaal en bestaat het element van rij i en kolom j uit de waarde van de correlatiecoëfficiënt tussen variabele i en variabele j .

De formule voor de correlatiematrix is daarom als volgt:

Goud

is de correlatiecoëfficiënt tussen de variabelen

En

Om de correlatiematrix van een dataset te vinden, is het dus essentieel dat u weet hoe de correlatiecoëfficiënt wordt berekend. Mocht u het niet meer weten, dan leest u in de volgende link hoe u dit kunt doen met een online rekenmachine:

Een eigenschap van de correlatiecoëfficiënt is dat de volgorde van de variabelen er niet toe doet voor de berekening ervan, dat wil zeggen de correlatiecoëfficiënt

is gelijk aan

Daarom is de correlatiematrix symmetrisch.

Wil een correlatiematrix zinvol zijn, dan moet de statistische gegevensset meer dan twee variabelen bevatten. Anders zou het voldoende zijn om één enkele correlatiecoëfficiënt te bepalen en zou de correlatiematrix zinvol zijn.

Hoe maak je een correlatiematrix?

Laten we, gegeven de definitie van de correlatiematrix, eens kijken hoe dit type statistische matrix wordt gemaakt:

1. Bereken de correlatiecoëfficiënt van elk paar variabelen. Houd er rekening mee dat de volgorde van de variabelen het resultaat niet verandert, zodat het slechts één keer hoeft te worden berekend voor elk paar variabelen.
2. Maak een vierkante matrix met dezelfde dimensie als het aantal variabelen in de gegevensreeks. Deze matrix zal de correlatiematrix zijn.
3. Zet een 1 in elk element van de hoofddiagonaal van de correlatiematrix.
4. Zet de correlatiecoëfficiënt van variabelen i , j op de posities i , j en j , i .
5. Zodra de correlatiematrix is gemaakt, hoeft u alleen nog maar de waarden ervan te interpreteren.

Houd er rekening mee dat het simpelweg uitvoeren van de correlatiematrix niet voldoende is; u moet dan de waarden ervan interpreteren en begrijpen wat ze betekenen. In het volgende gedeelte wordt uitgelegd hoe u een correlatiematrix interpreteert.

Interpretatie van de correlatiematrix

Om de correlatiematrix correct te interpreteren, moet er rekening mee worden gehouden dat de waarde van de correlatiecoëfficiënt kan variëren van -1 tot +1:

• r=-1 : de twee variabelen hebben een perfecte negatieve correlatie, dus we kunnen een lijn tekenen met een negatieve helling waarin alle punten met elkaar verbonden zijn.
• -1<r<0 : de correlatie tussen de twee variabelen is negatief, dus als de ene variabele toeneemt, neemt de andere af. Hoe dichter de waarde bij -1 ligt, hoe negatiever de variabelen gerelateerd zijn.
• r=0 : de correlatie tussen de twee variabelen is erg zwak; de lineaire relatie daartussen is zelfs nul. Dit betekent niet dat de variabelen onafhankelijk zijn, aangezien ze een niet-lineair verband kunnen hebben.
• 0<r<1 : de correlatie tussen de twee variabelen is positief, hoe dichter de waarde bij +1 ligt, hoe sterker de relatie tussen de variabelen. In dit geval heeft de ene variabele de neiging zijn waarde te verhogen wanneer de andere ook toeneemt.
• r=1 : de twee variabelen hebben een perfecte positieve correlatie, dat wil zeggen, ze hebben een positieve lineaire relatie.

Om de correlatiematrix te interpreteren is het dus noodzakelijk om elke correlatiecoëfficiënt te interpreteren en de verschillende resultaten te vergelijken.

Zo kun je zien welke variabelen het meest met elkaar samenhangen, welke variabelen het belangrijkst zijn, welke variabelen vrijwel geen relatie met elkaar hebben, etc.

Voorbeeld van een correlatiematrix

Om volledig te begrijpen waaruit de correlatiematrix bestaat en hoe deze wordt geïnterpreteerd, zullen we in deze sectie een voorbeeld van een correlatiematrix analyseren:

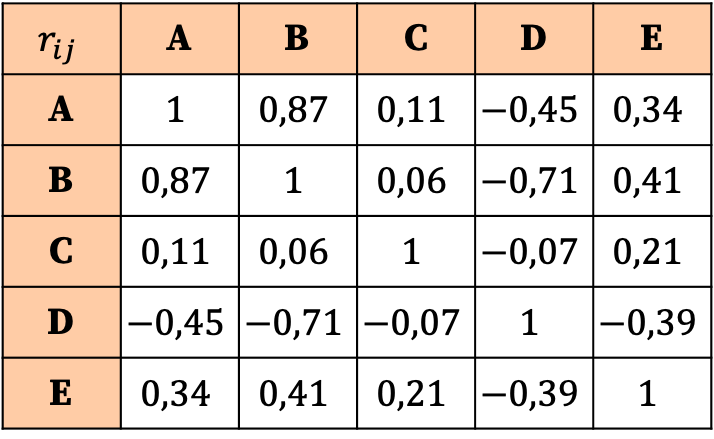
De interpretatie van de correlatiematrix is gebaseerd op de waarden van de coëfficiënten. We kunnen dus zien dat de sterkste correlatie de relatie is tussen variabele A en variabele B, aangezien de overeenkomstige coëfficiënt de grootste is (0,87).

Aan de andere kant heeft de variabele C vrijwel geen correlatie met welke variabele dan ook, aangezien al zijn coëfficiënten zeer dicht bij nul liggen en daarom zeer laag zijn. Om de analyse te vereenvoudigen zouden we dus zelfs kunnen overwegen om deze variabele uit het statistische onderzoek te verwijderen.

Op dezelfde manier zijn alle relaties van variabele D met andere variabelen negatief, wat betekent dat de correlatie tussen variabele D en andere variabelen omgekeerd is. Dit betekent niet dat de variabele moet worden geëlimineerd, maar wel dat de variabele D negatief gecorreleerd is.

Zoals u kunt zien, is de correlatiematrix erg handig voor het samenvatten van de gegevens en het maken van een algemene analyse van de relatie tussen verschillende variabelen in de dataset.