Een correlatietest uitvoeren in r (met voorbeelden)

Eén manier om de relatie tussen twee variabelen te kwantificeren is door de Pearson-correlatiecoëfficiënt te gebruiken, een maatstaf voor de lineaire associatie tussen twee variabelen .

Er is altijd een waarde tussen -1 en 1 nodig, waarbij:

• -1 geeft een perfect negatieve lineaire correlatie aan tussen twee variabelen
• 0 geeft aan dat er geen lineaire correlatie is tussen twee variabelen
• 1 geeft een perfect positieve lineaire correlatie aan tussen twee variabelen

Om te bepalen of een correlatiecoëfficiënt statistisch significant is, kun je de bijbehorende t-score en p-waarde berekenen.

De formule voor het berekenen van de t-score van een correlatiecoëfficiënt (r) is:

t = r * √ n-2 / √ 1-r ²

De p-waarde wordt berekend als de overeenkomstige tweezijdige p-waarde voor de t-verdeling met n-2 vrijheidsgraden.

Voorbeeld: correlatietest in R

Om te bepalen of de correlatiecoëfficiënt tussen twee variabelen statistisch significant is, kunt u een correlatietest uitvoeren in R met behulp van de volgende syntaxis:

cor.test(x, y, methode=c(“pearson”, “kendall”, “spearman”))

Goud:

• x, y: digitale datavectoren.
• methode: Methode die wordt gebruikt om de correlatie tussen twee vectoren te berekenen. De standaardinstelling is “Pearson”.

Stel bijvoorbeeld dat we de volgende twee vectoren in R hebben:

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

Voordat we een correlatietest tussen de twee variabelen uitvoeren, kunnen we een snelle spreidingsdiagram maken om hun relatie te visualiseren:

 #create scatterplot
plot(x, y, pch= 16 )

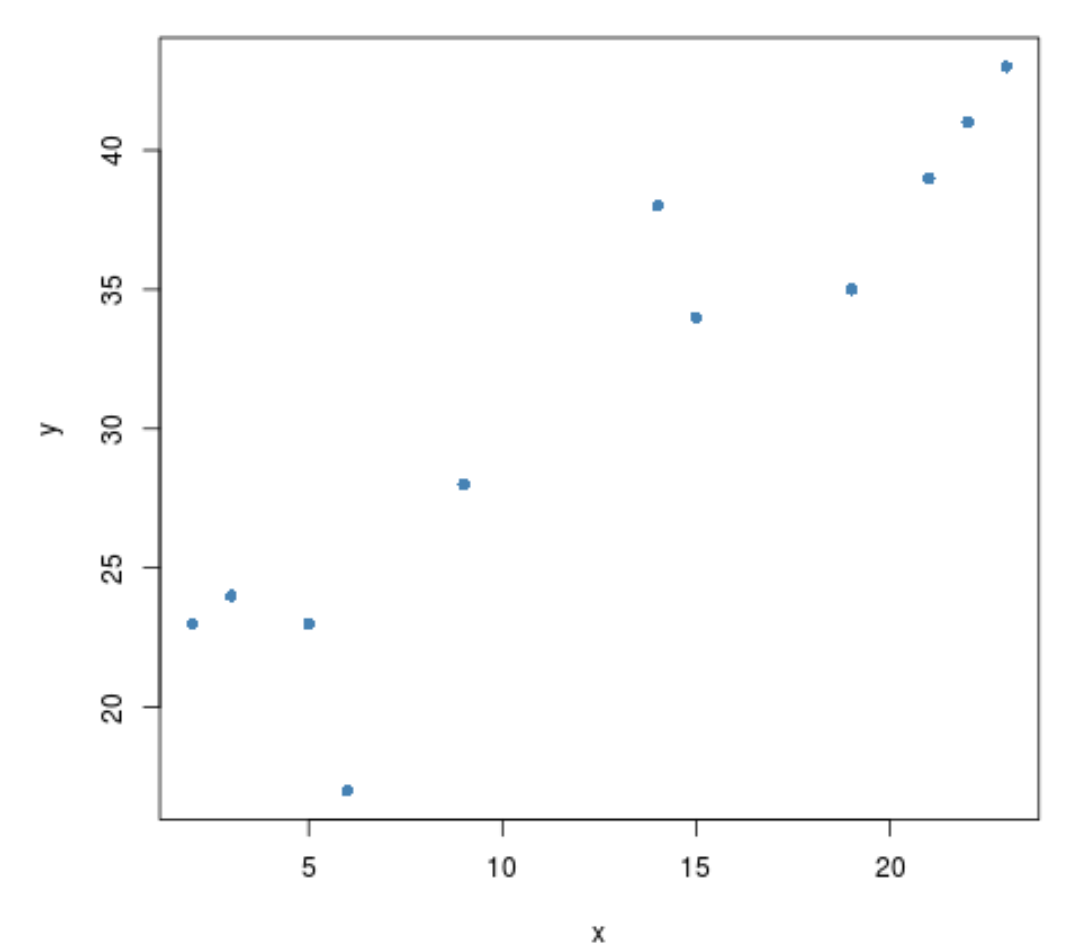
Er lijkt een positieve correlatie te bestaan tussen de twee variabelen. Dat wil zeggen: als de één toeneemt, zal de ander ook toenemen.

Om te zien of deze correlatie statistisch significant is, kunnen we een correlatietest uitvoeren:

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

De correlatiecoëfficiënt tussen de twee vectoren blijkt 0,9279869 te zijn.

De teststatistiek blijkt 7,8756 te zijn en de bijbehorende p-waarde is 1,35e-05 .

Omdat deze waarde kleiner is dan 0,05, hebben we voldoende bewijs om te zeggen dat de correlatie tussen de twee variabelen statistisch significant is.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over correlatiecoëfficiënten:

Een inleiding tot de Pearson-correlatiecoëfficiënt
Wat wordt beschouwd als een “sterke” correlatie?
De vijf hypothesen van Pearson’s correlatie