Covariantie

Von Dr.benjamin anderson August 5, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat covariantie is en hoe deze wordt berekend. U vindt de covariantieformule en een voorbeeld van het berekenen van de covariantie van een dataset. Bovendien kunt u aan het einde de covariantie van elke gegevensreeks berekenen met de online calculator.

Wat is covariantie?

In de statistiek is covariantie een waarde die de mate van gezamenlijke variatie van twee willekeurige variabelen aangeeft. Met andere woorden, covariantie wordt gebruikt om de afhankelijkheid tussen twee variabelen te analyseren.

De covariantie is gelijk aan de som van de producten van de verschillen tussen de gegevens van de twee variabelen en hun respectieve gemiddelden, gedeeld door het totale aantal gegevens.

👉 U kunt de onderstaande rekenmachine gebruiken om de covariantie van elke dataset te berekenen.

De interpretatie van de covariantiewaarde is heel eenvoudig:

Als de covariantie positief is , betekent dit dat er een afhankelijkheid bestaat tussen de twee variabelen. Wanneer de ene variabele in waarde stijgt, neemt de andere variabele dus ook toe, en omgekeerd.
Als de covariantie negatief is , betekent dit dat de relatie tussen de twee variabelen negatief is. Dus wanneer de ene variabele in waarde stijgt, neemt de andere variabele af, en omgekeerd.
Als de covariantie nul is (of de waarde ervan dichtbij nul ligt), betekent dit dat er geen verband bestaat tussen de twee variabelen. Met andere woorden: de twee willekeurige variabelen zijn onafhankelijk.

Hoe covariantie te berekenen

Om de covariantie van een gegevensreeks te berekenen, moeten de volgende stappen worden uitgevoerd:

Bereken het gemiddelde van elke variabele afzonderlijk.
Zoek voor elke variabele het verschil tussen elk van de waarden en het gemiddelde van de variabele.
Vermenigvuldig de verschillen die in de vorige stap zijn berekend voor elk gegevenspunt.
Tel alle resultaten op die u in de vorige stap hebt verkregen.
Deel door het totale aantal gegevens. De verkregen waarde is de covariantie van de gegevensreeks.

Samenvattend is de formule voor het berekenen van de covariantie tussen twee variabelen als volgt:

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}$

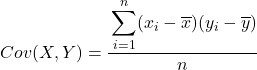
Een sterk aanbevolen methode om de covariantie tussen twee variabelen te extraheren, is door een tabel te maken met alle gegevensparen en een kolom toe te voegen voor elk van de hierboven uitgelegde stappen. Zo zijn uw berekeningen veel overzichtelijker en begrijpt u beter waar u mee bezig bent.

Voorbeeld van covariantieberekening

Gezien de definitie van covariantie vindt u hieronder een stapsgewijs voorbeeld van het berekenen van dit type statistische maatstaf. Het doel is dat u het concept van covariantie beter begrijpt en hoe u de correlatie tussen twee variabelen kunt analyseren.

Bereken de covariantie van de volgende statistische gegevensset:

Eerst moeten we het rekenkundig gemiddelde van elke variabele berekenen. Om dit te doen, delen we de som van de waarden van elke variabele door het totale aantal gegevens.

$\overline{x}=\cfrac{58}{10}=5,8$

$\overline{y}=\cfrac{51}{10}=5,1$

➤ Zie: rekenkundige formule gemiddelde

Zodra we het gemiddelde van elke willekeurige variabele hebben bepaald, kunnen we de volgende kolommen aan de gegevenstabel toevoegen om de covariantie te verkrijgen:

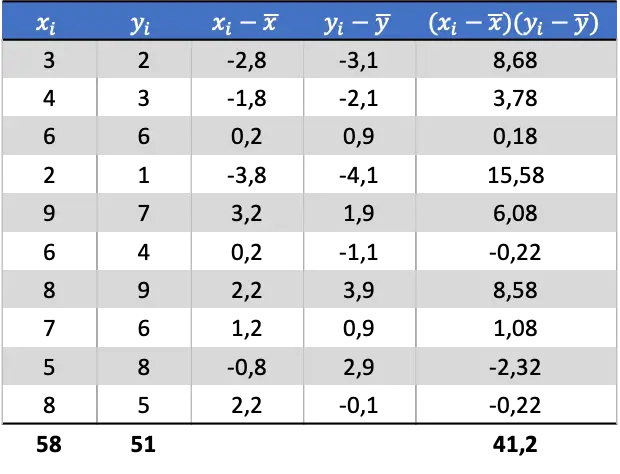
Om de covariantie van de twee variabelen te bepalen, moet u dus de som van de laatste kolom delen door het aantal gegevensparen:

$\begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}$

In dit geval is de covariantiewaarde positief, wat betekent dat er een directe afhankelijkheid bestaat tussen de twee onderzochte willekeurige variabelen. Als de covariantiewaarde echter negatief was geweest, zou dit betekenen dat de afhankelijkheid tussen de twee variabelen omgekeerd is. En ten slotte: als de covariantiewaarde nul of zeer dicht bij nul is, betekent dit dat er geen lineair verband bestaat tussen de twee variabelen.

Zoals u bij het oplossen van dit voorbeeld kunt zien, is het erg handig om een computerprogramma zoals Excel te gebruiken om de kolommen aan de tabel toe te voegen en de berekeningen snel uit te voeren. Anders duurt het veel langer om de covariantie te vinden door de bewerkingen handmatig te berekenen.

Covariantiecalculator

Voer een reeks statistische gegevens in de volgende rekenmachine in om de covariantie tussen twee variabelen te berekenen. U moet de gegevensparen scheiden, zodat in het eerste vak alleen de waarden van één variabele staan en in het tweede vak alleen de waarden van de tweede variabele.

Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Covariantie-eigenschappen

Covariantie heeft de volgende eigenschappen:

De covariantie tussen een willekeurige variabele en een constante is nul.

$Cov(X,a)=0$

De covariantie van een variabele en zichzelf is gelijk aan de variantie van die variabele.

$Cov(X,X)=Var(X)$

➤ Zie: wat is variantie?

De covariantie voldoet aan de symmetrie-eigenschap, dus de covariantie van variabelen X en Y is gelijk aan de covariantie van variabelen Y en X. De volgorde van de variabelen heeft geen invloed op het resultaat van de covariantie.

$Cov(X,Y)=Cov(Y,X)$

Als de variabelen met constanten worden vermenigvuldigd, kunt u eerst de covariantie berekenen en vervolgens het resultaat met de constanten vermenigvuldigen.

$Cov(a\cdot X,b\cdot Y)=a\cdot b\cdot Cov(X,Y)$

Het toevoegen van termen aan variabelen heeft geen invloed op het covariantieresultaat.

$Cov(a+X,b+Y)=Cov(X+Y)$

De covariantie tussen twee willekeurige variabelen houdt verband met hun wiskundige verwachtingen. De covariantie tussen de variabelen X en Y is gelijk aan de wiskundige verwachting van het product van X en Y minus het product van de wiskundige verwachting van elke variabele.

$Cov(X,Y)=E[X\cdot Y]-E[X]\cdot E[Y]$

Bij het werken met variabelen wordt de volgende algebraïsche uitdrukking gevuld met betrekking tot covariantie:

$\begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}$

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder