Cumulatieve relatieve frequentie

In dit artikel wordt uitgelegd wat cumulatieve relatieve frequentie in statistieken is. U vindt dus de definitie van cumulatieve relatieve frequentie, hoe u de cumulatieve relatieve frequentie kunt verkrijgen en twee oefeningen die stap voor stap worden opgelost.

Wat is cumulatieve relatieve frequentie?

In de statistieken is de cumulatieve relatieve frequentie de cumulatieve som van relatieve frequenties. Dat wil zeggen dat de cumulatieve relatieve frequentie van een waarde gelijk is aan de relatieve frequentie van die waarde plus de relatieve frequenties van alle waarden die kleiner zijn dan deze.

Het symbool voor cumulatieve relatieve frequentie is _Hi . In de statistieken bestaat er echter nog geen volledige consensus over het symbool voor dit type frequentie, en daarom kan het ook voorkomen dat het wordt uitgedrukt met een ander symbool.

Om de betekenis van cumulatieve relatieve frequentie te begrijpen, moet je uiteraard eerst duidelijk zijn over het concept van relatieve frequentie. Daarom raad ik je aan de volgende link te bezoeken voordat je doorgaat met de uitleg:

Hoe de cumulatieve relatieve frequentie te berekenen

Om de cumulatieve relatieve frequentie te berekenen, moeten de volgende stappen worden gevolgd:

1. Construeer een frequentietabel met alle verschillende waarden uit de statistische steekproef.
2. Bereken de absolute frequentie van elke waarde.
3. Bepaal uit de absolute frequenties de relatieve frequentie van elke waarde.
4. Zoek de cumulatieve relatieve frequentie van elke waarde, die wordt berekend door de relatieve frequentie van de waarde zelf op te tellen plus de relatieve frequenties van alle kleinere waarden.

Houd er rekening mee dat als u het cumulatieve relatieve frequentiepercentage wilt berekenen, dat wil zeggen de cumulatieve relatieve frequentie uitgedrukt als een percentage, u gewoon dezelfde stappen hoeft te volgen en de resultaten met 100 moet vermenigvuldigen.

Voorbeelden van cumulatieve relatieve frequentie

Om u te laten zien hoe de cumulatieve relatieve frequentie wordt berekend, worden hieronder twee voorbeelden weergegeven die stap voor stap zijn opgelost. In het eerste voorbeeld vinden we de cumulatieve relatieve frequentie van een discrete variabele en in het tweede voorbeeld een continue variabele, aangezien het proces enigszins varieert.

Voorbeeld 1: discrete variabele

• De cijfers behaald voor het vak statistiek in een klas van 30 studenten zijn als volgt. Wat is de cumulatieve relatieve frequentie van elke noot?

In dit geval is de variabele discreet, omdat deze geen decimale waarde kan aannemen. Het is daarom niet nodig om de gegevens op intervallen te groeperen, maar de berekeningen kunnen direct worden uitgevoerd.

We stellen dus een frequentietabel op en bepalen de absolute frequentie van elke verschillende waarde:

Vervolgens berekenen we de relatieve frequentie van elke waarde (je kunt zien hoe dit wordt gedaan in de link aan het begin van het bericht).

En zodra we de absolute frequentie en relatieve frequentie van de dataset hebben berekend, kunnen we de cumulatieve relatieve frequentie krijgen. Om dit te doen, moeten we de relatieve frequentie van de betreffende waarde optellen plus alle voorgaande relatieve frequenties of, met andere woorden, de vorige geaccumuleerde relatieve frequentie:

Kort gezegd ziet de frequentietabel met absolute frequentie, relatieve frequentie en cumulatieve relatieve frequentie er als volgt uit:

Houd er rekening mee dat de laatste waarde van de cumulatieve relatieve frequentie altijd 1 moet zijn. Als u een ander getal krijgt, betekent dit dat u een fout heeft gemaakt in de berekeningen.

Voorbeeld 2: continue variabele

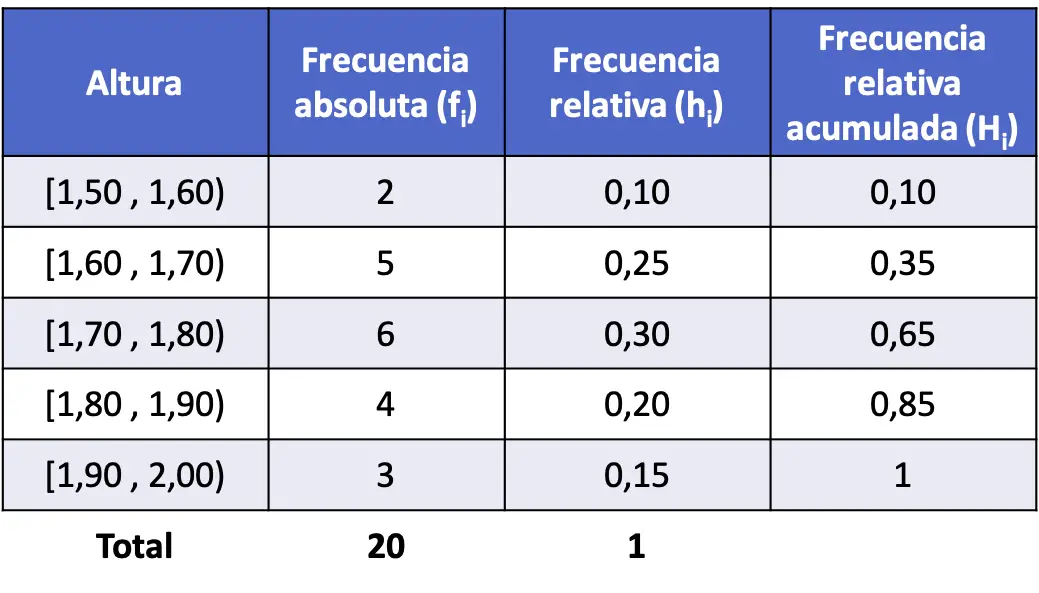
• De lengte van 20 personen werd gemeten en de onderstaande resultaten werden verkregen. Verdeel de gegevens in intervallen en vind de cumulatieve relatieve frequentie van elk interval.

Dit geval verschilt van het vorige probleem, omdat de getallen decimaal zijn, wat betekent dat de variabele elke waarde kan aannemen en daarom continu is. We zullen daarom de frequentietabel maken door de gegevens in intervallen te groeperen.

We construeren daarom de tabel en verkrijgen de absolute frequentie van elk interval:

We berekenen nu de relatieve frequenties door de absolute frequentie van elk interval te delen door het totale aantal datapunten:

En tenslotte vinden we de cumulatieve relatieve frequenties van alle intervallen. Om een cumulatieve relatieve frequentie van een interval te bepalen, is het, net als voorheen, noodzakelijk om de relatieve frequentie van dat interval plus de voorgaande relatieve frequenties op te tellen:

Cumulatieve relatieve frequentie en cumulatieve absolute frequentie

We hebben zojuist gezien hoe de cumulatieve relatieve frequentie wordt afgeleid van de relatieve frequentie. Dit type frequentie kan echter ook worden gevonden met behulp van de cumulatieve absolute frequentie.

De cumulatieve relatieve frequentie kan worden berekend door de cumulatieve absolute frequentie te delen door het totale aantal gegevens in de steekproef.

Daarom is de formule voor de cumulatieve relatieve frequentie :

Goud:

• 

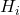
  is de cumulatieve relatieve frequentie.

• 

  is de geaccumuleerde absolute frequentie .

• 

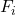
  is het totale aantal gegevens.

In navolging van het eerste hierboven ontwikkelde voorbeeld, wordt hier de manier gevonden waarop de geaccumuleerde relatieve frequentie wordt gevonden op basis van de geaccumuleerde absolute frequentie:

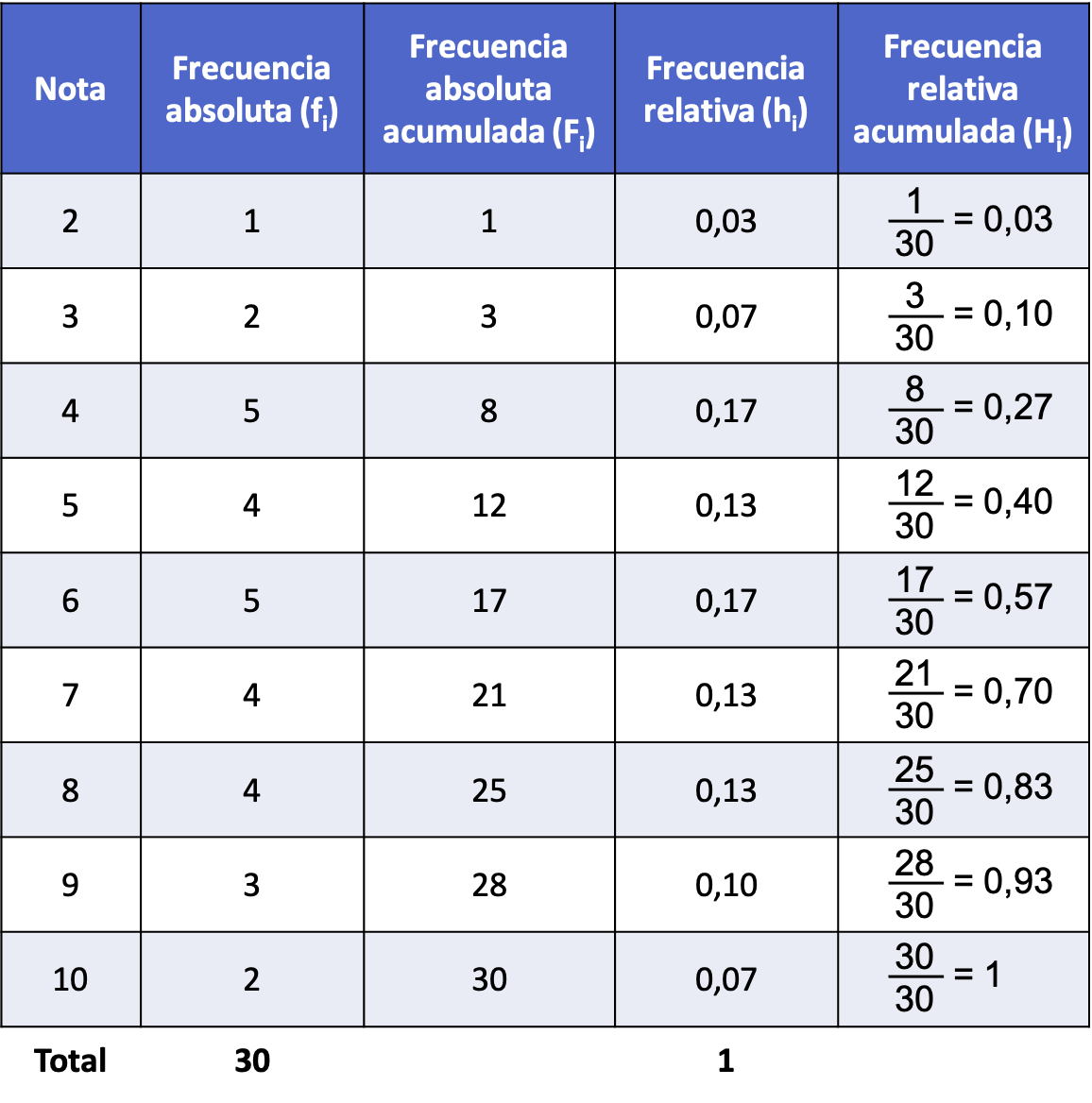
Omdat de bovenstaande tabel alle soorten statistische frequenties bevat, wordt deze een frequentietabel genoemd. Klik hier voor meer informatie: