Curve-aanpassing in excel (met voorbeelden)

Vaak wilt u misschien de vergelijking vinden die het beste past bij een curve voor een reeks gegevens in Excel.

Gelukkig is dit vrij eenvoudig te doen met de Trendline- functie van Excel.

Deze zelfstudie biedt een stapsgewijs voorbeeld van hoe u een vergelijking aan een curve in Excel kunt aanpassen.

Stap 1: Creëer de gegevens

Laten we eerst een nep-dataset maken om mee te werken:

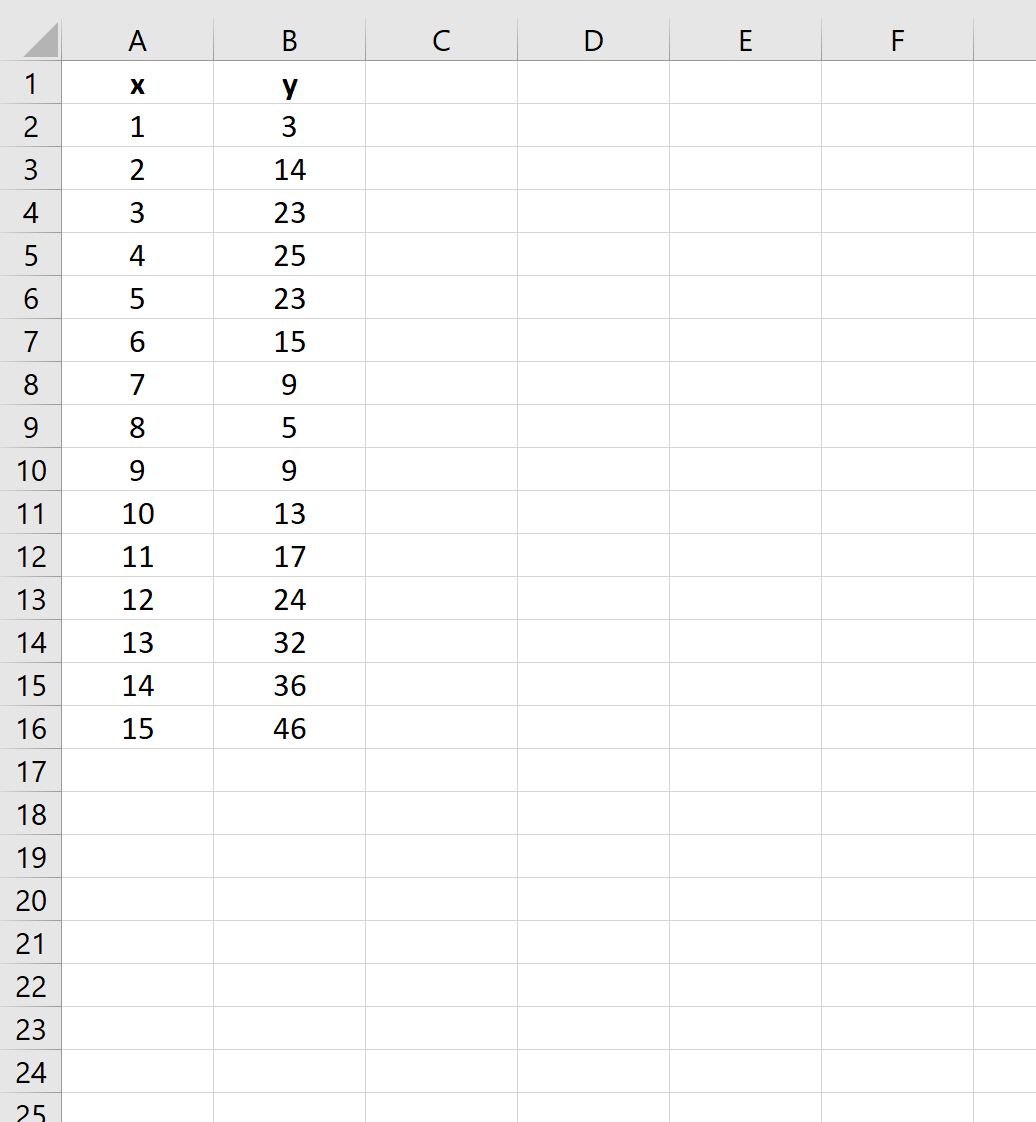
Stap 2: Maak een spreidingsdiagram

Laten we vervolgens een spreidingsdiagram maken om de gegevensset te visualiseren.

Markeer eerst de cellen A2:B16 als volgt:

Klik vervolgens op het tabblad Invoegen langs het bovenste lint en klik vervolgens op de eerste plotoptie onder Spreiding :

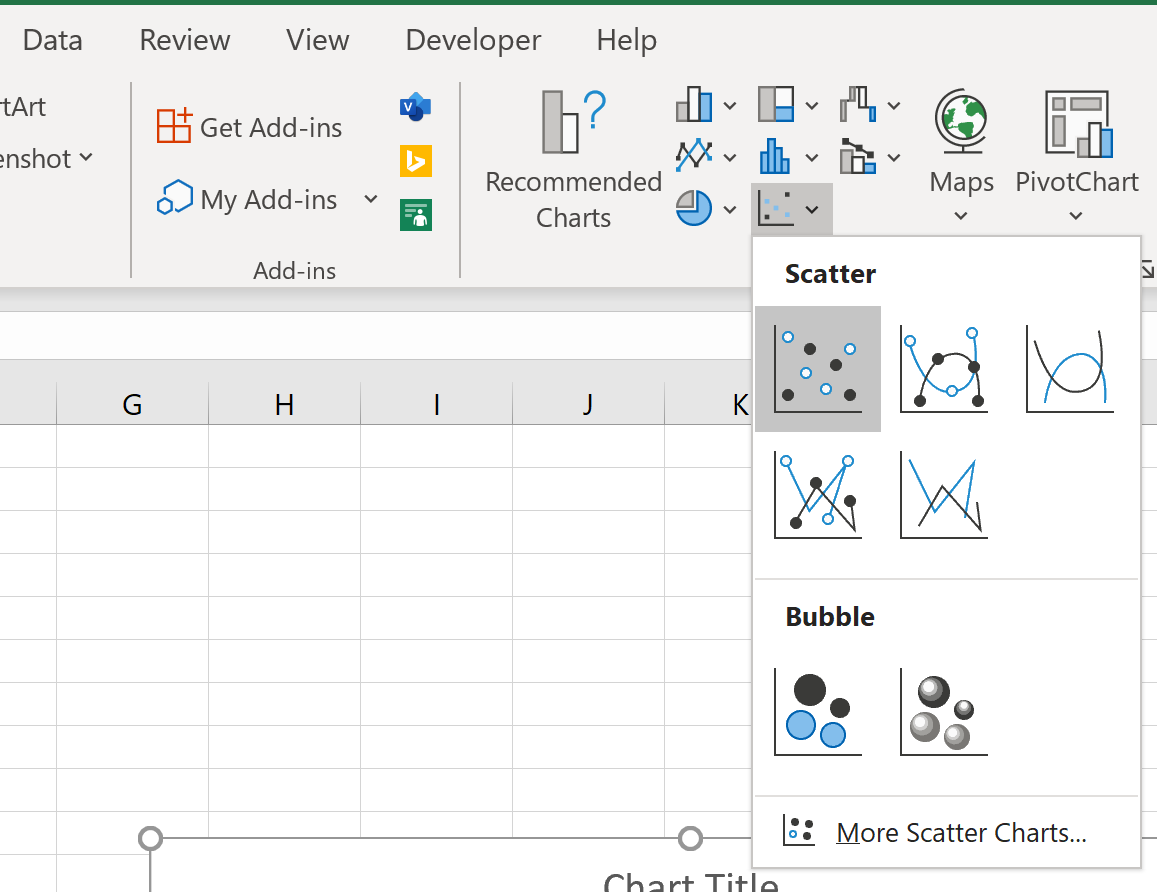
Dit levert het volgende spreidingsdiagram op:

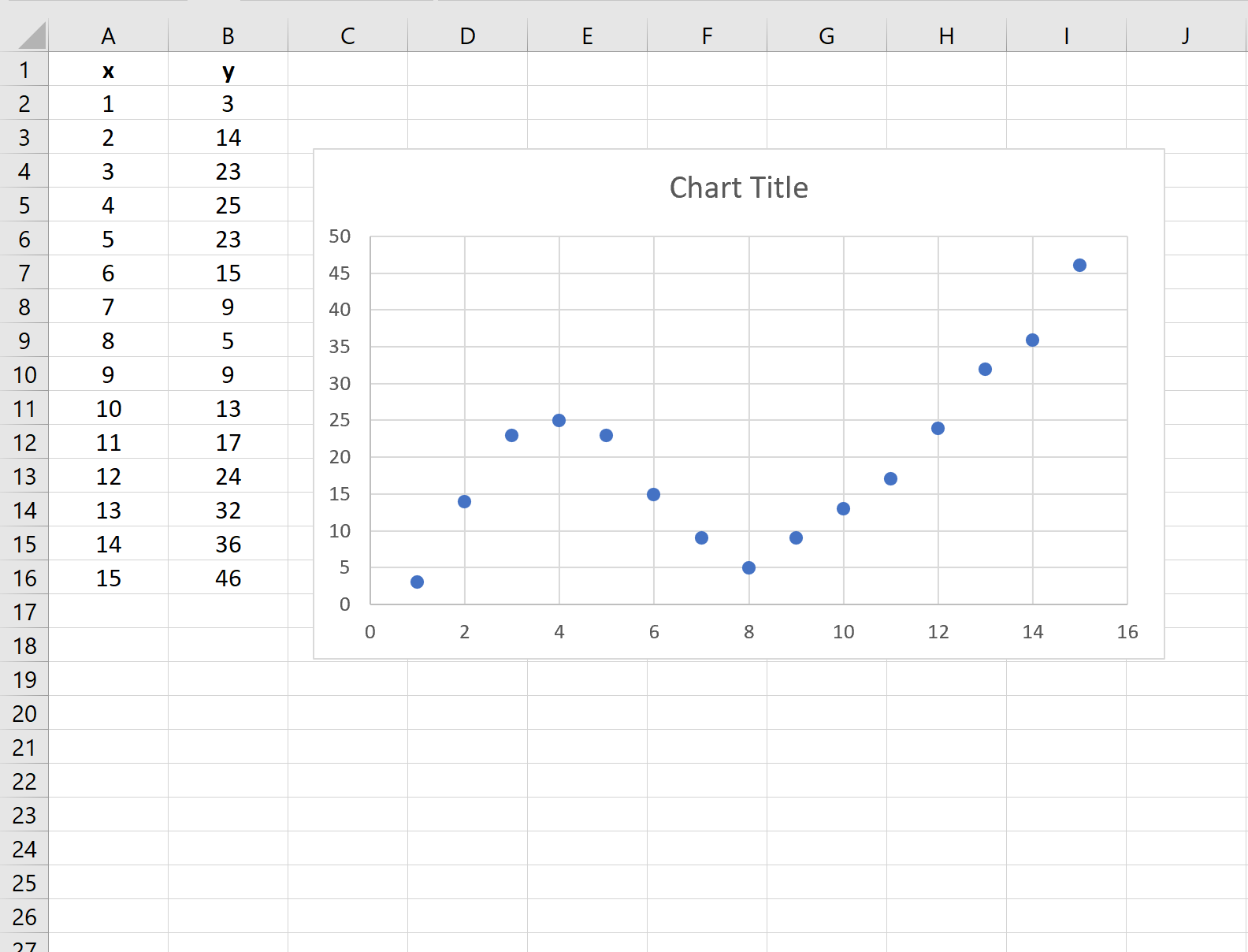
Stap 3: Voeg een trendlijn toe

Klik vervolgens ergens op het spreidingsdiagram. Klik vervolgens op het + teken in de rechterbovenhoek. Klik in het vervolgkeuzemenu op de pijl naast Trendlijn en klik vervolgens op Meer opties :

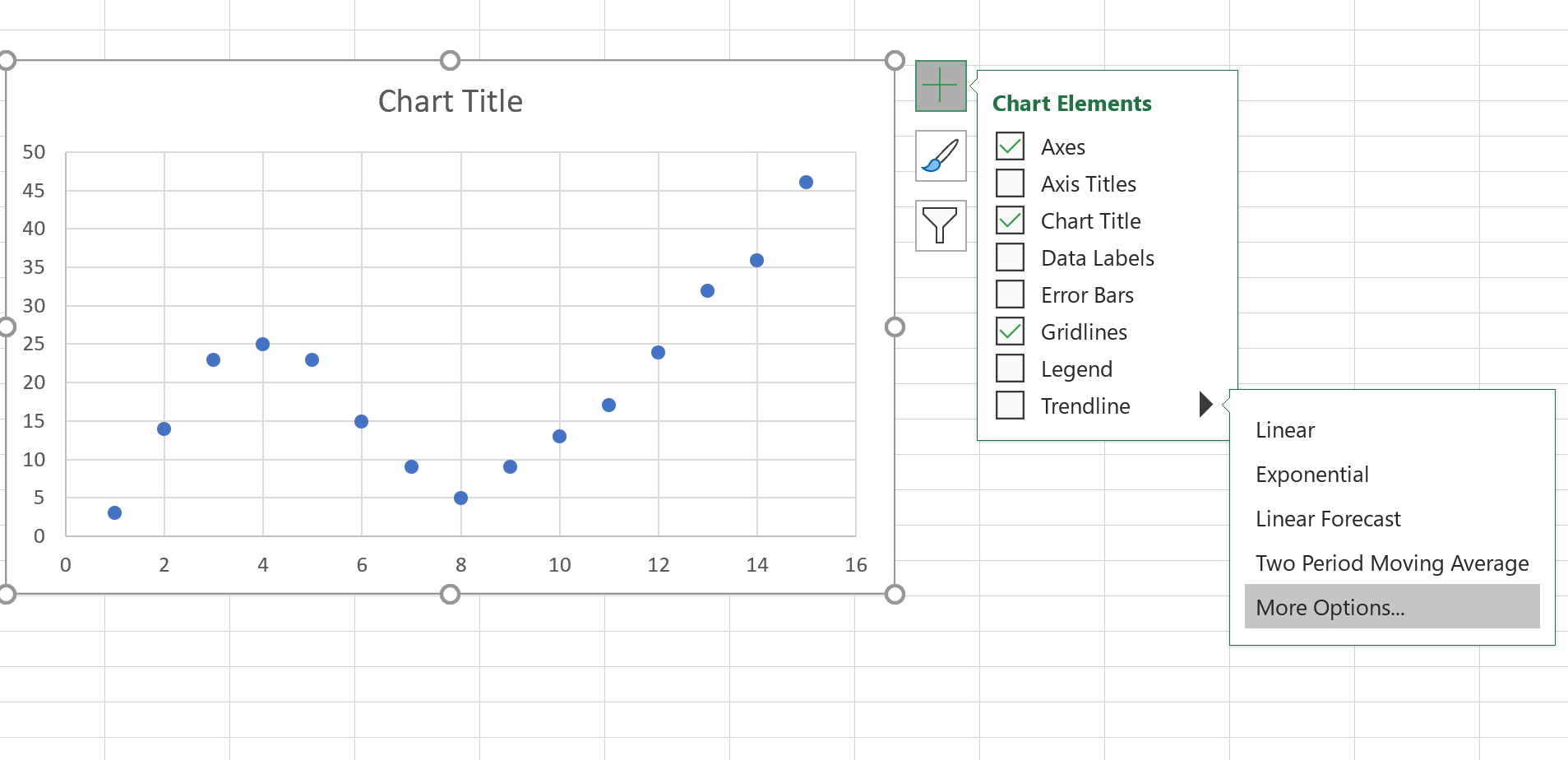
In het venster dat aan de rechterkant verschijnt, klikt u op de knop naast Polynoom . Vink vervolgens de vakjes aan naast Vergelijking weergeven in diagram en R-kwadraatwaarde weergeven in diagram .

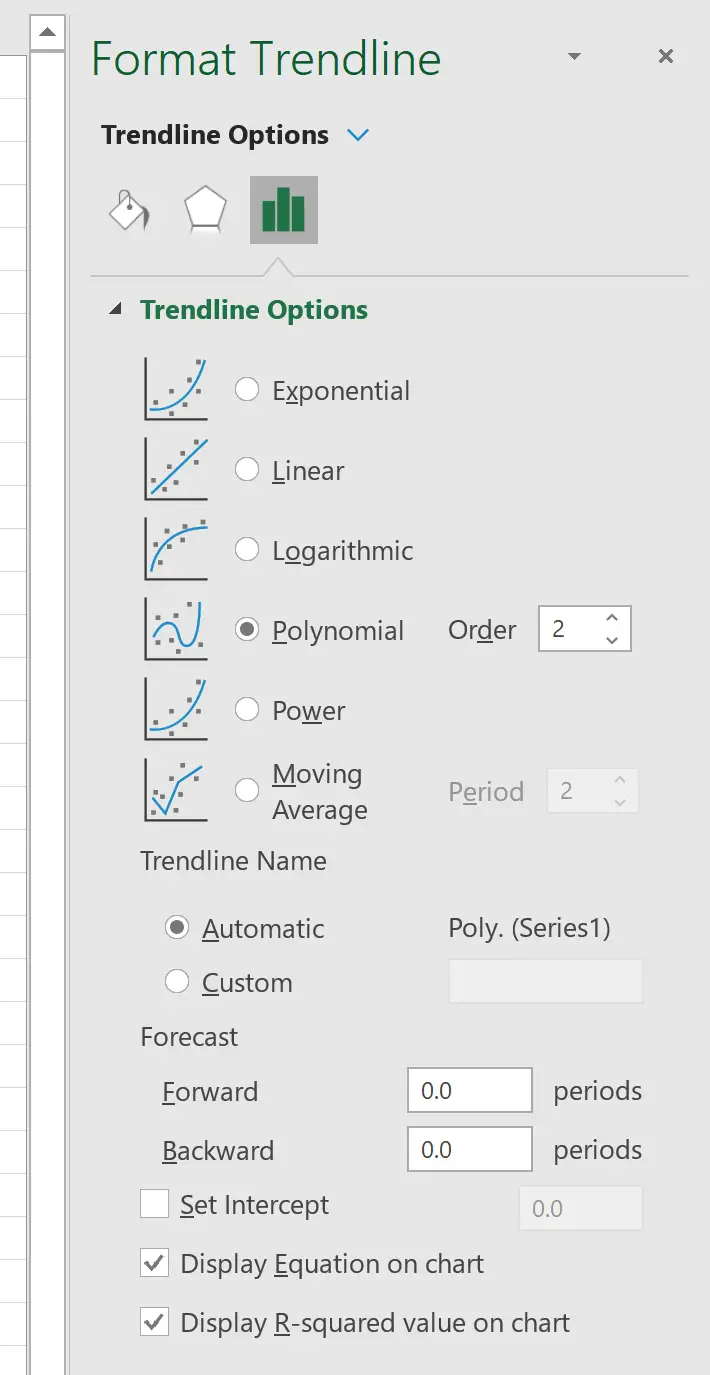
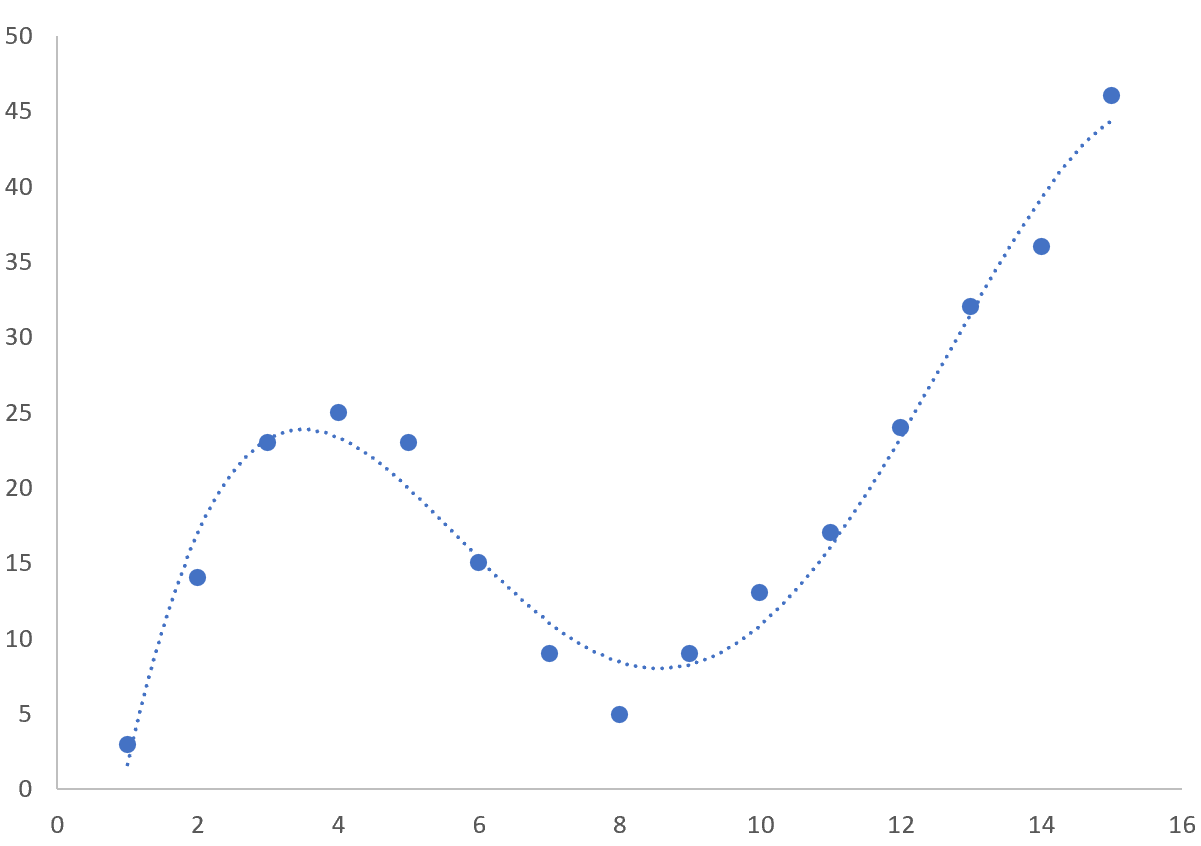
Dit levert de volgende curve op de puntenwolk op:

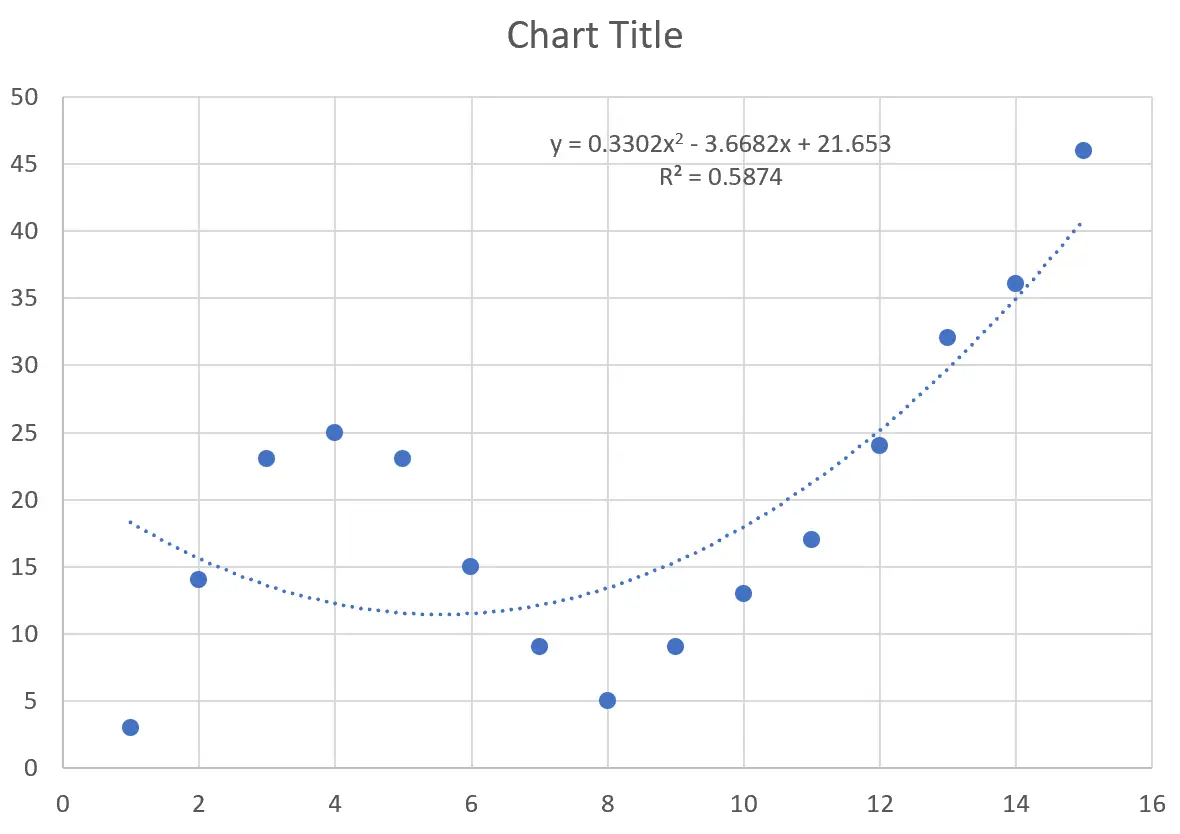
De vergelijking van de curve is als volgt:

y = 0,3302x ² – 3,6682x + 21,653

De R-kwadraat vertelt ons het percentage variatie in deresponsvariabele dat kan worden verklaard door de voorspellende variabelen. De R-kwadraat voor deze specifieke curve is 0,5874 .

Stap 4: Kies de beste trendlijn

We kunnen ook de volgorde van de polynoom die we gebruiken verhogen om te zien of een flexibelere curve beter bij de dataset past.

We kunnen er bijvoorbeeld voor kiezen om de polynoomvolgorde in te stellen op 4:

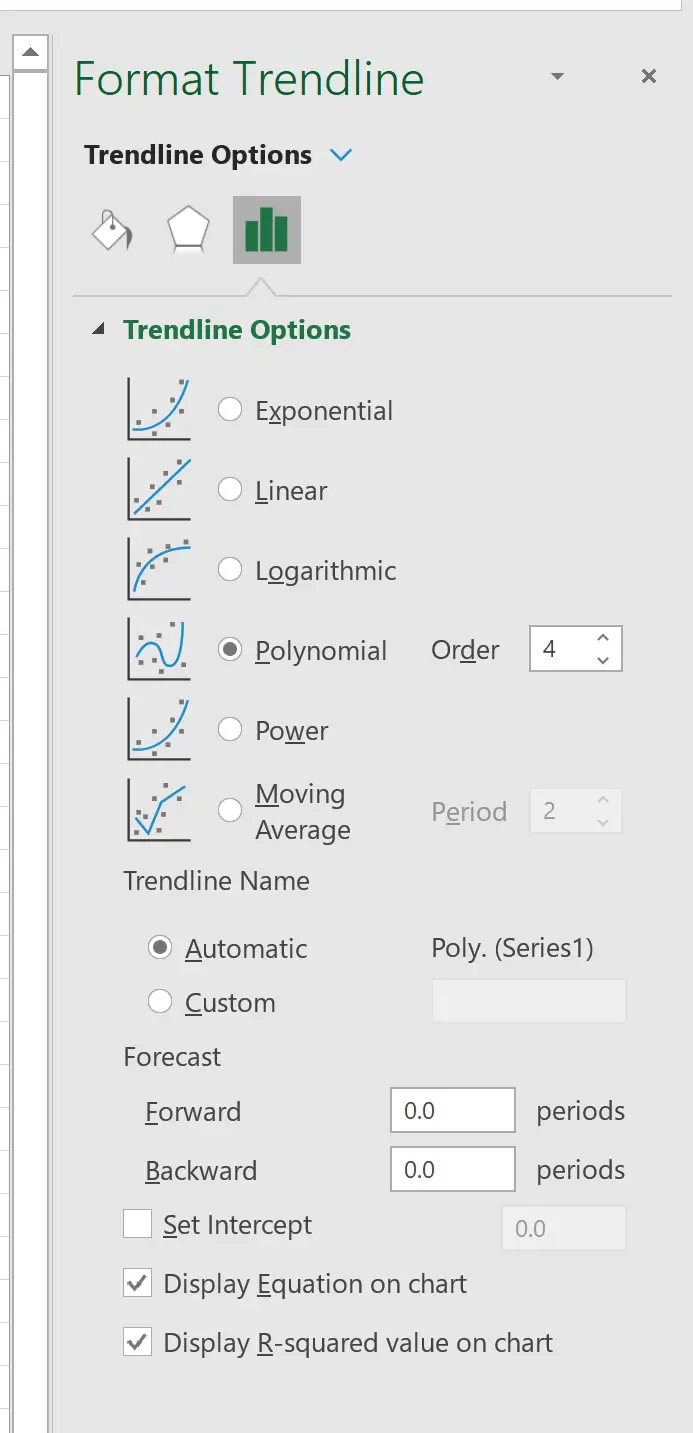
Dit resulteert in de volgende curve:

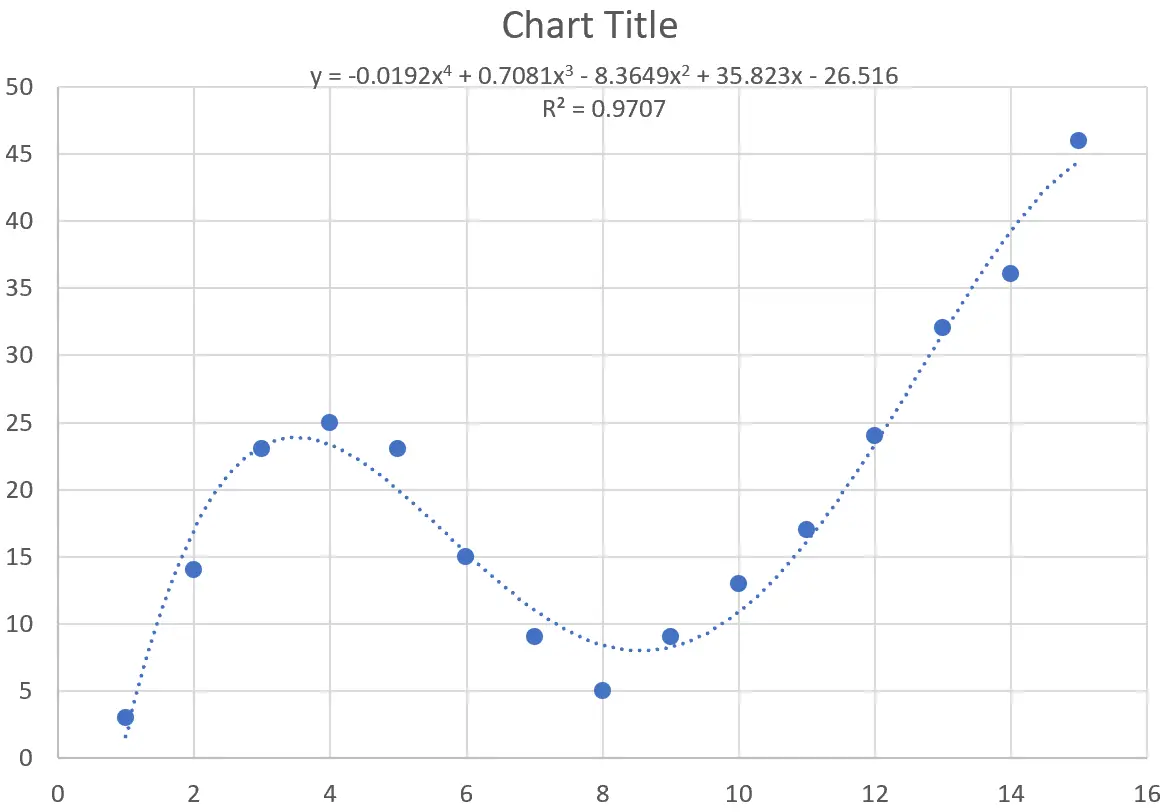
De vergelijking van de curve is als volgt:

y = -0,0192x ⁴ + 0,7081x ³ – 8,3649x ² + 35,823x – 26,516

De R-kwadraat voor deze specifieke curve is 0,9707 .

Deze R-kwadraat is aanzienlijk hoger dan die van de vorige curve, wat aangeeft dat deze veel beter overeenkomt met de dataset.

We kunnen deze curvevergelijking ook gebruiken om de waarde van de responsvariabele te voorspellen op basis van de voorspellende variabele. Als x = 4 bijvoorbeeld, voorspellen we dat y = 23,34 :

y = -0,0192(4) ⁴ + 0,7081(4) ³ – 8,3649(4) ² + 35,823(4) – 26,516 = 23,34

Op deze pagina vindt u meer Excel-tutorials.