Hoe anova-aannames te controleren
Een one-way ANOVA is een statistische test die wordt gebruikt om te bepalen of er al dan niet een significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.
Hier is een voorbeeld van wanneer we een eenrichtings-ANOVA kunnen gebruiken:
Een klas van 90 studenten verdeel je willekeurig in drie groepen van 30. Elke groep gebruikt een maand lang een andere studietechniek ter voorbereiding op een examen. Aan het einde van de maand leggen alle studenten hetzelfde examen af.
Je wilt weten of studietechniek invloed heeft op de examenscores. Je voert dus een one-way ANOVA uit om te bepalen of er een statistisch significant verschil is tussen de gemiddelde scores van de drie groepen.
Voordat we een eenrichtings-ANOVA kunnen uitvoeren, moeten we eerst verifiëren dat aan drie aannames is voldaan.
1. Normaliteit – Elke steekproef werd getrokken uit een normaal verdeelde populatie.
2. Gelijke varianties – De varianties van de populaties waaruit de steekproeven zijn getrokken, zijn gelijk.
3. Onafhankelijkheid – De waarnemingen binnen elke groep zijn onafhankelijk van elkaar en de waarnemingen binnen de groepen zijn verkregen door middel van willekeurige steekproeven.
Als niet aan deze aannames wordt voldaan, zijn de resultaten van onze eenrichtings-ANOVA mogelijk niet betrouwbaar.
In dit artikel leggen we uit hoe u deze aannames kunt controleren en wat u moet doen als een van deze aannames wordt geschonden.
Aanname #1: normaliteit
ANOVA gaat ervan uit dat elke steekproef afkomstig is uit een normaal verdeelde populatie.
Hoe deze hypothese in R te controleren:
Om deze hypothese te verifiëren, kunnen we twee benaderingen gebruiken:
- Verifieer de hypothese visueel met behulp van histogrammen of QQ-plots .
- Verifieer de hypothese met behulp van formele statistische tests zoals Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre of D’Agostino-Pearson.
Stel dat we bijvoorbeeld 90 mensen rekruteren om deel te nemen aan een gewichtsverliesexperiment waarbij we willekeurig 30 mensen toewijzen om Programma A, Programma B of Programma C gedurende één maand te volgen. Om te zien of het programma impact heeft op gewichtsverlies, willen we een one-way ANOVA uitvoeren. De volgende code laat zien hoe u de normaliteitsaanname kunt controleren met behulp van histogrammen, QQ-plots en een Shapiro-Wilk-test.
1. Monteer het ANOVA-model.
#make this example reproducible
set.seed(0)
#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
weight_loss = c(runif(30, 0, 3),
runif(30, 0, 5),
runif(30, 1, 7)))
#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)
2. Maak een histogram van de responswaarden.
#create histogram
hist(data$weight_loss)
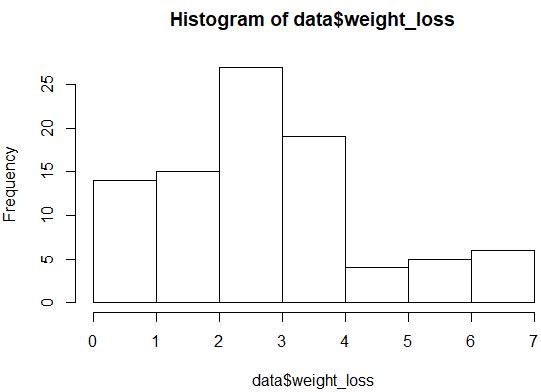
De verdeling ziet er niet erg normaal verdeeld uit (hij heeft bijvoorbeeld geen klokvorm), maar we kunnen ook een QQ-plot maken om de verdeling nog eens te bekijken.
3. Maak een QQ-plot van residuen
#create QQ plot to compare this dataset to a theoretical normal distribution qqnorm(model$residuals) #add straight diagonal line to plot qqline(model$residuals)

Als de datapunten in een QQ-plot langs een rechte diagonale lijn liggen, volgt de dataset in het algemeen waarschijnlijk een normale verdeling. In dit geval kunnen we zien dat er een merkbare afwijking is van de lijn langs de uiteinden, wat erop zou kunnen wijzen dat de gegevens niet normaal verdeeld zijn.
4. Voer de Shapiro-Wilk-test uit voor normaliteit.
#Conduct Shapiro-Wilk Test for normality shapiro. test (data$weight_loss) #Shapiro-Wilk normality test # #data: data$weight_loss #W = 0.9587, p-value = 0.005999
De Shapiro-Wilk-test toetst de nulhypothese dat de steekproeven uit een normale verdeling komen, tegenover de alternatieve hypothese dat de steekproeven niet uit een normale verdeling komen. In dit geval is de p-waarde van de test 0,005999 , wat lager is dan het alfaniveau van 0,05. Dit suggereert dat de steekproeven geen normale verdeling volgen.
Wat te doen als deze veronderstelling niet wordt gerespecteerd:
Over het algemeen wordt een eenrichtings-ANOVA als behoorlijk robuust beschouwd tegen schendingen van de normaliteitsaanname, zolang de steekproefomvang groot genoeg is.
Als u extreem grote steekproeven heeft, zullen statistische tests zoals de Shapiro-Wilk-test u bovendien bijna altijd vertellen dat uw gegevens niet normaal zijn. Om deze reden is het vaak het beste om uw gegevens visueel te inspecteren met behulp van grafieken zoals histogrammen en QQ-plots. Door alleen maar naar de grafieken te kijken, kun je een redelijk goed idee krijgen of de gegevens normaal verdeeld zijn of niet.
Als de aanname van normaliteit ernstig wordt geschonden of als je gewoon heel conservatief wilt zijn, heb je twee keuzes:
(1) Transformeer de responswaarden van uw gegevens zodat de verdelingen normaler verdeeld zijn.
(2) Voer een gelijkwaardige niet-parametrische test uit, zoals een Kruskal-Wallis-test waarvoor geen aanname van normaliteit vereist is.
Aanname #2: gelijke variantie
ANOVA gaat ervan uit dat de varianties van de populaties waaruit de steekproeven worden getrokken gelijk zijn.
Hoe deze hypothese in R te controleren:
We kunnen deze hypothese in R verifiëren met behulp van twee benaderingen:
- Controleer de hypothese visueel met behulp van boxplots.
- Test de hypothese met behulp van formele statistische tests zoals de test van Bartlett.
De volgende code laat zien hoe u dit kunt doen, met behulp van dezelfde nepgegevensset voor gewichtsverlies die we eerder hebben gemaakt.
1. Maak boxplots.
#Create box plots that show distribution of weight loss for each group boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)
De variantie in gewichtsverlies in elke groep kan worden waargenomen aan de hand van de lengte van elke boxplot. Hoe langer het vakje, hoe hoger de variantie. We kunnen bijvoorbeeld zien dat de variantie iets hoger is voor deelnemers aan Programma C vergeleken met Programma A en Programma B.
2. Voer de Bartlett-test uit.
#Create box plots that show distribution of weight loss for each group bartlett. test (weight_loss ~ program, data=data) #Bartlett test of homogeneity of variances # #data: weight_loss by program #Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599
De Bartlett-test test de nulhypothese dat de steekproeven gelijke varianties hebben, tegenover de alternatieve hypothese dat de steekproeven geen gelijke varianties hebben. In dit geval is de p-waarde van de test 0,01599 , wat lager is dan het alfaniveau van 0,05. Dit suggereert dat de monsters niet allemaal dezelfde variantie hebben.
Wat te doen als deze veronderstelling niet wordt gerespecteerd:
Over het algemeen wordt een eenrichtings-ANOVA als redelijk robuust beschouwd voor schendingen van de aanname van gelijke varianties, zolang elke groep dezelfde steekproefomvang heeft.
Als de steekproefomvang echter niet hetzelfde is en deze aanname ernstig wordt geschonden, kunt u in plaats daarvan een Kruskal-Wallis-test uitvoeren, de niet-parametrische versie van eenrichtings-ANOVA.
Veronderstelling #3: Onafhankelijkheid
ANOVA gaat ervan uit:
- De waarnemingen van elke groep zijn onafhankelijk van de waarnemingen van alle andere groepen.
- Waarnemingen binnen elke groep werden verkregen door een willekeurige steekproef.
Hoe deze hypothese te verifiëren:
Er bestaat geen formele test die je kunt gebruiken om te verifiëren dat de waarnemingen in elke groep onafhankelijk zijn en dat ze door een willekeurige steekproef zijn verkregen. De enige manier om aan deze veronderstelling te voldoen is door gebruik te maken van een gerandomiseerd ontwerp.
Wat te doen als deze veronderstelling niet wordt gerespecteerd:
Helaas kunt u niet veel doen als niet aan deze veronderstelling wordt voldaan. Simpel gezegd: als de gegevens op een zodanige manier zijn verzameld dat de waarnemingen in elke groep niet onafhankelijk zijn van de waarnemingen in andere groepen, of als de waarnemingen binnen elke groep niet via een gerandomiseerd proces zijn verkregen, zullen de ANOVA-resultaten niet betrouwbaar zijn. .
Als niet aan deze veronderstelling wordt voldaan, kun je het experiment het beste opnieuw uitvoeren met een gerandomiseerd ontwerp.
Verder lezen:
Eenrichtings-ANOVA uitvoeren in R
Eenrichtings-ANOVA uitvoeren in Excel
