Hoe residuen in een anova-model te analyseren
Een ANOVA (“variantieanalyse”) is een type model dat wordt gebruikt om te bepalen of er al dan niet een significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.
we passen een ANOVA aan. Wanneer een model ook aan een dataset wordt gekoppeld, zullen er altijd residuen zijn – deze vertegenwoordigen het verschil tussen elke individuele waarneming en het groepsgemiddelde waaruit de waarneming voortkwam.
Het volgende voorbeeld laat zien hoe u in de praktijk residuen voor een ANOVA-model kunt berekenen.
Voorbeeld: Berekening van residuen in ANOVA
Stel dat we 90 mensen rekruteren om deel te nemen aan een gewichtsverliesexperiment waarbij we willekeurig 30 mensen toewijzen om een maand lang Programma A, Programma B of Programma C te volgen.
We kunnen een one-way ANOVA uitvoeren om te bepalen of er een statistisch significant verschil is tussen het gewichtsverlies als gevolg van de drie programma’s.
Stel dat we het gemiddelde gewichtsverlies van personen die aan elk programma deelnemen, als volgt berekenen:
- Programma A : 1,58 pond
- Programma B : 2,56 pond
- Programma C : 4,13 pond
De residuen van het ANOVA-model zouden het verschil zijn tussen het gewichtsverlies van elk individu en het gemiddelde gewichtsverlies van hun programma.
De volgende tabel laat bijvoorbeeld zien hoe u de residuen kunt berekenen voor 10 verschillende personen in het onderzoek:
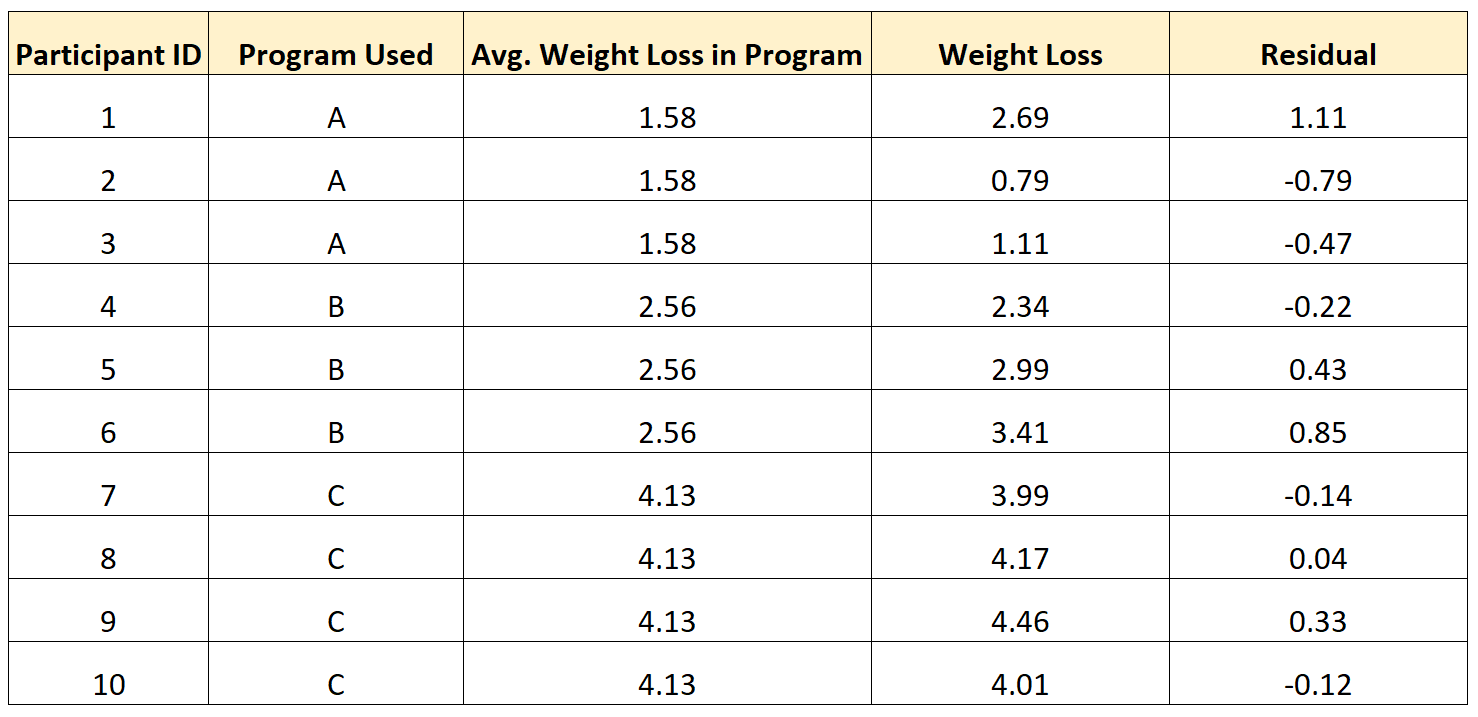
Let op het volgende patroon:
- Individuen met een waarde boven hun groepsgemiddelde hadden een positieve residu .
- Individuen met een waarde lager dan hun groepsgemiddelde hadden een negatief residu .
In de praktijk zouden we de residuen voor alle 90 individuen berekenen.
Hoe residuen te gebruiken om de normaliteit te controleren
Eén van de aannames van een ANOVA is dat de residuen normaal verdeeld zijn.
De meest gebruikelijke manier om deze aanname te verifiëren is door eenQQ-plot te maken.
Als de residuen normaal verdeeld zijn, liggen de punten op een QQ-plot op een rechte diagonale lijn.
Hier ziet u hoe een QQ-plot eruit zou zien voor ons vorige voorbeeld:
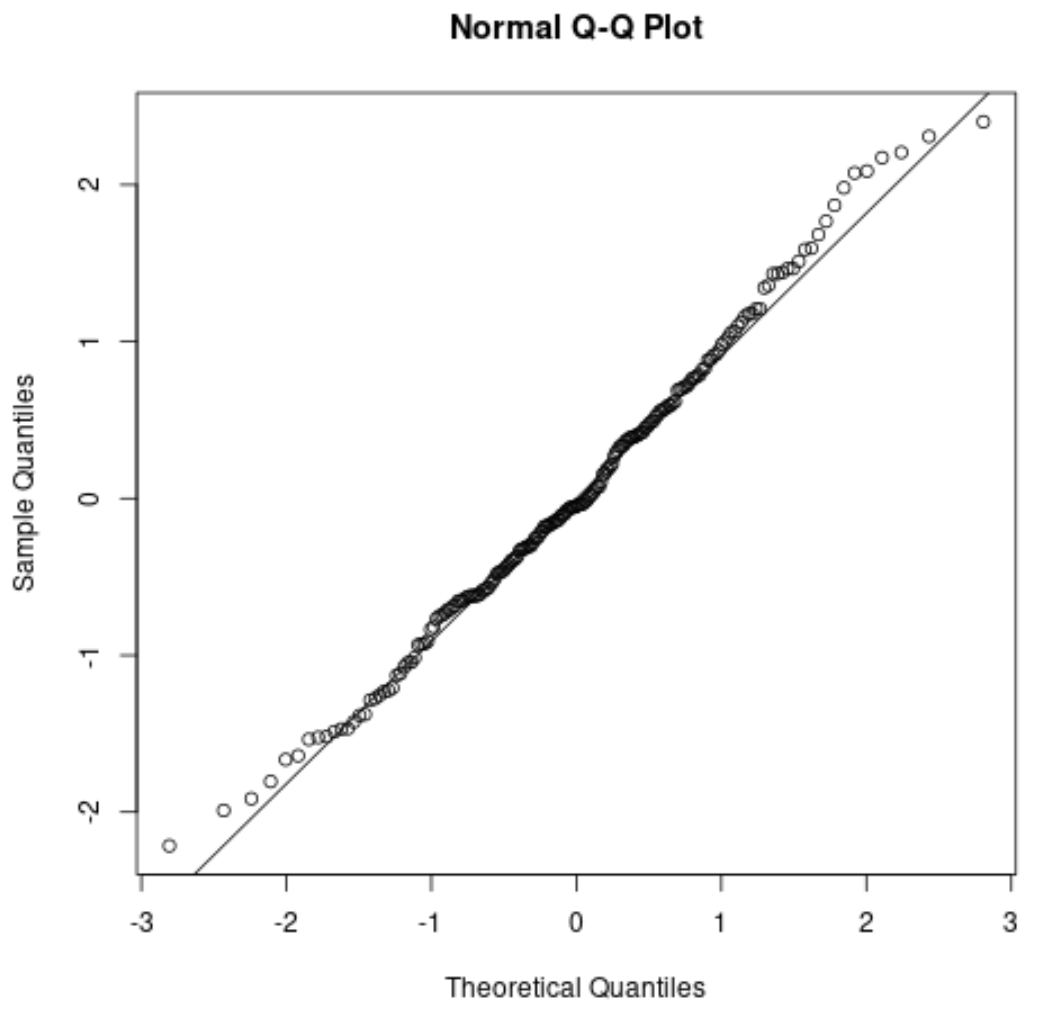
De punten wijken iets af van de rechte diagonale lijn aan de uiteinden van de staart, maar over het algemeen volgen de punten de diagonale lijn vrij goed. Dit vertelt ons dat waarschijnlijk aan de normaliteitsaanname is voldaan.
Ter referentie: hier is hoe een QQ-plot voor niet-normaal verdeelde residuen eruit zou kunnen zien:
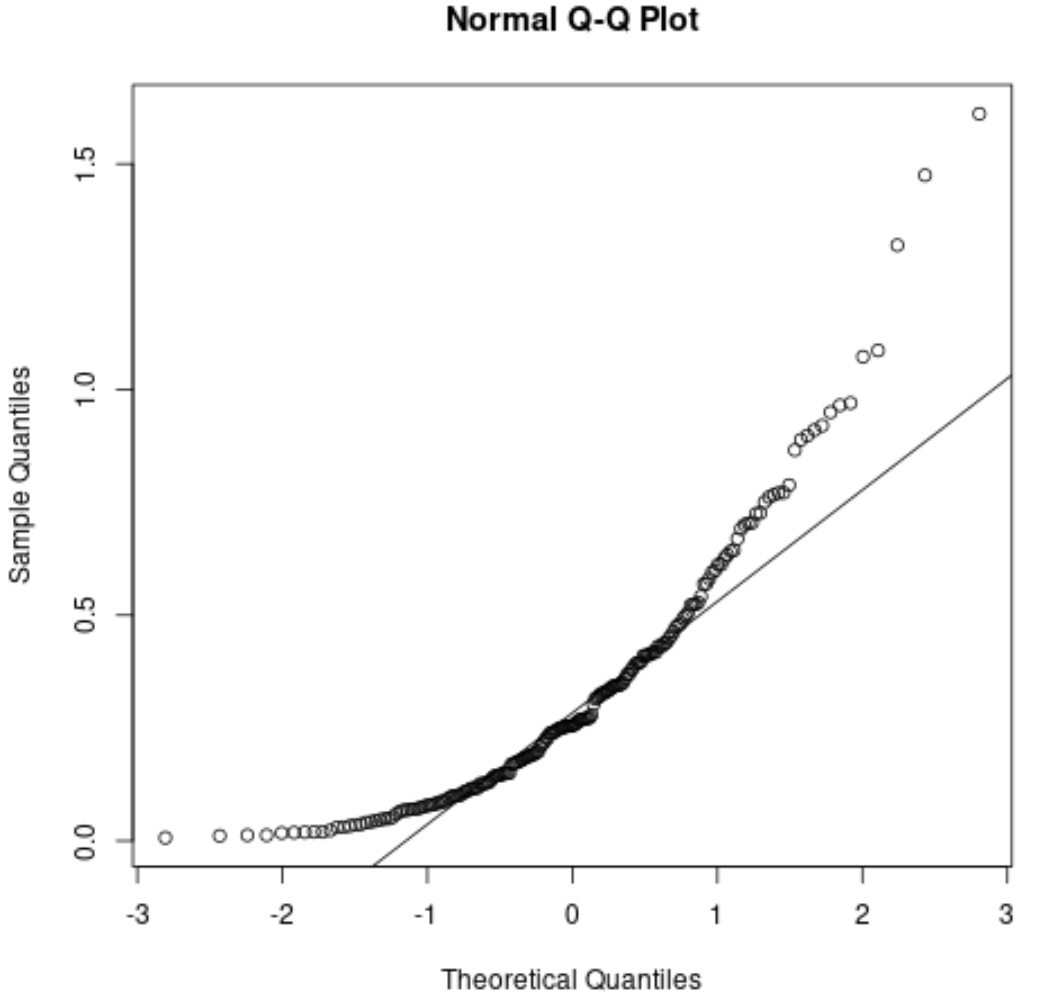
De punten wijken sterk af van de rechte diagonale lijn, wat aangeeft dat de residuen niet normaal verdeeld zijn.
Raadpleeg de volgende tutorials om te leren hoe u QQ-plots in verschillende software kunt maken:
Aanvullende bronnen
De volgende artikelen bieden aanvullende informatie over ANOVA-modellen:
Een inleiding tot One-Way ANOVA
Hoe u ANOVA-aannames kunt controleren
4 voorbeelden van het gebruik van ANOVA in het echte leven
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder