De normale verdeling

De normale verdeling is de meest voorkomende kansverdeling in de statistiek.

Normale verdelingen hebben de volgende kenmerken:

• Belvorm
• Symmetrisch
• Het gemiddelde en de mediaan zijn gelijk; beide bevinden zich in het centrum van de distributie
• Ongeveer 68% van de gegevens valt binnen één standaarddeviatie van het gemiddelde
• Ongeveer 95% van de gegevens valt binnen twee standaarddeviaties van het gemiddelde.
• Ongeveer 99,7% van de gegevens valt binnen drie standaarddeviaties van het gemiddelde.

De laatste drie punten staan bekend als de vuistregel , ook wel de 68-95-99,7-regel genoemd.

Gerelateerd: Vuistregel (oefenproblemen)

Hoe teken je een normale curve?

Om een normale curve te tekenen, moeten we het gemiddelde en de standaarddeviatie kennen.

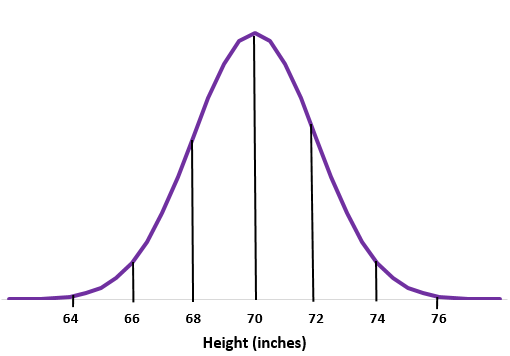
Voorbeeld 1: Stel dat de lengte van mannen op een bepaalde school normaal verdeeld is met een gemiddelde van $\mu =\; 70\; inch\; en$ een standaarddeviatie van $\sigma \; =\; 2\; inch.\; Schets\; de\; normale\; curve.$

Stap 1: Schets een normale curve.

Stap 2: Het gemiddelde van 70 inch ligt in het midden.

Stap 3: Elke standaardafwijking komt overeen met een afstand van 2 inch.

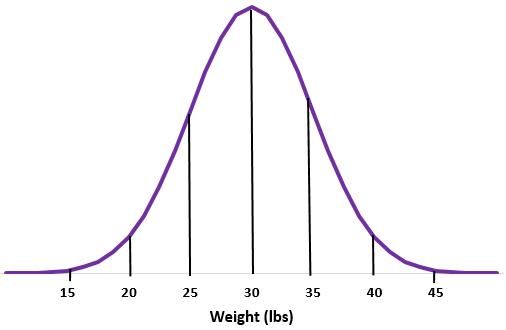
Voorbeeld 2: Stel dat het gewicht van een bepaalde ottersoort normaal verdeeld is met een gemiddelde van $\mu =\; 30\; lb\; en$ een standaarddeviatie van $\sigma \; =\; 5\; lb.\; Schets\; de\; normale\; curve.$

Stap 1: Schets een normale curve.

Stap 2: Het gemiddelde van 30 pond valt in het midden.

Stap 3: Elke standaardafwijking komt overeen met een afstand van 5 lbs

Hoe u percentages kunt vinden met behulp van de normale verdeling

De vuistregel , ook wel de 68-95-99.7-regel genoemd, stelt dat voor een normaal verdeelde willekeurige variabele 68% van de gegevens binnen een bereik van één standaardafwijking van het gemiddelde valt, en 95% binnen een bereik van twee standaardafwijkingen. afwijkingen van het gemiddelde en 99,7% liggen binnen drie standaardafwijkingen van het gemiddelde.

Met deze regel kunnen we vragen over percentages beantwoorden.

Voorbeeld: Stel dat de lengte van mannen op een bepaalde school normaal verdeeld is met een gemiddelde van $\mu =\; 70\; inch\; en$ een standaarddeviatie van $\sigma \; =\; 2\; inch.$

$Hoeveel\; procent\; van\; de\; mannen\; op\; deze\; school\; is\; ongeveer\; 220\; cm\; lang?$

Oplossing:

Stap 1: Schets een normale verdeling met een gemiddelde van $\mu =\; 70\; inch\; en$ een standaarddeviatie van $\sigma \; =\; 2\; inch.$

Stap 2: Een lengte van 74 inch is twee standaarddeviaties boven het gemiddelde. Voeg de percentages boven dit punt toe aan de normale verdeling.

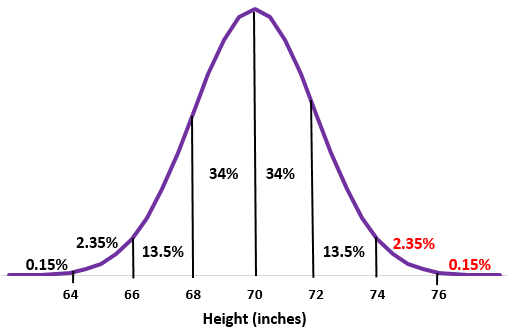
2,35% + 0,15% = 2,5%

Ongeveer 2,5% van de mannen op deze school is langer dan 220 cm.

$Hoeveel\; procent\; van\; de\; mannen\; op\; deze\; school\; is\; ongeveer\; tussen\; de\; 180\; en\; 180\; centimeter\; lang?$

Oplossing:

Stap 1: Schets een normale verdeling met een gemiddelde van $\mu =\; 70\; inch\; en$ een standaarddeviatie van $\sigma \; =\; 2\; inch.$

Stap 2: Een lengte van 68 inch en 72 inch is respectievelijk één standaardafwijking onder en boven het gemiddelde. Voeg eenvoudigweg de percentages tussen deze twee punten in de normale verdeling toe.

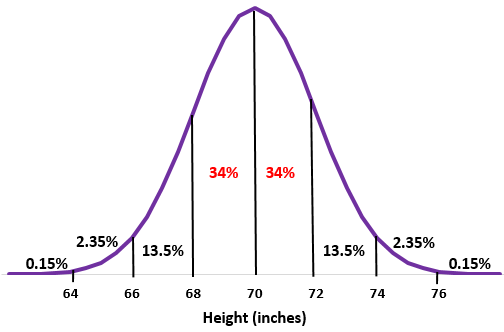
34% + 34% = 68%

Ongeveer 68% van de mannen op deze school is tussen de 180 en 180 centimeter lang.

Hoe u tellingen kunt vinden met behulp van de normale verdeling

We kunnen de vuistregel ook gebruiken om vragen over tellingen te beantwoorden.

Voorbeeld: Stel dat het gewicht van een bepaalde ottersoort normaal verdeeld is met een gemiddelde van $\mu =\; 30\; lb\; en$ een standaarddeviatie van $\sigma \; =\; 5\; lb.$

Een bepaalde kolonie heeft 200 van deze otters. Hoeveel van deze otters wegen ongeveer meer dan 35 pond?

Oplossing:

Stap 1: Schets een normale verdeling met een gemiddelde van $\mu =\; 30\; lb\; en$ een standaarddeviatie van $\sigma \; =\; 5\; lb.$

Stap 2: Een gewicht van 35 lbs is één standaardafwijking boven het gemiddelde. Voeg de percentages boven dit punt toe aan de normale verdeling.

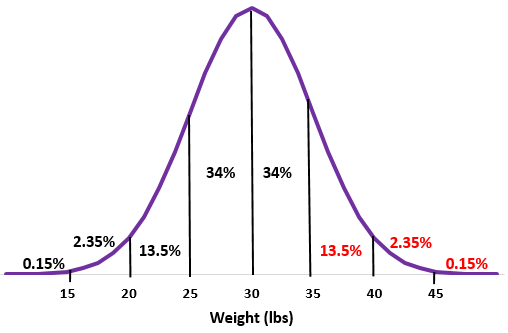
13,5% + 2,35% + 0,15% = 16%

Stap 3: Aangezien er 200 otters in de kolonie zijn, is 16% van 200 = 0,16 * 200 = 32

Ongeveer 32 otters in deze kolonie wegen meer dan 35 pond.

Hoeveel otters in deze kolonie wegen ongeveer minder dan 30 pond?

In plaats van alle stappen te volgen die we zojuist hierboven hebben genomen, kunnen we inzien dat de mediaan van een normale verdeling gelijk is aan het gemiddelde, dat in dit geval 30 pond is.

Dit betekent dat de helft van de otters meer dan 30 kilo weegt en de andere helft minder dan 30 kilo. Dit betekent dat 50% van de 200 otters minder dan 30 kilo weegt, dus 0,5 * 200 = 100 otters .

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over de normale verdeling:

6 concrete voorbeelden van de normale verdeling
Normale verdeling versus t-verdeling: het verschil
Hoe u een belcurve maakt in Excel
Hoe u een belcurve maakt in Python