Kan de variantie negatief zijn?

In de statistieken verwijst de term variantie naar hoe waarden worden verdeeld in een bepaalde dataset.

Een veel voorkomende vraag die studenten stellen over variantie is:

Kan de variantie negatief zijn?

Het antwoord: Nee, de variantie kan niet negatief zijn. De laagste waarde die deze kan aannemen is nul.

Om te begrijpen waarom dit het geval is, moeten we begrijpen hoe variantie feitelijk wordt berekend.

Hoe de kloof te berekenen

De formule voor het vinden van de variantie van een steekproef (aangeduid als s ² ) is:

s ² = Σ (x _ik – X ) ² / (n-1)

Goud:

• x : De steekproefgemiddelden
• x _i : De ^i-de waarneming in de steekproef
• N : Steekproefomvang
• Σ : Een Grieks symbool dat ‘som’ betekent

Stel dat we bijvoorbeeld de volgende gegevensset hebben met 10 waarden:

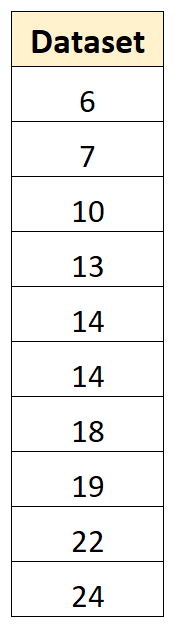
We kunnen de volgende stappen gebruiken om de variantie van dit monster te berekenen:

Stap 1: Zoek het gemiddelde

Het gemiddelde is gewoon het gemiddelde. Dit blijkt 14,7 te zijn.

Stap 2: Zoek de kwadratische afwijkingen

Vervolgens kunnen we de kwadratische afwijking van elke individuele waarde van het gemiddelde berekenen.

De eerste kwadratische afwijking wordt bijvoorbeeld berekend als (6-14,7) ² = 75,69.

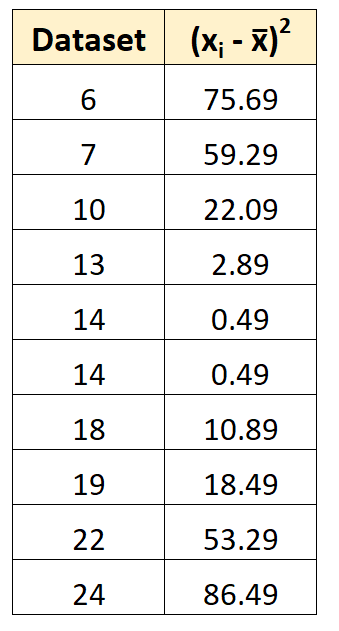
Stap 3: Vind de som van de gekwadrateerde afwijkingen

Dan kunnen we alle kwadraten van de afwijkingen optellen:

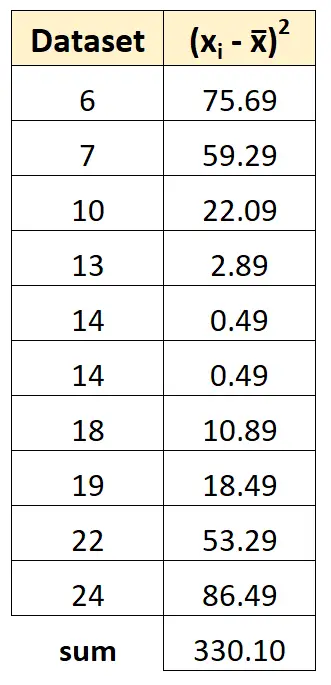
Stap 4: Bereken de steekproefvariantie

Ten slotte kunnen we de steekproefvariantie berekenen als de som van de kwadratische afwijkingen gedeeld door (n-1):

^s2 = 330,1 / (10-1) = 330,1 / 9 = 36,678

De steekproefvariantie blijkt 36.678 te zijn.

Een voorbeeld van nulvariantie

De enige manier waarop een dataset een variantie van nul kan hebben, is als alle waarden in de dataset hetzelfde zijn .

De volgende gegevensset heeft bijvoorbeeld een steekproefvariantie van nul:

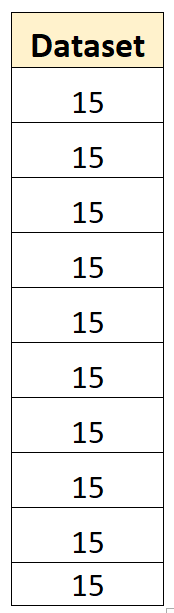
Het gemiddelde van de dataset is 15 en geen van de individuele waarden wijkt af van het gemiddelde. De som van de kwadraten van de afwijkingen zal dus nul zijn en de steekproefvariantie zal eenvoudigweg nul zijn.

Kan de standaarddeviatie negatief zijn?

Een meer gebruikelijke manier om de verdeling van waarden in een dataset te meten, is door de standaarddeviatie te gebruiken, wat simpelweg de wortel is van de variantie.

Als de variantie van een gegeven steekproef bijvoorbeeld ^s2 = 36,678 is, wordt de standaarddeviatie (geschreven s ) als volgt berekend:

s = √ ^s2 = √ 36,678 = 6,056

Omdat we al weten dat de variantie altijd nul of een positief getal is, betekent dit dat de standaarddeviatie nooit negatief kan zijn, aangezien de vierkantswortel van nul of een positief getal niet negatief kan zijn.

Aanvullende bronnen

Maatregelen van centrale tendens: definitie en voorbeelden
Verspreidingsmaatregelen: definitie en voorbeelden