Covariantiematrix

In dit artikel wordt uitgelegd wat de covariantiematrix is en wat de formule ervan is. Je ontdekt hoe je de covariantiematrix maakt met een concreet voorbeeld en de eigenschappen van covariantiematrices.

Wat is de covariantiematrix?

De covariantiematrix is een vierkante matrix waarvan de elementen de varianties en covarianties zijn van de bestudeerde variabelen. De elementen van de hoofddiagonaal van de covariantiematrix zijn dus de variantie van elke variabele, en de overige elementen zijn de covarianties tussen de variabelen.

In de statistiek wordt de covariantiematrix gebruikt om de relatie tussen twee of meer willekeurige variabelen te analyseren. De covariantiematrix is erg handig omdat je hiermee snel de correlatie tussen veel variabelen kunt interpreteren, omdat je de waarden van alle covarianties van de variabelen tegelijkertijd kunt zien.

Het symbool voor de covariantiematrix is de Griekse hoofdletter sigma (Σ).

Hoe de covariantiematrix te berekenen

Om de covariantiematrix van verschillende statistische variabelen te berekenen , moeten de volgende stappen worden uitgevoerd:

1. Bereken de varianties van alle variabelen.
2. Bereken de covariantie van elk paar variabelen.
3. Vorm de covariantiematrix:
• De variantie van de variabele i moet op de hoofddiagonaal van de matrix worden geplaatst, meer bepaald op positie i,i .
• De covariantie tussen variabelen i en j moet op positie i,j van de matrix worden geplaatst.

De formule voor de covariantiematrix is daarom als volgt:

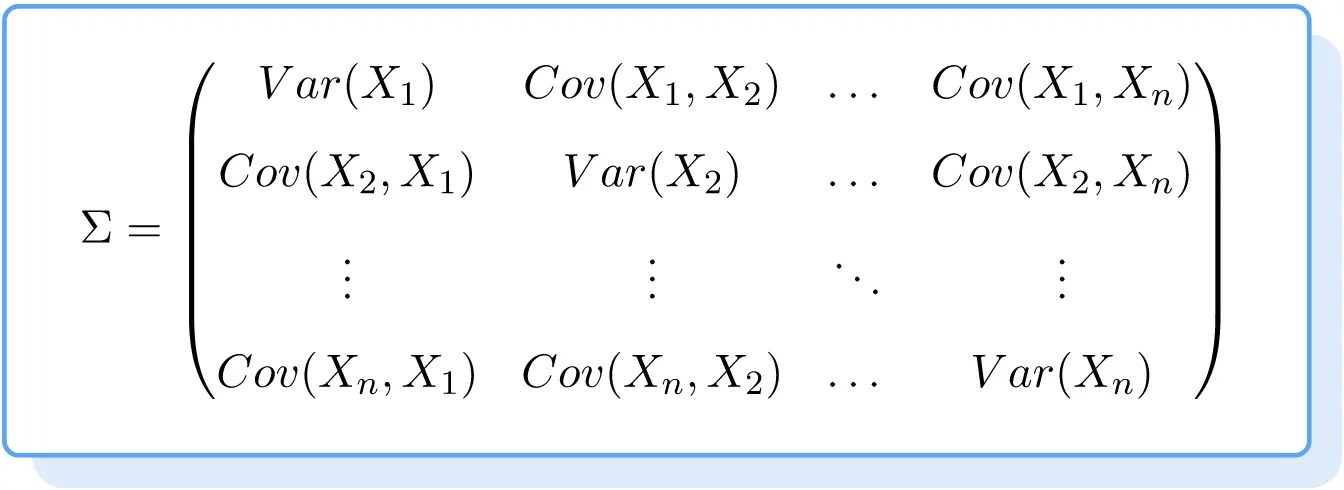
Voorbeeld van een covariantiematrix

Nadat u de definitie van covariantiematrix heeft gezien, vindt u hieronder een stapsgewijze oefening, zodat u kunt zien hoe dit type matrix wordt gemaakt.

Berekent de covariantiematrix van de variabelen X, Y en Z, waarvan de waarden zijn:

• X: 4, 7, 12, 5, 7
• En: 9, 15, 19, 6, 8
• Z: 7, 2, 4, 6, 3

Het eerste dat we moeten doen is de varianties van alle variabelen bepalen:

Ten tweede vinden we de covariantie tussen elk paar variabelen:

En zodra we alle varianties en covarianties hebben berekend, hoeft we alleen nog maar de covariantiematrix te maken. Om dit te doen, plaatsen we de variantiewaarden op de hoofddiagonaal van de matrix en de covariantiewaarden in hun overeenkomstige positie:

Zoals u kunt zien, is het heel eenvoudig om de variabelen te interpreteren door de varianties en covarianties in een matrix weer te geven. De variabele met de grootste spreiding is Y (23,44), aan de andere kant hebben de variabelen X en Y een directe relatie, terwijl de variabelen X en Z (en dus Y en Z) een omgekeerde relatie hebben.

Merk op dat de covariantiematrix altijd symmetrisch is, aangezien de covariantie tussen twee variabelen niet afhankelijk is van de volgorde van de variabelen. Bijvoorbeeld,

is gelijk aan

Bovendien zal de covariantiematrix altijd een vierkante matrix zijn en zal de dimensie ervan gelijk zijn aan het aantal variabelen. In dit geval hadden we drie variabelen en daarom is het een 3×3-matrix, maar als we maar twee variabelen hadden, zou de covariantiematrix 2×2 zijn geweest.

Eigenschappen van de covariantiematrix

De covariantiematrix heeft de volgende kenmerken:

• De covariantiematrix is een vierkante matrix in de orde van het aantal variabelen.
• De covariantiematrix is symmetrisch, wat betekent dat de hoofddiagonaal van de matrix een symmetrieas is.
• De covariantiematrix is altijd positief semi-definitief.
• De determinant van de covariantiematrix is gelijk aan of groter dan nul.