Monsteraandeel

In dit artikel wordt uitgelegd wat de steekproefaandeel in de statistiek is. Zo ontdek je hoe je de steekproefaandeel berekent, een opgeloste oefening en ook wat het verschil is tussen de steekproefaandeel en de populatieaandeel.

Wat is de steekproefverhouding?

Steekproefproportie is de verhouding tussen het aantal succesvolle cases in een steekproef en de steekproefomvang. Om de steekproefaandeel te berekenen, moet daarom het aantal successen in de steekproef worden gedeeld door het totale aantal gegevens.

Het symbool voor monsteraandeel is

.

In de statistiek zijn bij het uitvoeren van een enquête meestal niet alle populatiegegevens bekend. Daarom wordt meestal een onderzoek van een representatieve steekproef uitgevoerd, en vervolgens worden de getrokken conclusies geëxtrapoleerd naar de gehele populatie. bevolking. Het steekproefaandeel wordt dus gebruikt om het aandeel van de gehele populatie te schatten. Hieronder zullen we zien hoe dit wordt gedaan.

Voorbeeld van proportieformule

De steekproefaandeel is gelijk aan het aantal succesvolle gevallen in de steekproef gedeeld door de steekproefomvang. Daarom is de formule voor het berekenen van het steekproefaandeel :

Goud:

• 

  is de steekproefaandeel.

• 

  is het aantal succesvolle gevallen in de steekproef.

• 

  is het totale aantal gegevensitems in de steekproef.

Voorbeeld van berekening van monsteraandeel

Nadat we de definitie van steekproefaandeel hebben gezien en wat de formule ervan is, zullen we in deze sectie een eenvoudig voorbeeld oplossen, zodat u kunt zien hoe steekproefaandeel wordt berekend.

• Een bedrijf vervaardigt speelgoed en koopt een onderdeel ervan van een ander extern bedrijf. Binnen de batches die hij koopt, komen er echter defecte onderdelen voor, dus besluit hij een statistisch onderzoek uit te voeren om het aandeel onderdelen in goede staat en het aandeel defecten te achterhalen. U bestelt dus een monster van 1.000 eenheden en vindt 138 defecte onderdelen. Wat is het aandeel onderdelen in goede staat in het monster? En wat is het aandeel defecte onderdelen in het monster?

Het aantal onbeschadigde onderdelen in het monster is 1000 minus het aantal defecte onderdelen:

Om de steekproefverhouding te vinden, passen we dus de formule toe die we hierboven hebben gezien:

Het aandeel van het monster met onderdelen in goede staat bedraagt dus 86,2%.

Aan de andere kant is het aandeel defecte onderdelen gelijk aan één minus het aandeel goede onderdelen:

Het monsteraandeel defecte onderdelen bedraagt daarom 13,8%.

Steekproefaandeel en populatieaandeel

Het bevolkingsaandeel is het aandeel van de statistische populatie. Dat wil zeggen dat de populatieaandeel de relatie is tussen de succesgevallen van een bestudeerde populatie in relatie tot alle elementen die deel uitmaken van die populatie.

Daarom is het verschil tussen het nationale aandeel en het bevolkingsaandeel dat het nationale aandeel het aandeel van de gevallen van een meerderheid is. In verandering verwijst het bevolkingsaandeel naar het aandeel gevallen van gebeurtenissen die alle elementen van de bevolking respecteren.

Om het steekproefaandeel te onderscheiden van het populatieaandeel, worden ze weergegeven door verschillende symbolen. Het symbool voor monsteraandeel is

, terwijl het symbool voor bevolkingsaandeel is

.

Over het algemeen kan het bevolkingsaandeel niet precies worden bepaald, omdat meestal niet alle populatiewaarden bekend zijn. In plaats daarvan wordt de waarde van het populatieaandeel gewoonlijk geschat met behulp van een betrouwbaarheidsinterval met de volgende formule:

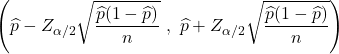
Om te zien hoe het bevolkingsaandeel wordt geschat, klikt u op de volgende link:

Bemonsteringsverdeling van verhoudingen

Ten slotte zullen we zien waaruit een steekproefverdeling van proporties bestaat, aangezien het een statistisch concept is dat verband houdt met de steekproefproportie.

Laten we eerst beginnen met te definiëren wat een steekproefverdeling is. Een steekproefverdeling is de verdeling die het resultaat is van het in aanmerking nemen van alle mogelijke steekproeven uit een statistische populatie.

Daarom is een steekproefverdeling van verhoudingen de verdeling die het resultaat is van de berekening van het aandeel van elke mogelijke steekproef uit een populatie. Dat wil zeggen, als we alle mogelijke steekproeven uit een populatie bestuderen en het aandeel van elk van de steekproeven berekenen, is de berekende reeks waarden een steekproefverdeling van steekproefverhoudingen.