Bepalingscoëfficiënt (r kwadraat)

Von Dr.benjamin anderson August 2, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat de determinatiecoëfficiënt (of R-kwadraat) is in de statistiek. U leert dus hoe u de determinatiecoëfficiënt kunt berekenen, hoe deze wordt geïnterpreteerd en bovendien een online calculator om de determinatiecoëfficiënt van een gegevensmonster te berekenen.

Wat is de determinatiecoëfficiënt (R kwadraat)?

De determinatiecoëfficiënt , waarvan het symbool R ² ( R kwadraat ) is, is een statistiek die de geschiktheid van een regressiemodel meet. De determinatiecoëfficiënt laat zien hoe goed een regressiemodel bij een dataset past, dat wil zeggen, het geeft het percentage aan dat door het regressiemodel wordt verklaard.

Hoe hoger de determinatiecoëfficiënt, hoe beter het regressiemodel. Hoewel niet altijd aan deze voorwaarde wordt voldaan, zijn wij in principe geïnteresseerd in een zo groot mogelijke determinatiecoëfficiënt. Hieronder zullen we zien hoe we de determinatiecoëfficiënt moeten interpreteren.

Formule voor het bepalen van de coëfficiënt

De determinatiecoëfficiënt is gelijk aan één minus de verhouding tussen de resterende variantie en de variantie van de afhankelijke variabele. De determinatiecoëfficiënt kan ook worden berekend door één minus de kwadratensom af te trekken van de residuen over de totale som van de kwadraten.

De formule voor het berekenen van de determinatiecoëfficiënt is dus als volgt:

formule voor determinatiecoëfficiënt, formule voor r kwadraat

Goud:

$R^2$

is de determinatiecoëfficiënt.
$\sigma_r^2$

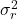
is de resterende variantie.
$\sigma^2$

is de variantie van de afhankelijke variabele Y.
$y_{i}$

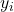
is de waarde van de observatie-afhankelijke variabele i.
$\widehat{y}_{i}$

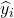
is de waarde benaderd door het regressiemodel voor observatie i.
$\overline{y}$

is het gemiddelde van de afhankelijke variabele voor alle waarnemingen.

👉 U kunt de onderstaande rekenmachine gebruiken om de determinatiecoëfficiënt voor elke dataset te berekenen.

Voor het lineaire regressiemodel is de determinatiecoëfficiënt gelijk aan het kwadraat van de correlatiecoëfficiënt :

$R^2=\cfrac{\sigma_{XY}^2}{\sigma_X^2\sigma_Y^2}=\rho^2$

Goud

$\sigma_{XY}^2$

is de covariantie van de variabelen X en Y,

$\sigma_X^2$

$\sigma_Y^2$

zijn de varianties van respectievelijk de onafhankelijke variabele X en de afhankelijke variabele Y.

Bepalingscoëfficiëntcalculator

Sluit een voorbeeldgegevens aan op de onderstaande rekenmachine om een eenvoudig lineair regressiemodel in te passen en de determinatiecoëfficiënt ervan te berekenen. U moet de gegevensparen scheiden, zodat in het eerste vak alleen de waarden van de onafhankelijke variabele X staan en in het tweede vak alleen de waarden van de afhankelijke variabele Y.

Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Interpretatie van de determinatiecoëfficiënt

In dit gedeelte zullen we zien hoe we de determinatiecoëfficiënt moeten interpreteren, omdat het geen zin heeft om de waarde van de determinatiecoëfficiënt te kennen als je later niet weet wat het betekent.

De waarde van de determinatiecoëfficiënt kan variëren van 0 tot 1, maar wordt meestal uitgedrukt als een percentage, dus het minimum is 0% en het maximum is 100%.

Wat de interpretatie van de determinatiecoëfficiënt betreft: hoe hoger de waarde ervan, betekent dat het regressiemodel de gegevenssteekproef beter verklaart. Dus hoe dichter de determinatiecoëfficiënt bij 1 ligt, hoe meer het model zal worden aangepast. Aan de andere kant geldt dat hoe dichter de waarde bij 0 ligt, hoe minder betrouwbaar het geproduceerde regressiemodel zal zijn.

Bij het vergelijken van twee regressiemodellen is het model met een hogere regressiecoëfficiënt echter niet altijd beter. Een regressiemodel kan bijvoorbeeld een regressiecoëfficiënt R ² = 100% hebben, omdat er veel verklarende variabelen aan het model zijn toegevoegd en het daarom alle waarnemingen perfect kan verklaren. Maar dit model doet zeker een zeer slechte voorspelling voor een nieuwe waarde die niet werd gebruikt om het regressiemodel te bouwen.

Er moet ook rekening mee worden gehouden dat het resulterende regressiemodel aan de voorgaande aannames voldoet. Een model met een zeer hoge determinatiecoëfficiënt is dus nutteloos als de variabiliteit van de residuen niet constant is (homoscedasticiteit).

Bovendien vormt de determinatiecoëfficiënt een belangrijke grens, aangezien deze de opname van verklarende variabelen niet bestraft. Logischerwijs geldt dat hoe meer verklarende variabelen een regressiemodel heeft, hoe complexer het model zal zijn, maar hoe beter het de waargenomen gegevens zal verklaren en dus hoe hoger de determinatiecoëfficiënt. De aangepaste determinatiecoëfficiënt houdt echter rekening met het aantal variabelen in het model (we zullen hieronder zien hoe deze wordt berekend).

Concluderend is de determinatiecoëfficiënt zeer nuttig voor het analyseren van een regressiemodel, omdat deze ons laat weten hoe goed het regressiemodel bij de dataset past. Er moeten echter ook andere hulpmiddelen worden gebruikt om het resulterende model te beoordelen, zoals statistische grafieken .

Aangepaste bepalingscoëfficiënt

De aangepaste determinatiecoëfficiënt , ook wel de aangepaste determinatiecoëfficiënt genoemd, meet de goodness of fit van een regressiemodel door rekening te houden met het aantal verklarende variabelen dat in het model is opgenomen.

Het verschil tussen de determinatiecoëfficiënt en de aangepaste determinatiecoëfficiënt is dat de determinatiecoëfficiënt de kwaliteit van de aanpassing meet zonder rekening te houden met het aantal variabelen. De aangepaste determinatiecoëfficiënt meet daarentegen de kwaliteit van de aanpassing straffen voor elke toegevoegde variabele.

De formule voor het berekenen van de aangepaste determinatiecoëfficiënt is als volgt:

$\bar{R}^2=1-\cfrac{N-1}{N-k-1}\cdot (1-R^2)$

Goud:

$\bar{R}^2$

is de aangepaste determinatiecoëfficiënt.
$R^2$

is de determinatiecoëfficiënt.
$N$

is de steekproefomvang.
$k$

is het aantal verklarende variabelen in het regressiemodel.

Daarom is de aangepaste determinatiecoëfficiënt beter dan de determinatiecoëfficiënt voor het vergelijken van twee verschillende modellen, aangezien de modellen een verschillend aantal verklarende variabelen kunnen hebben.

➤ Zie: Aangepaste bepalingscoëfficiënt

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder