Hoe dfbetas in r te berekenen

In de statistiek willen we vaak weten welke invloed verschillende observaties hebben op regressiemodellen.

Eén manier om de invloed van waarnemingen te berekenen is door een metriek te gebruiken die bekend staat als DFBETAS , die ons het gestandaardiseerde effect op elke coëfficiënt vertelt van het verwijderen van elke individuele waarneming.

Deze metriek geeft ons een idee van de invloed van elke waarneming op elke coëfficiëntschatting in een bepaald regressiemodel.

Deze tutorial toont een stapsgewijs voorbeeld van hoe u DFBETAS voor elke waarneming in een model in R kunt berekenen en visualiseren.

Stap 1: Maak een regressiemodel

Eerst zullen we een meervoudig lineair regressiemodel maken met behulp van de mtcars- dataset die in R is ingebouwd:

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Stap 2: Bereken DFBETAS voor elke waarneming

Vervolgens zullen we de ingebouwde functie dfbetas() gebruiken om de DFBETAS-waarden voor elke waarneming in het model te berekenen:

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

Voor elke waarneming kunnen we het verschil zien in de coëfficiëntschatting voor de oorsprong, de disp- variabele en de hp- variabele die optreedt wanneer we die specifieke waarneming verwijderen.

Over het algemeen zijn we van mening dat een waarneming een sterke invloed heeft op de schatting van een bepaalde coëfficiënt als deze een DBETAS-waarde heeft die groter is dan een drempelwaarde van 2/√ n , waarbij n het aantal waarnemingen is.

In dit voorbeeld zou de drempel 0,3535534 zijn:

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

Stap 3: Visualiseer de DFBETAS

Ten slotte kunnen we grafieken maken om de DFBETAS-waarde voor elke waarneming en voor elke voorspeller in het model te visualiseren:

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

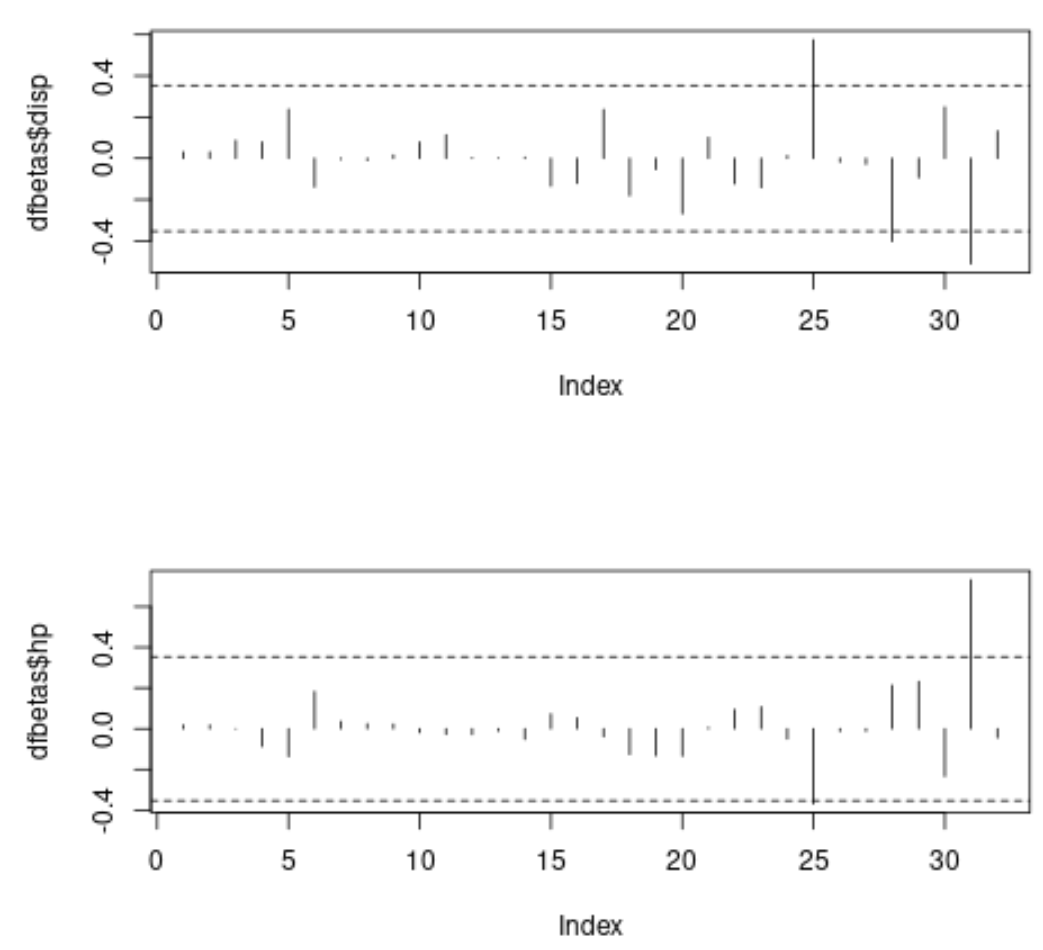
In elke plot geeft de x-as de index van elke waarneming in de dataset weer en geeft de y-waarde de overeenkomstige DFBETAS weer voor elke waarneming en elke voorspeller.

Op de eerste grafiek kunnen we zien dat drie waarnemingen de absolute drempelwaarde van 0,3535534 overschrijden en op de tweede grafiek kunnen we zien dat twee waarnemingen de absolute drempelwaarde overschrijden.

We kunnen ervoor kiezen deze waarnemingen nader te bestuderen om te bepalen of ze een overmatige invloed hebben op de schatting van de modelcoëfficiënten.

Aanvullende bronnen

Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe u hefboomstatistieken kunt berekenen in R
Hoe DFFITS in R te berekenen